Для расчета надежности комбинированных систем целесообразно предварительно произвести декомпозицию системы, разбив ее на простые подсистемы – группы элементов, методика расчета надежности которых известна. Затем эти подсистемы в структурной схеме надежности заменяются элементами (квазиэлементами) с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем. При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока не получится структура, методика расчета надежности которой известна.
В качестве примера рассмотрим комбинированную систему, представленную на рис. 1.15. Здесь элементы (2 и 5), (4 и 7), (9 и 12), (11 и 14) попарно образуют друг с другом последовательные соединения. Заменим их соответственно элементами А, В, С, D, для которых расчет надежности рассматривался ранее.
Элементы 15, 16, 17 и 18 образуют параллельное соединение, а элементы 3, 6, 8, 10 и 13 – систему “3 из 5”. Соответствующие элементы обозначим E и F. В результате преобразованная схема примет вид, показанный на рис. 1.16, а. В ней в свою очередь элементы А, В, С, D, F образуют мостиковую схему, которую заменяем элементом G.
| 
|
| Рис. 1.15. Исходная система | Рис. 1.16..Преобразованные системы |
После таких преобразований получается последовательная система, состоящая из элементов 1, G, E, 19 (рис. 1.16, б).
Порядок выполнения работы
1. Обучающиеся совместно с преподавателем решают пример по условиям задачи 1.
ЗАДАЧА 1
Условие. Двигатель легкового автомобиля имеет 4 свечи зажигания, по одной на каждый цилиндр. Интенсивность отказов свечи l = 10-3 1/ч, а длительность работы двигателя в течение всего маршрута t = 20 ч. Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Какова вероятность того, что автомобиль доставит пассажиров в пункт назначения без замены свечей?
Решение. Благоприятные ситуации, не приводящие к отказу двигателя в целом возникают в том случае, если:
1. А – за время t ни одна из свечей не отказала;
2. Б – отказала одна свеча, проработав время t < t, при этом 3 остальные остались исправными в течение времени t.
3. Вероятность того, что не откажет ни одна свеча будет равна произведению вероятностей p(t) безотказной работы всех четырех свечей, т.е. PА(t) = p4(t).
4. Вероятность того, что три свечи исправны, а одна нет, равна p3q.
5. Так как в цилиндрах четыре свечи, то возможен выход из строя любой из них, поэтому вероятность гипотезы Б
PБ(t) = C14 p3(t)q(t) = 4p3(t)(1-p(t)).
6. Коэффициент C14 имеет место, поскольку может отказать любая свеча (одна из четырех).
7. Суммируя вероятности гипотез А и Б, получим
PС(t) = PА(t) + PБ(t) = p4(t) + 4p3(t)(1-p(t)) = p3(t)[p(t) + 4(1-p(t)].
8. Имея в виду, что p(t) = exp(-lt), то очевидно, что
PС = exp(-3 l t)[exp(- l t) + 4(1- exp(- l t)] =0,996
2. Обучающиеся индивидуально, разрабатывают функциональную модель по условиям задачи 2, считая все устройства отдельными элементами. Преподаватель контролирует и помогает в составлении схем.
ЗАДАЧА 2
Условие. Система смазки двигателя ЯМЗ-238 состоит из следующих элементов: масляного поддона, сетчатого заборника, масляного насоса, фильтра грубой очистки, фильтра центробежной очистки масла (неполнопоточная центрифуга), центрального масляного канала, масляного радиатора и клапанов.
В результате анализа функционирования системы смазки двигателя, выделено три возможные причины отказа; отказ вследствие чрезмерного давления масла в системе после масляного насоса, отказ при работе с загрязненным фильтром грубой очистки, отказ из-за высокого давления в масляном радиаторе. Остальные элементы приняты абсолютно надежными. В конструкции для повышения безотказности предусмотрены следующие предохранительные элементы:
- в масляном насосе для поддержания необходимого давления масла в нагнетательной секции насоса предусмотрен редукционный клапан, который открывается при давлении масла более 0,7 МПа и масло из полости нагнетания перепускается во всасывающую полость;
- в корпусе фильтра грубой очистки масла установлен предохранительный клапан, который, в случае сильного засорения фильтрующего элемента, открывается при достижении давления 0,2 Мпа и масло поступает в центральный масляный канал, минуя фильтр, что предохраняет подшипники двигателя от перегрева из-за недостатка масла;
- необходимое давление масла, создаваемое радиаторной секцией насоса при нагнетании масла в радиатор, поддерживается перепускным клапаном, который при увеличении давления более 0,08 МПа открывается, и масло из полости нагнетания перепускается во всасывающую полость насоса.
3. Обучающиеся получают от преподавателя задание для самостоятельного решения задач по расчету безотказности систем по структурным схемам, приведенным в приложении 3 и значениям показателей надежности, приведенным в приложении 4.
Содержание отчета
1. Решение задачи 1.
2. Разработанная функциональная модель по условиям задачи 2.
3. Самостоятельно решенное индивидуальное задание по исходным данным приложений 3, 4.
Вопросы для самостоятельной работы
1. Что такое отказ?
2. Дать понятие вероятности безотказной работы
3. Дать понятие вероятности отказа
4. Что такое наработка?
5. Какова зависимость между вероятностью безотказной работы объекта и его средней наработкой до отказа?
6. Как связаны между собой вероятность безотказной работы и интенсивность отказов объекта?
7. Что понимается под g-процентной наработкой?
8. Каким образом выглядит соотношение между плотностью распределения и интенсивностью отказов при экспоненциальном законе распределения наработки объекта до отказа?
9. Что значит «рассчитать систему на надежность»?
10. Каковы аналитические соотношения расчета надежности при основном соединении элементов, последовательном, системы “ m из n “, мостиковых, комбинированных?
11. Каковы недостатки основного соединения элементов в системе?
12. Что такое резервирование?
13. Как оценивается выигрыш надежности при резервировании?
14. Что такое минимальное сечение?
15. Что такое минимальный путь?
16. Что подразумевается под квазиэлементами?
Лабораторная работа №3
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ
Цель работы: Ознакомиться с основными инструментами и приборами для измерений, научиться вычислять ошибки измерений, изучить методику обработки экспериментальных данных о параметрах технического состояния машины, уметь определять законы распределения графическим способом.
Задачи работы:
1. Ознакомиться с основными инструментами и приборами для измерений, научиться вычислять ошибки измерений.
2. Знать правила подготовки исходных данных и методику определения законов распределения графическим способом.
3. Уметь проводить измерения различными инструментами с разной погрешностью измерений, оценивать ошибки измерений и определять законы распределения экспериментальных данных графическим способом.
Теоретическая часть
Измерение – процесс сравнения данной величины с ее значением, принятым за единицу.
Основные тенденции в развитии способов измерений: повышение точности измерений; переход к измерениям микровеличин; применение приборов безынерционных и без трения или, по крайней мере, с величинами сил инерции и трения, которыми практически можно пренебречь; применение бесконтактных приборов; регистрация непрерывно изменяющихся величин; уменьшение затрат времени и труда на производство измерений.
Измеряемые величины, основные инструменты и приборы для измерений представлены в табл. 1.1. При неоднократных измерениях изменяющихся величин лучше употреблять считающие или записывающие приборы и устройства.
В случае функционального анализа связей между несколькими переменными требуется синхронная запись их значений. Например, надо установить зависимость нагрузки на вал кривошипа от угла поворота вала.
Очевидно, что для этого необходимо знать значения нагрузки и угла поворота вала в каждое данное мгновенье, т.е. синхронно записывать одновременно изменяющиеся переменные величины.
Таблица 1.1
Измеряемые величины и основные приборы для измерений
| Определяемые величины | Аппаратура |
| Геометрические: длина, высота, глубина, ширина, профили, площади, объемы | Мерительные ленты, линейки, щупы, штангенинструменты, светодальнометры, микрометры, нутрометры, глубинометры, миниметры, оптиметры, интерферометры, индикаторы, проекторы, микроскопы, планиметры, тензометры, счетчики объемов, пневматические и электрические измерительные приборы |
| Кинематические: скорость, ускорение, колебание, повторяемое движение | Измерители пути (угла поворота) и времени, измерители линейной и угловой скорости, тахометры, счетчики оборотов, ускорениеметры, вибрографы |
| Динамические: масса, импульс, сила, работа, момент, мощность | Весы, импульсометры, динамометры, тормозные устройства, манометры, барометры, индикаторы, работометры, специальные датчики и регулирующие устройства |
| Некоторые другие величины: время, световые величины, цвет, температура, электрические, химические и структурные свойства жидких и газообразных тел, излучение, звуковые величины | Часы, секундомеры, вибрационные и электронные устройства, фотометры, люксметры, термометры, термоэлементы, омметры, вольтметры, гальванометры, твердометры, оптические микроскопы, шумометры, звукоанализаторы |
Существуют три метода синхронной записи нескольких переменных величин: при помощи осциллографа, запись на магнитную ленту, киносъемка. При наиболее сложных явлениях протекания различных переменных регистрацию производят синхронно тремя или двумя этими способами.
Точность измерений [18]
Чем выше точность измерений, тем надежнее результаты исследований.
Точность – степень соответствия результата измерений действительному значению величины. Понятие точности связано с понятием ошибки: чем выше точность, тем меньше ошибка, и наоборот. Самые точные приборы не могут показать действительного значения величины, и их показания содержат ошибку.
Абсолютная ошибка – это разность между действительным значением измеряемой величины и ее наблюдаемым значением.
Практически под абсолютной ошибкой понимают разность между результатом измерения при помощи приборов высшей точности (образцовых) и значением этой же величины, полученным прибором, применяемым в исследованиях:
. (1.42)
Иногда под точностью понимают значение абсолютной сшибки.
Можно сказать, например, что точность измерения данным инструментом равна 0,01 мм. Чаще под точностью измерения понимают безразмерную величину или отношение абсолютной ошибки к действительному значению величины (это отношение иначе называется относительной ошибкой):
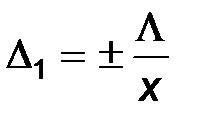(1.43)
или выражают ее в % к действительному значению величины:
. (1.44)
Для современных способов измерений можно считать, что величина незначительна в сравнении как с действительным значением х величины, так и с наблюдаемым при помощи точных (образцовых) приборов (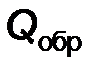
– значение). Считаясь с тем, что мы не можем измерить действительное значение х, выразим точность так:
; (1.45)
. (1.46)
Так, например, если 
мм и 
мм, то точность измерения 
.
Систематическими называются такие ошибки, которые возникают из-за известных причин, действующих по определенным законам и, как правило, в определенных направлениях.
Случайными ошибками называются те, причина которых неизвестна и которые невозможно учесть заранее. Такие ошибки характеризуют точность измерения. Суммарную случайную ошибку вычисляют на основании теории ошибок.
Часто применяют понятие предельной ошибки, под которой подразумевают наибольшую случайную ошибку при правильном Пользовании исправным прибором и устранении систематических ошибок при внесении соответствующих поправок, т.е. число 
, при котором 
.
При определении величины случайных ошибок, кроме предельной ошибки, вычисляют статистическую ошибку неоднократных измерений.
Если, например, диаметр вала, вязкость масла и т.д. измерять по одному разу, случайные ошибки могут сильно исказить результат. Поэтому лучше измерять какую-либо величину в тождественных условиях несколько раз и брать среднюю арифметическую этих измерений.
Рассеяние результатов измерений указывает на большую или меньшую их изменчивость и обычно оценивается средним квадратом отклонений наблюдаемых значений величины 
, от их средней или квадратным корнем из среднего квадрата.
Средняя арифметическая 
равна сумме всех взятых n отдельных результатов измерений 
, деленной на количество измерений:
. (1.47)
Если же все измерения сгруппированы в m классов с различным количеством измерений 
в каждом классе, то следует вычислять взвешенную арифметическую:
, (1.48)
где 
–средние по классу.
Отклонение любого отдельного результата измерений от средней арифметической можно представить как разность 
, где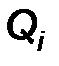 
– результат любого отдельного измерения.
Дисперсией случайной величины называется среднее значение квадрата отклонений случайной величины от ее среднего значения. Дисперсия обозначается через s2 и выражается формулой
. (1.49)
Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратическим отклонением, или стандартом;
. (1.50)
Коэффициентом вариации называется отношение среднего квадратического отклонения к среднеарифметическому значению результатов измерения:
. (151)
При измерении неизменной величины среднее квадратическое отклонение (стандарт) является мерой точности среднего арифметического значения неоднократно измеренной неизменной величины.
Если же неоднократно измеренная величина переменна, то вычисленное по ее измерениям значение стандарта показывает не только меру точности как случайную ошибку измерений, но и меру изменчивости переменной.
Для подавляющего большинства технических измерений можно считать, что наибольшей ошибкой средней арифметической многократных измерений является абсолютная величина, равная плюс-минус трем стандартам:
. (1.52)
или относительная величина:
; (1.53)
. (1.54)
Эту ошибку называют наибольшей возможной статистической в отличие от предельной ошибки.
Точность разных измерений оценивают по предельной ошибке. При неоднократных измерениях до их начала следует пользоваться предельной ошибкой (для подбора аппаратуры и представления о возможностях измерений), а после измерений оценивать их точность по наибольшей статистической ошибке.
Методика определения показателей надежности на основе законов распределения [19, 21]
Прежде чем приступить к рассмотрению методики как практически определить тот или иной закон распределения на основе имеющихся статистических данных о случайной величине, необходимо четко установить, что значит определить закон распределения. Под определением закона распределения случайной величины следует понимать решение двух основных задач:
1. На основе имеющихся статистических (экспериментальных) данных необходимо доказать графическим или расчетным способом, что они подчиняются тому или иному теоретическому закону распределения.
2. Определить численные значения параметров полученного закона распределения.
После получения (определения) закона распределения случайной величины производится оценка показателей надежности. При этом под „оценкой" понимаются две оценки: точечная и интервальная.
Порядок определения закона распределения аналитическим (расчетным) способом (с использованием гистограммы) устанавливается ГОСТ 11.006-74. Этот способ предусматривает определение плотности распределения 
различных законов.
Графическим способом (на основе вероятностных сеток) в настоящее время можно определять только следующие четыре закона: экспоненциальный (
), нормальный (
), Вейбулла (
) и логарифмически-нормальный (
). В этом случае определяется функция распределения 
.
Определение законов распределения с использованием графического способа производится в следующей последовательности:
- построение бланков вероятностных сеток;
- составление вариационного ряда на основе имеющихся статистических (экспериментальных) данных и вычисление статистической функции распределения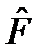 
(Х);
- нанесение исходной информации (координат 
и 
), имеющейся в вариационном ряду, на вероятностную сетку;
- аппроксимация (проведение прямой линии) нанесенной на вероятностную сетку исходной информации;
- проверка согласия статистического распределения с теоретическим по критерию Колмогорова;
- точечная оценка параметров полученного закона распределения.
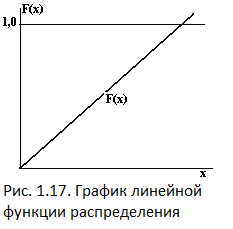
Идея применения вероятностных сеток для определения законов распределения случайных величин сводится к тому, чтобы предполагаемую функцию распределения F(Х) изобразить графически в виде прямой линии (рис. 1.17).
Эту идею можно осуществить для функций, которые имеют основание натурального логарифма е (ехр). Например, для экспоненциального закона имеем 
или 
. Прологарифмировав правую и левую части этого закона, получим: 
.
В результате этого логарифмирования получено уравнение прямой, для которой ордината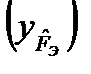 
является неравномерной (логарифмической), а абсцисса (Х) - равномерной. Задаваясь величиной 
от 0 до 1,0 и выбрав определенную высоту ординаты (например, 297мм»300мм, формат А4), можно рассчитать масштаб ординаты 
.
На оси абсцисс (X) вероятностной сетки (см. рис. 1.18) откладываются значения случайной величины .
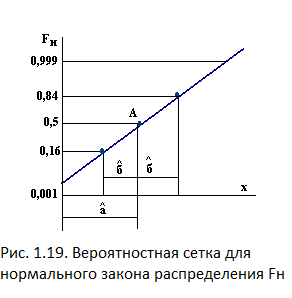
Для экспоненциального и нормального распределения (рис. 1.18, 1.19) строится равномерная шкала в масштабе и размерности случайной величины X.
Для законов Вейбулла (рис. 1.20) и логарифмически-нормального используется одинаковая неравномерная логарифмическая шкала по оси абсцисс с масштабом десятичных логарифмов и размерностью случайной величины lg X.
После построения вероятностных сеток производится подготовка исходных данных, необходимых для нанесения на вероятностные сетки.
Для этого составляется вариационный ряд (табл. 1.2), в котором случайные величины распределяют в возрастающем порядке.
В эту же таблицу заносят и значения эмпирической функции 
, определяемой по формулам:
или 
(1.55).
Эти формулы равнозначны, на практике используют любую из них, исходя из удобства вычислений. Если два и более элементов выборки в вариационном ряду совпадают (
), то для всех этих точек значение полагают равным последней точке (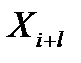
).
Таблица 1.2
Вариационный ряд
| 
| 
| ¼ | 
| 
| 
|
| i | ¼ | i | n-1 | n | ||
| 
| 
| ¼ | 
| 
| 
|
| 
| 
| ¼ | 
| 
| 
|
Рассмотренный способ построения вариационного ряда применяется для малых объемов выборок (п < 50).
При больших объемах выборки (п > 50) рекомендуется применять группировку исходных данных (X i). Через Хmin и Хmaх обозначают соответственно наименьший и наибольший элементы выборки. Затем выбирают округленные числа 
и 
, так, чтобы соблюдалось условие 
. Указанные числа 
и 
выбирают так, чтобы обеспечивалось разбиение интервала 
на равное (без остатка) количество интервалов К. При этом число интервалов К выбирается на основе рекомендаций, приведенных в табл. 1.3.
Таблица 1.3
Определение числа интервалов К
| Объем выборки | Число интервалов |
| 50< n <100 | 10--15 |
| 100< n <200 | 15--8 |
| n =200 | 18-20 |
| n =400 | 25-30 |
| n =1000 | 35-40 |
После определения числа интервалов размах L разбивают на интервалы (табл. 1.4) одинаковой величины h по формуле
. Число точек в i-м интервале (
) обозначают 
. Их должно быть не менее 5, т. е. >5 (i =1, 2, 3... К).
Количество точек в каждом интервале подсчитывают по следующим правилам:
1. Точка 
(первая точка в первом интервале) принимается за 0,5 точки.
2. Если точка X i находится на границе интервалов, то ее делят пополам и по 0,5 точки относят в смежные hi и hi+1 интервалы.
Возможны случаи, когда на границе интервалов находится не одна, а несколько точек. В этих случаях все точки делятся пополам и их половины распределяются по смежным интервалам.
При неравномерном распределении точек в интервалах возможны случаи, когда не выполняется условие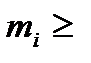 
5. В этих случаях допускается объединение соседних интервалов, в которых 
< 5. После объединения интервалы обозначаются hj, а число точек в каждом из j -х интервалов - 
.
| Таблица 1.4 Группировка статистических данных по интервалам | ||||||
| Интервалы
| Интервалы группировки, мм | Число точек
| Объединенные интервалы 
| Число точек 
|  по формуле (1.55)
| 
|
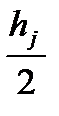
| 0-0,4 0,4-0,8 | 0,5 4,5 | 0,05 | 0,4 | |||
| 0,8-1,2 1,2-1,6 | 0,10 | 1,0 | ||||
| 12,5 | 12,5 | 0,225 | 1,4 | |||
| 1,6-2,0 2,0-2,4 2,4-2,8 2,8-3,2 3,2-3,6 3,6-4,0 | 0,295 | 1,8 | ||||
| 16,5 | 16,5 | 0,46 | 2,2 | |||
| 0,63 | 2,6 | |||||
| 12,0 | 12,0 | 0,75 | 3,0 | |||
| 6,5 | 6,5 | 0,815 | 3,4 | |||
| 12,0 | 12,0 | 0,935 | 3,8 | |||
| 4,0-4,4 4,4-4,8 4,8-5,2 5,2-5,6 | 0,995 | 4,8 | ||||
| Проверка | 99,5 | 99,5 |
Эмпирическая функция распределения 
, для каждого j-го интервала определяется по формуле 
; (j =1,2,3… H)
где п — объем выборки; Н — количество объединенных интервалов; 
- количество точек в 1-м, во 2-м и j -м интервалах.
Пример подготовки исходных данных для нанесения на вероятностные сетки при большом объеме выборки (п = 100) показан в табл. 1.4.
После подготовки исходных данных и определения эмпирических функций 
для малых выборок и 
для больших выборок работа проводится в следующей последовательности:
— на оси абсцисс наносят точки 
случайных величин (из вариационного ряда) с учетом коэффициентов масштаба в зависимости от предполагаемого закона распределения для небольших выборок (п < 50);
— для больших выборок (n > 50) на оси абсцисс наносят середины объединенных интервалов h j/2 с учетом коэффициентов масштаба для различных законов распределения;
— по оси ординат наносят точки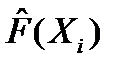 
для выборок с п < 50 или 
(для больших выборок), соответствующие нанесенным на оси абсцисс точкам Xi или hj/2;
— через нанесенные на вероятностную сетку точки (см. рис. 1.18) с координатами 
или 
проводят прямую так, чтобы нанесенные точки отклонялись от прямой как можно меньше.
Аппроксимирующая прямая проводится визуально (на глаз). При выборе той или иной вероятностной сетки следует предварительно оценить по имеющемуся вариационному ряду, какой закон можно принять для полученных статистических данных. Затем выбирается соответствующая вероятностная сетка, на нее наносятся эмпирические точки, через которые проводится аппроксимирующая прямая.
Если предварительную оценку предполагаемого закона распределения установить невозможно, то имеющиеся статистические данные следует заносить последовательно на экспоненциальную, нормальную, логарифмически-нормальную и Вейбулла вероятностные сетки. Если полученные статистические данные не подходят ни к одному из указанных законов (опытные точки не располагаются вблизи прямой), то следует использовать другой метод определения закона распределения (например, расчетный с построением гистограммы).
Проверка согласия эмпирического распределения с теоретическим производится по критерию А. Н. Колмогорова и для всех законов распределения одинакова. Сущность этой проверки заключается в следующем (см. рис. 1.18). Из всех точек, нанесенных на вероятностную сетку, выбирают такую, которая находится на наибольшем 
удалении (по оси ординат) от аппроксимирующей прямой,
Критерий согласия А. Н. Колмогорова определяется по формуле
, (1.56)
где 
- критерий согласия;
п - объем выборки;
- определяется в долях 
(см. рис. 1.18).
Учитывая неравномерность ординатных шкал и их масштаб, следует ожидать наибольшие ошибки для различных законов в диапазонах, приведенных в табл. 1.5. Если при проверке согласия не удовлетворяется условие (1.56), то эмпирический закон распределения не подходит к данной выборке.
| Таблица 1. 5
Диапазоны шкал, в которых возможны максимальные отклонения
| |
| Закон распределения | Диапазон шкалы |
| Нормальный и логарифмически-нормальный | 0,10 – 0,90 |
| Экспоненциальный | 0 – 0,50 |
| Вейбулла | 0,30 – 0,99 |
В этом случае следует использовать вероятностную сетку для другого закона и снова проверить согласие эмпирического и теоретического распределения. Если ни один из четырех указанных выше законов распределения не подходит к данной выборке, то следует применить другой способ определения закона распределения.
На основе графического изображения различных законов распределения при помощи вероятностных сеток можно определить точечные оценки параметров этих законов. Известно, что каждый закон характеризуется своими параметрами (табл. 1.6).
| Таблица 1.6 Основные законы распределения и их параметры | ||
| Закон распределения | Функция распределения | Параметры закона |
| Нормальный | 
| a;s |
| Логарифмически-нормальный | 
| 
|
| Экспоненциальный | 1- 
| l |
| Вейбулла | 1- 
| l;b |
Определить оценки параметров распределения — это определить их численные значения.
Для каждого закона распределения существует своя методика определения параметров.
а). Нормальный закон. Параметр 
определяется следующим образом. Из точки А (см. рис. 1.19), находящейся на пересечении аппроксимирующей прямой и линии, проведенной из точки = 0,5 параллельно оси абсцисс, необходимо провести прямую параллельно оси ординат до пересечения с осью абсцисс. Точка , лежащая на оси абсцисс, и будет искомой величиной параметра .
Параметр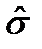 
определяется в виде отрезка (см. рис. 1.19), заключенного между вертикальными линиями, проведенными из точки А и точки на аппроксимирующей прямой, соответствующей =0,16 (или 0,84). Параметры и 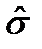являются размерными величинами и измеряются в единицах случайной величиных. При определении численных значений и 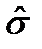следует учитывать коэффициент масштаба оси абсцисс.
б). Логарифмически-норм.альный закон. Для этого закона шкала ординат 
и шкала для нормального закона одинаковы. Поэтому методика определения параметров 
и 
для логарифмически-нормального закона остается такой же, как и для нормального закона.
Однако следует учитывать, что 
и 
где х — численные значения случайной величины.
в). Экспоненциальный закон. Это закон однопараметрический. Его параметр l определяется по формуле 
,
где Kx - коэффициент масштаба оси абсцисс;
tga - тангенс угла наклона эмпирической прямой к оси абсцисс (см. рис. 1.18).
Параметр l является размерной величиной и измеряется в единицах обратной величины х.
г). Закон Вейбулла. Это закон двухпараметрнческий, определяемый параметрами l и b. Схема определения этих параметров показана на рис. 1.20. Эмпирическая прямая 
, проведенная на вероятностной сетке распределения Вейбулла, отсекает на оси абсцисс отрезок ОА. На основе этого отрезка определяется параметр 
из уравнения OA= 
или 
, где 
- коэффициент масштаба оси абсцисс.
Параметр 
определяется по формуле 
, где tg a - тангенс угла наклона эмпирической прямой к оси абсцисс.
Здесь параметр - безразмерная величина, а параметр 
имеет размерность, обратную размерности случайной величины х.
После определения точечных оценок параметров законов распределения производятся точечная и интервальная оценки показателей надежности.
Показатели надежности, определяемые на основе статистических (опытных) данных, всегда являются приближенными значениями истинных теоретических значений этих показателей, характеризующих всю генеральную совокупность изделий. По р