Рассмотрим задачу нелинейного программирования:
f(x1,x2,…,xn) → max (19)
gi(x1,x2,…,xn) ≤ bi, (20)
xj ≥ 0 (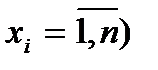 , (21)
, (21)
где f и gi - некоторые функции п переменных x1,x2,…,xn.
Определение 2 Задача (19)-(21) называется задачей выпуклого nрограммирования, если функция f (x1,x2,…,xn ), является вогнутой (выпуклой), а функции gi (Х) (i= 1, т) выпуклыми.
Определение 3. Множество допустимых решений задачи (19) - (21 удовлетворяет условию регулярности по Слейтеру, если существует, по крайней мере, одна точка Xi, принадлежащая области допустимых решений такая, что gi (Xi) < bi; (i = 1 ,т).
Теорема 1. Любой локальный максимум (минимум) задачи выпуклого nрограммирования является глобальным максимумом (минимумом).
Классический метод множителей Лагранжа не применим, если ограничения в задаче нелинейного программирования представляют собой неравенства.
Одним из путей решения такой задачи является использование теоремы Куна –Таккера. Эта теорема занимает центральное место в теории нелинейного программирования.
Необходимы и достаточные условия существования экстремума нелинейной функции в заданных ограничениях Куна –Таккера выведены также из предложения Лагранжа о переносе ограничений в целевую функцию. Таким образом, Кун и Таккер обобщили метод множителей Лагранжа на случай, когда система ограничений задачи нелинейного программирования включает как равенства, так и неравенства.
Имеются сведения о том, что задачу определения необходимых условий существования экстремума таких функций независимо от Гарольда Куна и Альберта Таккера решил в своей дипломной работе и Вильям Каруш.
Теорема 2 (теорема Куна-Таккера).
Для того, чтобы вектор Х* = (х*1,х*2, …,х*n), был решением задачи выпуклого программирования (19-21) (точка Х* была бы точкой глобального минимума функции) необходимо и достаточно, чтобы существовал такой вектор Λ* = (λ*1, λ*2, …, λ*m), при котором имеют место неравенства
Х* ≥ 0 и Λ* ≥ 0, (25)
L(X*, Λ) ≤ L(X*, Λ*) ≤ L(X, Λ*) (26)
для всех xi ≥ 0 и λi ≥ 0.
Данную теорему иногда называют теоремой о седловой точке, поскольку левое из неравенств (26) означает, что функция Лагранжа L(X, Λ)достигает минимума при Х = Х*, как функция переменного Х, независимо от значений Λ при λi ≥ 0 (i = 1,2,…,m), а правое из неравенств (26) означает, что функция Лагранжа L(X, Λ)достигает максимума при Λ = Λ* как функция переменного Λ, независимо от значений Х при xi ≥ 0, i = 1,2,…, n.
Если предположить, что функция Лагранжа L(X, 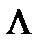 ) непрерывно дифференцируема по всем х и по всем λ, то теорему Куна-Таккера можно формально записать системой неравенств (условиями Каруша- Куна- Таккера), определяющей необходимые и достаточные условия существования седловой точкой функции Лагранжа (Х*,
) непрерывно дифференцируема по всем х и по всем λ, то теорему Куна-Таккера можно формально записать системой неравенств (условиями Каруша- Куна- Таккера), определяющей необходимые и достаточные условия существования седловой точкой функции Лагранжа (Х*, 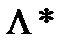 ), т. е. решения задачи выпуклого программирования. Эти выражения имеют следующий вид:
), т. е. решения задачи выпуклого программирования. Эти выражения имеют следующий вид:
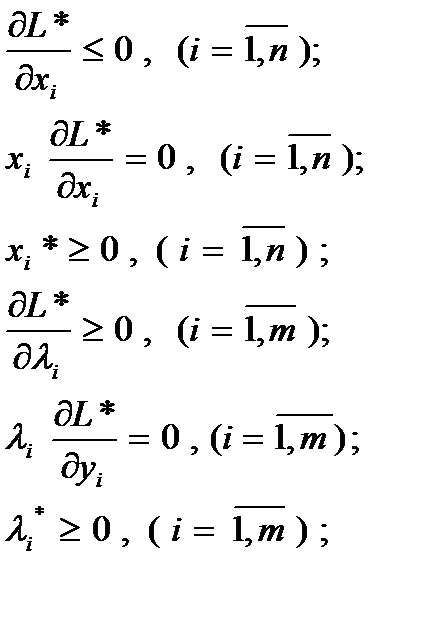
 (27)
(27)
где 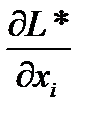 и
и  значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
Множество Х удовлетворяет условию регулярности по Слейтеру, если существует такая допустимая точка х 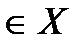 , что все g i(x) < 0, i = 1,2,…,m – неравенство строгое (если bi = 0) или, что тоже самое g i(x) < bi, i = 1,2,…,., если bi > 0.
, что все g i(x) < 0, i = 1,2,…,m – неравенство строгое (если bi = 0) или, что тоже самое g i(x) < bi, i = 1,2,…,., если bi > 0.
Важность условия регулярности по Слейтеру покажем на примере.
Пусть требуется решить задачу:
- целевая функция линейна (выпукла и вогнута одновременно)
F(x) = x → max;
- ограничения – нелинейная функция g(x) = х2 ≥ 0.
Графическое решение этой задачи показано на рис. 4.
| х |
| у |
| F(x)у |
Рисунок 4 – Пояснения к условию Слейтера
Решением этой задачи является единственная точка х* = 0, т.е. условие регулярности по Слейтеру не выполняется.
Докажем это заявление. Запишем функцию Лагранжа
L(x,λ) = x + λ (0 - x2). Тогда условия Куна-Таккера примут вид
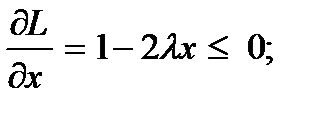
x 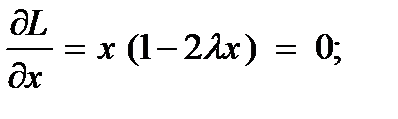
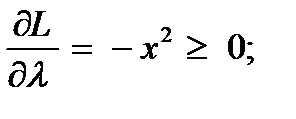
λ 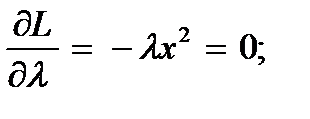
х ≥ 0; λ ≥ 0.
Очевидно, что эта система противоречива (решения не имеет).
Всем отмеченным требованиям, позволяющим записать необходимые и достаточные условия для седловой точки (Х*; 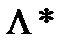 ) функции Лагранжа в виде выражений (30) - (35), удовлетворяет задача квадратичного программирования. Прежде чем сформулировать эту задачу, дадим некоторые определения.
) функции Лагранжа в виде выражений (30) - (35), удовлетворяет задача квадратичного программирования. Прежде чем сформулировать эту задачу, дадим некоторые определения.