При проведении анализа системы необходимо уметь оценить количественно основные свойства ее структуры. Практически любая структура системы может быть составлена из следующих шести типовых видов топологических структур (рис.9). Для конкретности положим, что структура состоит из пяти элементов.
| Кольцевая структура |
| Последовательная структура |
| Древовидная (иерархическая) структура |
| Радиальная (звездообразная) структура |
| Полносвязная структура |
Радиальная (звездообразная структура
Иерархическая (древовидная) структура
| Несвязная структура |
Полносвязная структура
Рисунок.9 – Виды топологических структур
Основными свойствами структур систем являются: связность, избыточность, компактность, степень централизации.
Связность структуры. Данная характеристика позволяет определить наличие обрывов в связях, висячие (несвязные) вершины и т.п.
Для неориентированных графов связность всех элементов в структуре соответствует выполнению условия:
 , (1)
, (1)
где aij – элемент матрицы смежности,
n – количество вершин графа.
Число 0,5 – следствие того, что при расчетах, одно и то же ребро графа, берется два раза.
Условие (1) можно записать в виде
 , (2)
, (2)
где m – число ребер в неориентированном графе.
Определим зависимость m = f(n) типовых структур (табл. 1.).
Таблица 1 – Связность типовых структур
| Типовая структура | m = f(n) |
| Последовательная | m = n - 1 |
| Кольцевая | m = n |
| Радиальная | m = n - 1 |
| Древовидная | Не имеет общего выражения |
| Полносвязная (каждый с каждым) | M = 0,5 n (n - 1) |
| Несвязная | Не имеет общего выражения |
Структурная избыточность. Это структурный параметр, отражающий превышение общего числа связей над минимально необходимым их числом. Избыточность принято обозначать R.
В общем виде избыточность структуры вычисляется по формуле
 . (3)
. (3)
Тогда, для типовых структур избыточность вычисляется по формулам, приведенным в табл. 2.
Таблица 2 – Избыточность типовых структур
| Типовая структура | m = f(n) |
| Последовательная | m = n – 1 → 
|
| Кольцевая | m = n → 
|
| Радиальная | m = n – 1 → 
|
| Древовидная | Не имеет общего выражения |
| Полносвязная (каждый с каждым) | m = 0,5 n (n - 1) → 
|
| Несвязная | Не имеет общего выражения |
Избыточность используется для косвенной оценки экономичности и надежности исследуемой структуры системы.
Для систем с большой избыточностью R > 0, с малой избыточностью R = 0, для несвязных структур R < 0. Очевидно, что чем больше R, тем потенциально более надежна система.
Для того, чтобы можно было учитывать неравномерность распределения связей и их несимметричность дополнительно к избыточности вводят характеристику неравномерности – среднеквадратическое отклонение степеней вершин от равномерного ε2 .
В общем виде ε2 выводится как функция от степени вершины ρ, числа вершин n и числа ребер m
 . (4)
. (4)
Показатель ε2 характеризует недоиспользованные возможности заданной структуры, имеющей m ребер и n вершин.
Для типовых структур ε2 вычисляется по формулам, приведенным в табл. 3.
Таблица 3 – Неравномерность типовых структур
| Типовая структура | m = f(n) |
| Последовательная | m = n – 1 → 
|
| Кольцевая | m = n → 
|
| Радиальная | m = n – 1 → 
|
| Древовидная | Не имеет общего выражения |
| Полносвязная (каждый с каждым) | m = 0,5 n (n - 1) → 
|
| Несвязная | Не имеет общего выражения |
Структурная компактность. Для ее оценки вводится параметр, отображающий близость элементов между собой. Близость 2-х элементов i и j определяется через минимальную длину пути для ориентированного графа (цепи для неориентированного) – dij. Тогда, сумма всех минимальных путей (цепей) между всеми элементами структуры, отражает общую структурную близость элементов анализируемой структуры.
Обозначим эту величину через Q и, в соответствии с определением, получим
 . (5)
. (5)
Для типовых структур близость Q вычисляется по формулам, приведенным в табл. 4.
Таблица 4 – Компактность типовых структур
| Типовая структура | m = f(n) |
| Последовательная | m = n – 1 → 
|
| Кольцевая | m = n 
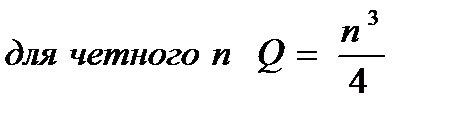
|
| Радиальная | m = n – 1 → 
|
| Древовидная | Не имеет общего выражения |
| Полносвязная (каждый с каждым) | m = 0,5 n (n - 1) → 
|
| Несвязная | Не имеет общего выражения |
Кроме этого показателя компактность структур оценивают с помощью:
- относительного показателя  , (6)
, (6)
где  - минимальное значение компактности для полносвязной структуры;
- минимальное значение компактности для полносвязной структуры;
- диаметром структуры  . (7)
. (7)
У полносвязного графа диаметр структуры равен единице и такая структура обладает максимальной избыточностью.
Результаты расчета структурных характеристик для типовых структур, изображенных на рисунке 9. сведены в табл. 5.
Таблица.5 – Сравнительная характеристика типовых структур из пяти элементов
| R | ε2 | Q | Q | d | |
| Последовательная | 1,2 | 1,0 | |||
| Кольцевая | 0,25 | 0,5 | |||
| Радиальная | 7,2 | 0,6 | 1,0 | ||
| Древовидная | 3,2 | 0,8 | |||
| Полносвязная | 2,5 | ||||
| Несвязная | -0,25 | - | - | - | - |
Расчеты для структур: последовательная, кольцевая, радиальная, полносвязная проведены по окончательным формулам, приведенным в таблицах 1 – 5. Расчет характеристик древовидной структуры выполнен непосредственно, исходя из данной конкретной структуры (рис.9):
- структурная избыточность
 ;
;
- среднеквадратическое отклонение

- структурная компактность  ;
;
 ;
;
 ;
;  ;
;
 ;
;  ;
;
Q = 6 + 9 + 5 + 8 +8 = 36;
- относительная структурная компактность

 ;
;
 = 5 4 = 20;
= 5 4 = 20;  =
=  ;
;
- диаметр  = max { 2, 3, 2, 3, 3} = 3.
= max { 2, 3, 2, 3, 3} = 3.
Из анализа результатов расчетов следуют выводы:
1) для несвязных структур структурная избыточность R < 0, для структур без избыточности (последовательная, радиальная, древовидная) R = 0, для структур с избыточностью по связям R > 0;
2) структуры без избыточности (последовательная, радиальная, древовидная) с R = 0 различаются по показателю ε2. Наибольшую неравномерность связей имеет радиальная структура;
3) наибольшую близость элементов (показатель Qотн) имеет структура типа полносвязный граф, наименьшую – последовательная.
Практическая часть
Задание 1. Задать структуру экономической системы посредством графа, матричным и множественным способами
Задание 2. Вычислить структурно–топологические характеристики структуры, изображенной на рисунке 1.10 (по вариантам) и по полученным результатам охарактеризовать заданную структуру.
Вопросы для самоконтроля:
1. Кто является основоположником теории графов?
2. В чем заключается существо задачи «о семи мостах»?
3. Изобразите обобщенную структуру замкнутой системы управления
4. Дайте определения понятиям: граф, цепь, путь, цикл, контур
5. Перечислите способы задания графов
6. Как составляется матрица смежности, матрица инцидентности?
7. Перечислите структурно-топологические характеристики системы
8. Что такое степень вершины (полустепень)?
9. Поясните понятие «связность графа»
10. Сформулируйте определение понятия «структура системы».
11. Перечислите и изобразите типовые структуры
Литература:
1. Методы оптимальных решений в экономике и финансах: учебнике/колл. авторов; под ред. В.М. Гончаренко, В.Ю. Попова.- М.:КНОРУС, 2013,-400с.
2. Оре О. Теория графов.- 2-е изд.-М.: Наука, Главная редакция физико-математической литературы, 1980, 336 с.
Отчет должен содержать:
1. Титульный лист
2. Ответы на контрольные вопросы (в письменной форме)
3. Выполнение заданий 1, 2
3. Выводы по результатам анализа структуры
* * *