Фирма производит два вида товаров А и В. Для производства х1 единиц товара А и х2 единиц товара В фирме требуется заранее приобрести
g(x1,x2) = x12 + x22 – x1x2
кг сырья. Из-за ограничений на объем склада количество сырья не может превышать 2100 кг.
Доход от реализации единицы товара А составляет 2000 усл. ед., от реализации единицы товара В – 1000 усл. ед.
Требуется обоснованно определить план выпуска товаров А и В, максимизирующий доход фирмы.
1. Составим экономико - математическую модель
Целевая функция: f(x1,x2) = 2000 x1 + 1000 x2 → max;
Функциональное ограничение: g(x1,x2) = x12 + x22 – x1x2 ≤ 2100;
Стандартные ограничения: х1, х2 ≥ 0.
Так как функция - ограничение нелинейная, имеем задачу нелинейного
программирования.
2. Проверим, не относится ли данная задача к задачам выпуклого программирования?
Целевая функция - линейная, следовательно и выпуклая и вогнутая.
Проверим функцию ограничение g(x1,x2) = x12 + x22 – x1x2 ≤ 2100.
В соответствии с критерием Сильвестра функция является выпуклой, если неотрицательны все главные миноры ее матрицы Гессе.
Вычислим первую частную производную по х1:
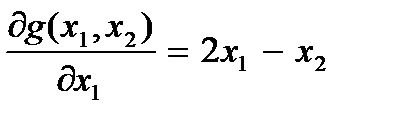 ;
;
Вычислим первую частную производную по х2:
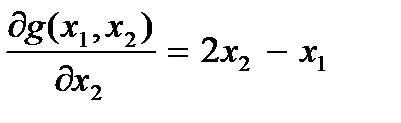 ;
;
Вычислим вторую частную производную по х1:
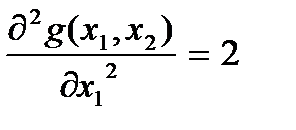 ;
;
Вычислим вторую частную производную по х2:
 ;
;
Так как функция - ограничение непрерывна, то ее вторые смешанные производные равны между собой, поэтому вычислим только одну из них
 . Тогда
. Тогда  .
.
Составим матрицу Гессе и проверим знаки угловых миноров
G = 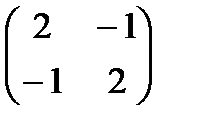 , Δ1 = 2 > 0; Δ2 =
, Δ1 = 2 > 0; Δ2 = 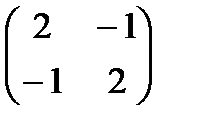 = 3 > 0, следовательно, функция, описывающая функциональное ограничение – выпуклая.
= 3 > 0, следовательно, функция, описывающая функциональное ограничение – выпуклая.
Таким образом, целевая функция выпуклая и вогнутая, функция – ограничение – выпуклая. Вывод: данная задача относится к классу задач нелинейного выпуклог о программирования.
Проверим выполнение условия регулярности Слейтера. Условие Слейтера выполняется, если существует такая допустимая точка Х0, в которой все нелинейные (функциональные) ограничения выполняются как строгие неравенства g (X0) < b).
Возьмем, например, допустимую точку Х0 = (1.1) (х1 > 0, x2 > 0).
В этой точке g(x1,x2) = x12 + x22 – x1x2 ≤ 2100;
g(1,12) = 12 + 12 – 1*1 < 2100, т.е. условие Слейтера выполняется.
Таким образом, для решения данной задачи можно воспользоваться методом множителей Лагранжа с применением теоремы Куна –Таккера (условие Куна -Таккера являются необходимым и достаточным условием существования в некоторой точке локального и глобального максимума).
3. Запишем функцию Лагранжа и условия Куна - Таккера в алгебраической форме.
Функция Лагранжа
L(x1,x2,λ) = 2000x1 + 1000x2 – λ(2100 – x12 – x22 +x1x2).
Условия Куна – Таккера (система уравнений и неравенств):
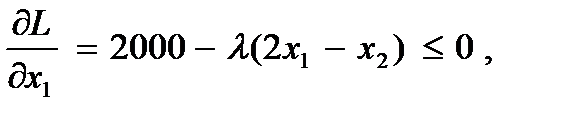 (28)
(28)
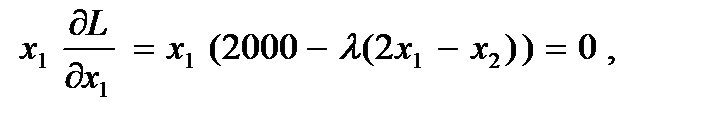 (29)
(29)
 (30)
(30)
 (40)
(40)
 (41)
(41)
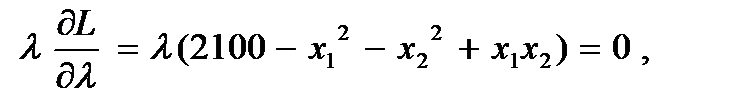 (42)
(42)
 . (43)
. (43)
Решим данную систему относительно х1,х2 и λ. Это задача не из самых простых, но она имеет однозначное решение. Покажем один из подходов к ее решению.
Из (28) и (43) следует, что λ ≠ 0. Из (28) и (43) следует также, что х1≠ 0.
Из (30) и (43) следует, что х2 тоже ≠ 0.
Из (29) 2000х1 – λх1 (2х1 – х2) = 0,

Из (40) 1000х2 – λх2 (2х2 – х1) = 0,
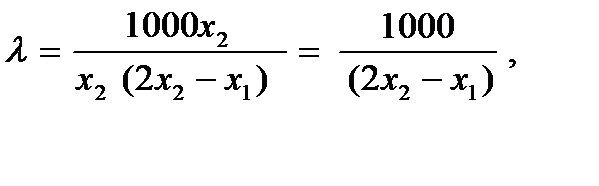
Так как равны левые части, то равны и правые части

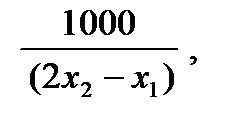 (разделим левую и правую части на 1000).
(разделим левую и правую части на 1000).


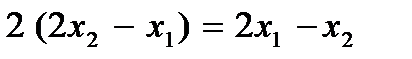 ,
,
 ,
,  →
→ 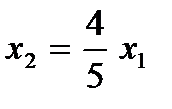 .
.
 .
.
Подставим в (42) 





х11 = 0 (не подходит по условию),

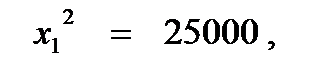
х12 = - 50 (не подходит по условию)
х1 = 50 ед,.
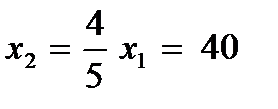 . ед.
. ед.
 .
.
При таком выпуске доход фирмы равен
f(50,40) = 2000 * 50 + 1000 * 40 = 140 000.
* * *