Среда, форма обучения - очная
Пара, Э31, Дисциплина Методы оптимальных решений, Лекция
Лекция 7
Тема лекции: Выработка и принятие оптимальных решений в задачах выпуклого программирования с ограничениями - неравенствами
Проблемы, подлежащие рассмотрению:
Выпуклые и вогнутые функции. Свойства выпуклых и вогнутых функций
Задача выпуклого программирования. Седловая точка функции Лагранжа. Теорема Куна – Таккера
Пример решения задачи выпуклого квадратичного программирования с ограничениями – равенствами
Выпуклые и вогнутые функции. Свойства выпуклых и вогнутых функций
Для задачи нелинейного программирования в общем случае не существует универсального метода решения, и эта задача является чрезвычайно сложной. Однако для ряда существенных для задачи ограничений она получает несложное решение. В частности в качестве такого ограничения выступает выпуклость задачи нелинейного ограничения.
Задача нелинейного программирования называется задачей выпуклого программирования при условии, что целевая функция f - вогнутая или выпуклая, а область допустимых решений, определяемая функциями ограничениями - выпуклая.
Множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки.
Если [a,b] - отрезок на числовой прямой и 
, то x = α a + (1 – α) b, где 0 ≤ α ≤ 1 или x = α1 a + α2 b, α1 + α2 = 1, α1 ≥ 0, α2 ≥ 0. (15)
Из этого утверждения следует и обратное: если выполняется (15), то .
Таким образом, отрезок [a,b] можно определить как множество всех точек х, удовлетворяющих условию (15).
Тогда, выпуклое множество – это множество, которое вместе с любой парой своих точек (a,b) содержит и все точки х, для которых выполняется (15).
|
|
Эти определения отрезка и выпуклого множества сохраняются для случая, когда a,b, …, x – точки n – мерного пространства (где операции в равенстве (15) выполняются покоординатно)).
Исходя из равенства (15), используя метод индукции, можно показать, что если М – выпуклое пространство, то 
для любых точек 
и любых действительных чисел ti ≥ 0, удовлетворяющих условию 
.
Определение 1. Функция F(X) = F(x1,x2,…,xn), определенная на выпуклом множестве М n – мерного пространства, называется выпуклой на этом множестве, если
(16)
для любых точек и любого числа 
Если у условии (16.) поменять знак ≤ на ≥, то получим определение вогнутой функции.
Если же в условии (16) вместо знака ≤ или ≥ записать знак строго неравенства, то получим определение строго выпуклой (строго вогнутой) функции.
На рис. 2 показан график функции одной переменной, строговыпуклой на всей числовой прямой.
Рисунок 2 – Графическое представление определения выпуклой функции
Из анализа графика, изображенного на рис. 2, следует, что для любой пары точек X1,X2 значений аргумента произвольную точку можно задать в виде Х = α Х1 + (1 – α) Х2 . Кроме того, неравенство (16) означает, что отрезок, соединяющий точки (Х1;F(X1)) и (X2;F(X2)) расположен не ниже графика функции на этом участке (для строго выпуклой функции этот отрезок расположен выше графика).
Пример 2. Установить выпуклость (вогнутость) функций, показанных на рис. 3.
Рисунок 3 – Графики типовых функций для проведения анализа
|
|
Результаты анализа:
- функции y = x2; y = ex являются всюду строго выпуклыми;
- функция y = ln x – строго вогнута на интервале (0, ∞);
- функция y = x (x – 3)2 не является, ни выпуклой, ни вогнутой на всей числовой оси, т.к. точка х = 2 разбивает ее на два участка: слева от этой точки – она строго вогнута, справа – строго выпукла.
Для выпуклых и вогнутых функций известно несколько очень важных свойств. При этом предполагается, что все рассматриваемые функции являются определенными на некотором выпуклом множестве М.
1. Если функция F(X) – выпукла, то функция (-F(X)) - вогнута.
2. Функция F(X) = C и линейная функция F(X) = aX + b являются всюду выпуклыми и всюду вогнутыми.
3. Если функции Fi(X), i = 1,2,…,m, выпуклы, то при любых действительных числах αi ≥ 0 функция 
также является выпуклой.
4. Если функция F(X) выпукла, то для любого числа α область решений неравенства F(X) < α является либо выпуклым множеством, либо пустым.
5. Если функции φi(X) – выпуклые при всех неотрицательных значениях переменных, то область решения системы неравенств φi(X) ≤ bi, i = 1,2,…,m является выпуклым множеством, если она не пуста.
6. Выпуклая (вогнутая) функция, определенная на выпуклом множестве М непрерывна в каждой внутренней точке этого множества.
7. Всякая дифференцируемая строго выпуклая (строго вогнутая) функция имеет не более одной стационарной точки (т.е. точки, в которой равны нулю все первые частные производные). При этом для выпуклой (вогнутой) функции стационарная точка всегда является точкой локального и глобального минимума (максимума).
8. Дважды дифференцируемая функция F(X) = F(x1,x2,…,xn) является выпуклой в том и только в том случае, если
|
|
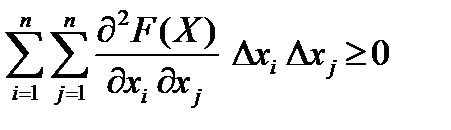(17)
для любых 
и ∆хi, ∆xj не обращающихся в нуль одновременно.
На практике для применения (17) используется критерий английского математика Дж. Сильвестра: условие (17) (функция является выпуклой) выполняется тогда и только тогда, когда неотрицательны все главные миноры ∆k матрицы вторых частных производных, т.е. определители
∆k =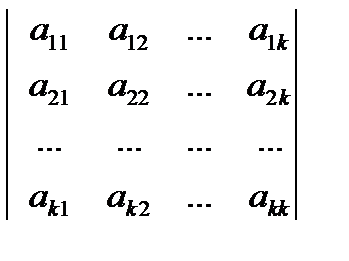 
, aij = 
, k = 1,2,…,n. (18)
Если все ∆k > 0, то неравенство (18) выполняется как строгое, и тогда функция F(X) является строго выпуклой.
Пример 4.1. Доказать, что функция F = 2x12 + x22 – x1x2 +5x1 – 6x2 + 8 является выпуклой
Решение.
1. Вычисляем первые частные производные
; 
;
2. Вычисляем вторые производные
; 
; 
; 
.
3. Составляем матрицу вторых частных производных
А = 
4. Составляем главные миноры матрицы А
∆1 = | 4 | > 0; ∆1 = | A | = 7 > 0.
Вывод: все главные миноры матрицы вторых частных производных больше нуля, следовательно, по свойству 8 заданная функция является выпуклой для всех Х.