Способ представления графов как показано на рис.3,4 называется графическим (геометрическим) изображением. Такой способ достаточно прост, нагляден, интуитивно понятен, но обладает существенным недостатком – сложностью введения графа в ЭВМ.
Пусть структура системы задана графом, изображенном на рис. 5.
Рисунок 5- Граф структуры системы
Матричное представление. Различают матрицы смежности, связности и инцидентности.
Матрица смежности  ,
,  , где n - число вершин графа.
, где n - число вершин графа.
Элементы матрицы неориентированного графа вычисляются по условию
 .
.
Для ориентированного графа
 .
.
Структура, изображенная на рис.5 может быть задана графом, показанным на рис.6.
| Номер вершины |
| Номер дуги |
Рисунок 6 – Граф структуры. изображенной на рис.5
Так для графа, изображенного на рис.6, матрица смежности имеет вид
А =  .
.
В матрице А – по строкам и по столбцам – номера вершин.
Матрица инцидентности 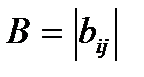 ,
,  , где n – число вершин графа, m – число ребер
, где n – число вершин графа, m – число ребер
Элементы матрицы неориентированного графа вычисляются по условию
 .
.
Для ориентированного графа
 .
.
Последнее определение поясняется рис.7.
| i |
| -1 |
| +1 |
Рисунок 7 – Пояснения к понятию инцидентности
Для графа, показанного на рис.6, матрица инцидентности примет вид
| Номера дуг |
| Вершины |

Множественное представление. Граф G(V) задается множеством вершин V и соответствием G, которое показывает, как связаны между собой вершины. Для каждой вершины i соответствие G определяет множество вершин G(i), в которое можно непосредственно попасть из вершины i. Это множество называется множеством правых инциденций.
Множество G-1(i) определяет все вершины, из которых можно непосредственно попасть в вершину i. Это множество называется множеством правых инциденций.
Таким образом, ориентированный граф задается перечислением (списком) множеств вида G(i) или G-1(i) для всех вершин графа.
Такой способ является наиболее компактным при задании исходной информации при исследовании (анализе и синтезе) структур системы особенно для иерархических структур, наиболее характерных для экономических систем.
Граф, изображенный на рис.6 посредством множественного представления, будет задан следующим образом: G(1) = (2,3); G(2) = (4); G(3) = (4,5); G(4) = (5); G(5) = (1) или G-1(1) = (5); G-1(2) = (1); G-1(3) = (1); G-1(4) = (2,3); G-1(5) = (3,4).
Цепью называется такая последовательность ребер Е0,Е1,…,Еk-1,Ek, когда каждое ребро Еk-1 соприкасается одним из своих концов с ребром Ek. Цепь можно задать и последовательностью вершин, которые она содержит.
Так, на графе, изображенном на рис.6, можно выделить цепь (1,2,4,5) или (1,2,3,5). Как правили, понятие цепь используют для описания неориентированных графов.
Путем называется такая последовательность дуг, когда конец каждой предыдущей дуги совпадает с началом последующей. На графе, изображенном на рис.6, имеется несколько путей (1,2),(2,4),(4,5) или (1,3),(3,4),(4,5). Понятие пути, как правило, используется для описания ориентированных графов.
Циклом называется такая конечная цепь, которая начинается и заканчивается в одной и той же вершине. Так в графе, изображенном на рис.6, можно выделить цикл (1,3,5,1). Понятие цикл используется, как правило, для неориентированных графов.
Контуром называется такой конечный путь, у которого начальная вершина первой дуги совпадает с конечной вершиной последней. Например, для графа, изображенного на рис.6, можно выделить контур (1,3), (3,5),(5,1).
Длина цепи (пути) – число ребер (дуг), входящих в цепь (путь) графа. Матрица смежности вершин графа А является матрицей непосредственных путей графа, имеющих длину, равную единице. Общее число транзитных путей L(k) длиной k может быть получено путем возведения матрицы А в степень k, т.е. L(k) = А k = Ak-1 A.
Любой элемент матрицы L(k) , например, lij(k) определяет число путей длиной k от вершины i к вершине j.
Степень вершины. Число ребер, инцидентных вершине i неориентированного графа, называют степенью вершины и обозначают ρ(i). Для графа, изображенного на рис.6: ρ(1) = 3, ρ(2) = 2, ρ(3) = 3, ρ(4) = 3, ρ(5) = 3.
Число дуг ориентированного графа, которые имеют начальной вершину i, называют полустепенью исхода вершины i и обозначают ρ+(i).
Число дуг ориентированного графа, которые имеют конечной вершину j, называют полустепенью захода вершины j и обозначают ρ-(j).
Для графа, изображенного на рис.6:
ρ+ (1) = 2, ρ+ (2) = 1, ρ+ (3) = 2, ρ+ (4) = 1, ρ+ (5) = 1.
ρ- (1) = 1, ρ- (2) = 1, ρ- (3) = 1, ρ- (4) = 2, ρ- (5) = 2.
Связность графа. Для неориентированных графов вводится понятие слабой связности или просто связности. Граф G(V) называется слабо связным (связным), если для любых вершин графа i и j существует цепь из вершины i в вершину j.
Для ориентированных графов вводится дополнительное понятие сильной связности. Граф G(V) называется сильно связным, если для любых вершин графа i и j существует путь из вершины i в вершину j.
На рис..8 показан несвязный граф, распадающийся на два сильно связанных подграфа.
Рисунок 8 – Несвязный граф, распадающийся на два сильно связных графа