Коэффициент соотношения заемных и собственных средств

Нормальное ограничение K_з.с. ≤ 1 показывает, какая часть деятельности предприятия финансируется за счет заемных средств.

Коэффициент маневренности рассчитывается как отношение собственных оборотных средств к обшей величине капитала:

Нормальное ограничение: K_м > 0,5. Коэффициент показывает, какая часть собственных средств вложена в наиболее мобильные активы. Чем выше доля этих средств, тем больше у предприятия возможность для маневренности в динамике; означает, что финансовое состояние хозяйствующего субъекта стабильно.

Комплексный анализ системы показателей финансовой статистики предприятий позволяет хозяйствующим субъектам всесторонне характеризовать состояние и потребность в денежных средствах, а также прогнозировать финансовую стратегию в условиях рыночной экономики.

Контрольные вопросы

Какими основными абсолютными показателями характеризуется финансовый эффект хозяйственной деятельности предприятия?
Каковы особенности методологии исчисления показателей рентабельности и их значимость в усговиях рыночной экономики?
Что понимают под финансовой устойчивостью хозяйствующего субъекта?
Какими показателями характеризуется платежеспособность предприятия?
Какими показателями характеризуются изменения финансовой устойчивости хозяйствующего субъекта?

27.1. Определение наращенной суммы на основе простых, сложных и смешанных процентов

27.1.1. Простые проценты

Под процентными деньгами или просто процентами (interest), понимают абсолютную величину дохода от предоставления денег в долг в любой форме: выдача ссуды, продажа товара в кредит, помещение денег на депозитный счет, учет векселя, покупка сберегательного сертификата или облигации и т.д.

При заключении финансового или кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки - отношение дохода (процентных денег) к сумме долга за единицу времени; измеряется в процентах или в виде десятичной или натуральной дроби.

Временной интервал, за который начисляют проценты называется периодом начисления. Проценты могут выплачиваться по мере их начисления (простые проценты) или присоединяться к основной сумме долга (сложные проценты).

Процесс увеличения суммы денег в связи с присоединением процентов называют наращением или ростом этой суммы, а саму сумму наращенной.

Процентные ставки могут быть фиксированными, дискретно изменяющимися и непрерывными.

27.1. Определение наращенной суммы на основе простых, сложных и смешанных процентов

27.1.1. Простые проценты

Процентные ставки могут быть фиксированными, дискретно изменяющимися и непрерывными.

27.1. Определение наращенной суммы на основе простых, сложных и смешанных процентов

27.1.1. Простые проценты

Процентные ставки могут быть фиксированными, дискретно изменяющимися и непрерывными.

27.1.2. Наращение по простой процентной ставке

Простые процентные вычисления применяются в финансовых обязательствах, как правило, на срок не больше года. При

простых процентах расчеты производятся исходя из постоянной базы, в качестве которой выступает первоначальная сумма долга. Под наращенной суммой понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока,

Наращенном сумма определяется умножением начальной суммы на множитель нарашения.

Для записи формулы наращения простых процентов примем обозначения:

Срок ссуды обычно измеряется в годах, соответственно i - годовая ставка. Каждый год приносит проценты в сумме PL Начисленные за весь срок проценты составят I=Pni

Тогда наращенная сумма (формула простых процентов):

S = P + I = P = Pni = P(1 + ni),

При сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору.

Величину п - общий срок ссуды выразим в виде дроби:

При расчете простых процентов предполагают, что к = 360 (12 месяцев по 30 дней) - это обыкновенные, или коммерческие проценты, или к - 365, 366 дней - точные проценты.

27.1.3 Сложные проценты

В средне - и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для нарашения, как правило, применяются сложные проценты. В соответствии с этим процесс роста первоначальной суммы происходит с ускорением. Ускорение вызвано гем, что на каждом этапе во времени (раз или несколько раз в год - каждый квартал, месяц и т.д.) начисленные проценты присоединяются к сумме, которая служила базой для их определения. Такой процесс называют капитализацией процентов.

Наращение по сложным процентам можно рассматривать как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления.

27.1.4. Наращение по сложным процентным ставкам

Пусть проценты капитализируются один раз в год (годовые проценты) на протяжении п лет,

Очевидно что в конце первого года проценты равны величине Р • i, а наращенная сумма составит: P + P * i = P(1 + i)

К концу второго года она достигнет величины:

P(1 + i) + P(1 + i) * i = P(1 + i) и т. д.

В конце n -го года наращенная сумма по сложным процентам:

S = P(1 + i)²

Проценты за зтот период равны I = S * P = P(1 + i)ⁿ и увеличиваются с каждым годом.

Величину (1 + i)ⁿ называют множителем наращения сложных процентов.

Значения этого множителя для целых чисел п приводятся в таблицах сложных процентов для п, равных от 1 до 50, 60, 70, 80. 90, 100 лет.

Если п > 50 и является целым числом, то искомую величину находят как произведение табличных значений для n₁ и n₂ (n = n₁ + n₂).

27.1.5.Определение наращенной суммы по смешанным процентным ставкам

Наращение по смешанным процентным ставкам применяется для случаев, когда п не является целым числом:

Сопоставление формул наращения по простым и сложным процентам позволяет сделать вывод:

27. 1.6. Эквивалентные ставки

Записав равенство, найдем ставку простых процентов, эквивалентную ставке сложных процентов:

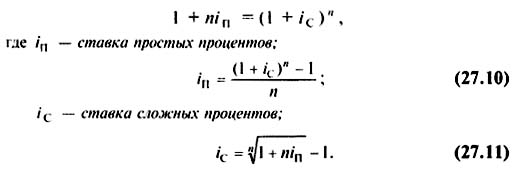
Эквивалентные ставки существенно зависят от срока начисления п.

27.1.7. Номинальная ставка

В современных условиях проценты капитализируются обычно не один, а несколько, т раз в году: по полугодиям, кварталам

и т.д. Некоторые зарубежные коммерческие банки практикуют ежедневное начисление процентов.

В таком случае годовая ставка называется номинальной ставкой процентов и обозначается через j. Тогда при m раз начислении процентов в году ставка, действительно начисляемая в каждом периоде, будет равна: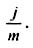

Формула наращения сложных процентов (при т раз начислении в году)

Увеличение m приводит к более быстрому процессу наращения, так как чаще происходит капитализация процентов. При большом числе периодов наращенная сумма может достичь астрономической величины, поэтому нельзя допускать возможность помещать капитал на очень большой срок.

27.1.8. Эффективная ставка

Эффективная ставка показывает, какая годовая ставка дает тот же процент, что и т - разовое наращение в год по ставке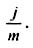

Обозначим эффективную ставку через i, поскольку она является годовой.

Множители наращения по определению должны быть равны:

Следовательно, эффективная ставка:

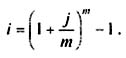
Как видим, эффективная ставка при т > 1 больше номинальной, при т = 1 равна ей: i = j

Замена в договоре номинальной ставки j при m -разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств участвующих сторон, так как обе ставки эквивалентны в финансовом отношении.

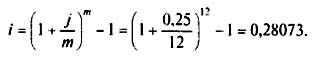
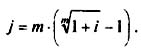
27.2. Математическое дисконтирование и банковский учет

В финансово-кредитных расчетах важную роль играет фактор времени. Это объясняется принципом "неравноценности" денег на разные временные даты. В связи с этим нельзя суммировать деньги на разные моменты времени.

Для сопоставимости денег, относящихся к разным датам, прибегают к дисконтированию, т. е. приведению к заданному моменту времени. Дисконтирование осуществляется при покупке банком или другим финансовым учреждением краткосрочных финансовых обязательств (векселей, тратт), оплата которых производится в будущем.

Следовательно, ставится задача, обратная определению наращения процентов: по заданной сумме 5, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды Р. В этих случаях говорят, что сумма S дисконтируется или учитывается. Сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты (разность S - Р = Д; - дисконтом (discont).

Величину P найденную с помощью дисконтирования, называют современной, капитализированной (приведенной) величиной суммы S,

В зависимости от вида процентной ставки применяют два метода дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.

27.2.1. Математическое дисконтирование

При математическом дисконтировании современная капитализированная величина суммы S определяется из уравнения (27.1):

Разность S - Р можно рассматривать не только как проценты, начисленные на P но и как дисконт с суммы 5, т. е. Д = S - Р.

Заметим, что по соглашению сторон дисконт может быть установлен и в виде абсолютной величины для всего срока (без расчета по формуле).

27.2.2. Банковский учет (учет векселей)

Суть операции учета векселя заключается в том, что банк или другое финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т. е. покупает (учитывает) его с дисконтом (т. е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. Владелец векселя с помощью его учета имеет возможность получить деньги, хотя не в полном объеме, однако раньше указанного срока.

При этом применяется учетная ставка d.

Размер дисконта, или сумма учета, удерживаемая банком, равен Snd.

Таким образом, сумма, выплачиваемая при учете векселя, будет равна:

Коэффициент соотношения заемных и собственных средств

Поиск по сайту