ДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА
С ПОДЧИНЕННЫМ ТОКОВЫМ КОНТУРОМ
Целью работы являются:
1. Изучение принципов построения и практической реализации систем подчиненного регулирования.
2. Овладение навыками расчета и настройки регуляторов системы подчиненного регулирования.
3. Расчет и практическое определение статических и динамических характеристик системы регулирования скорости при различных видах настройки регуляторов.
4. Сравнение полученных результатов и их сопоставление с аналогичными результатами исследования одноконтурной системы регулирования скорости (работа № 1).
Общие указания
Построение систем по принципу подчиненного регулирования представляет собой один из способов реализации систем автоматического управления с высокими статическими и динамическими характеристиками. Системы, построенные по многоконтурному варианту – принципу подчиненного регулирования, обладают существенными достоинствами. Идеи построения систем по принципу подчиненного регулирования возникли и успешно применяются при автоматизации электроприводов главным образом постоянного тока. Однако эти идеи с успехом могут быть использованы для решения задач синтеза и других систем управления. Сущность данного подхода заключается в том, что в системе помимо основной регулируемой величины рассматриваются и другие (промежуточные) координаты, определяющие состояние системы, а затем образуются контуры регулирования всех выделенных величин. Таким образом, получают многоконтурную систему, в которой контуры как бы вложены последовательно от внутреннего контура к внешнему – контуру регулирования основной физической величины. При таком подходе используется как бы метод последовательной коррекции в сочетании с корректирующими обратными связями. Каждый контур, начиная с внутреннего, настраивается таким образом, чтобы разомкнутый контур представлял собой реальную однократно интегрирующую систему. Реальность состоит в том, что реализовать идеальную интегрирующую систему не представляется возможным, поскольку в каждом контуре помимо больших постоянных времени объекта, подлежащих компенсации, содержатся одна или несколько малых, не компенсируемых постоянных времени (усилителей, преобразователей, фильтров).
 |
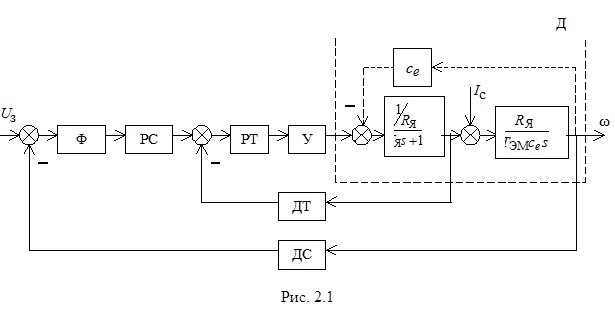Настройка регулятора обеспечивает реализацию контура как системы второго порядка с одним интегрирующим и одним инерционным звеньями, постоянная времени которого есть некомпенсируемая малая постоянная или сумма всех малых постоянных данного контура. Малая постоянная времени замкнутого внутреннего контура обычно является некомпенсируемой малой постоянной времени последующего внешнего контура, а если в этом контуре есть еще и свои малые постоянные времени (например, фильтров), то его малая постоянная времени снова образуется как сумма всех малых постоянных. В лабораторной работе рассматривается система регулирования скорости двигателя постоянного тока независимого возбуждения с подчиненным токовым контуром, структурная схема которой представлена на рис. 2.1. Данная структура включает следующие элементы: Ф - фильтр, предназначенный для сглаживания коллекторных пульсаций тахогенератора; РС - регулятор скорости; РТ - регулятор тока; У - усилитель мощности; Д - двигатель постоянного тока (пунктиром показана внутренняя обратная связь по ЭДС); ДТ - датчик тока; ДС - датчик скорости.
 |
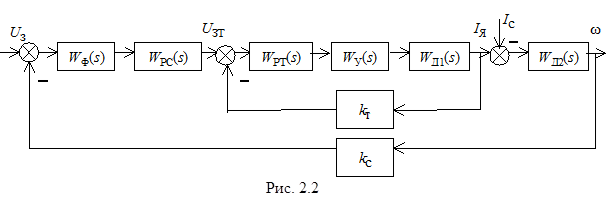В результате структурных преобразований избавляемся от перекрещивающихся связей и получаем структуру, представленную на рис. 2.2, включающую все ранее перечисленные элементы с указанием передаточных функций:
; 
?, 
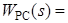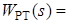? - требуется определить в результате расчета; 
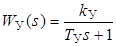; k т - коэффициент передачи обратной связи по току; k с - коэффициент передачи обратной связи по скорости.
Передаточная функция двигателя в результате преобразований представлена в виде двух звеньев W Д1(s)в контуре тока и W Д2(s)в контуре скорости: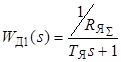 
для случая, неучитывающего влияния внутренней обратной связи по ЭДС, т. е. при T ЭМ >>T Я, или 
с учетом влияния обратной связи по ЭДС; 
, 
, 
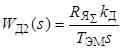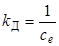, R Ш- сопротивление обратной связи по току.
Расчет контура тока
Расчет начинается с внутреннего контура - контура тока. В этом контуре в качестве компенсируемой части объекта принимается входящая в него передаточная функция двигателя W Д1(s). Некомпенсируемым звеном является усилитель, постоянную времени которого принимаем за малую постоянную времени контура тока, т. е. T μт = T У, где Т μт – малая некомпенсируемая постоянная времени контура тока. Тогда, в соответствии с изложенным, ставиться задача определения передаточной функции регулятора тока W PT(s) из условия получения передаточной функции разомкнутого контура тока W KT(s) в виде однократно интегрирующей системы, т. е.
,
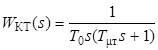где Т 0 – параметр, определяемый настройкой регулятора.
Известно, что динамические качества контура определяются видом передаточной функции замкнутого контура. Для замкнутого контура тока имеем
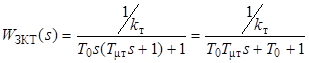. (2.1)
Выражение (2.1) может быть представлено как передаточная функция стандартного колебательного звена, т. е.
,
, 
,
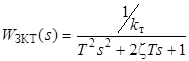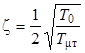где Т - постоянная времени колебательного звена; ζ - коэффициент затухания (или демпфирования) колебательного звена.
При ζ = 1, т. е. при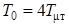 
имеем предельный случай апериодического звена. Однако при выборе соотношения 
, 
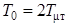обеспечивается большее быстродействие, поскольку в технических системах длительность процесса определяется временем вхождения в зону установившегося значения с точностью 
%. В случае 
и ζ=0.707 имеем колебательный процесс, но с максимальным перерегулированием всего 4.3 %, вот почему в этом случае быстродействие будет выше, чем при 
. Настройка контура на соотношение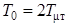 
и ζ = 0.707 является настройкой на модульный оптимум (МО). Итак, для контура тока имеем:
,
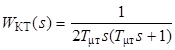а так как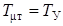 
,то
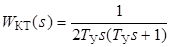. (2.2)
С другой стороны, из структурной схемы (рис. 2.2) имеем:
,
откуда
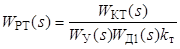. (2.3)
Подставив в (2.3) выражения передаточных функций всех звеньев, а W KT(s) из (2.2), получим передаточную функцию регулятора, при этом принято W Д1(s) без учета влияния ЭДС, так как в нашем случае Т ЭМ >>Т Я:
,
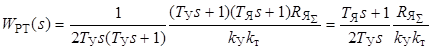или
,
где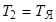 
; 
; 
.
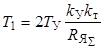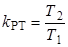Расчет контура скорости
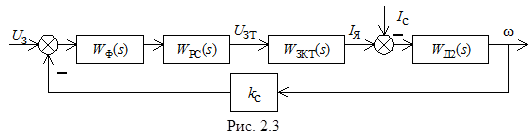
Контур скорости включает в себя замкнутый контур тока. Структурная схема представлена на рис. 2.3. При настройке контура на модульный оптимум передаточная функция контура имеет вид:
 |
,
где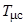 
- некомпенсируемая малая постоянная времени контура скорости.
Из структурной схемы рис. 2.3 имеем
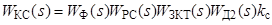. (2.4)
Из (2.4) выражаем передаточную функцию регулятора скорости:
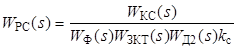, (2.5)
где 
.
Тогда, приняв за малую некомпенсируемую постоянную времени контура скорости Т μс величину, равную сумме малой постоянной времени контура тока 2 Т У и постоянной времени фильтра Т Ф, т. е.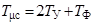 
, получим из (2.5) передаточную функцию регулятора скорости
. (2.6)
Таким образом, при настройке контура скорости на модульный оптимум получаем П-регулятор с коэффициентом передачи k РС, определяемым выражением (2.6).
Важнейшим показателем, характеризующим качество системы стабилизации скорости, является статическая точность ее работы, т. е. значение установившейся ошибки при возмущающем воздействии. Рассчитать установившиеся ошибки по управляющему и возмущающему воздействиям можно, используя передаточные функции системы по сигналу ошибки. Однако проще и нагляднее их можно выразить из уравнения равновесия прохождения сигналов в исследуемой структуре. Для нее можно записать (см. рис. 2.3):
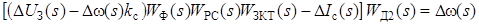. (2.7)
Уравнение (2.7) записано в приращениях по управляющему D U З(s) и возмущающему D I с(s) воздействиям. Выразить передаточные функции по соответствующему воздействию можно, полагая D I с(s) = 0 или D U з(s) = 0. Далее, устремив s ®0, получить значения установившихся ошибок. Положив D U з(s) = 0, выразим из (2.7) отношение Dω(s) / D I с(s) и после подстановки в него выражений для всех входящих передаточных функций и упрощений получим
, 
,
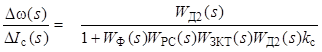и учитывая, что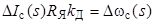 
, получим
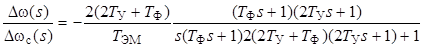. (2.8)
В установившемся режиме (s ®0) относительный перепад скорости Dω / Δωс определяется из (2.8) при s ®0 и выражается
,
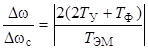где Δωс - естественный статический перепад скорости от приложенной нагрузки.
Если полученное таким образом значение ошибки не соответствует техническим требованиям, необходимо повысить порядок астатизма в той части системы, которая существует слева от места приложения возмущающего воздействия (см. рис. 2.3). Чаще всего в этом случае переходят к настройке контура скорости на симметричный оптимум (СО), т. е. используют в качестве регулятора скорости ПИ-регулятор. В нашем случае
.
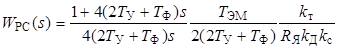При настройке контура скорости на симметричный оптимум в системе наблюдается значительное увеличение динамической ошибки (перерегулирования) по управляющему воздействию, обусловленное наличием в регуляторе скорости форсирующего звена с передаточной функцией W (s) = 1 + 4(2 T У +T Ф) s. Для того чтобы переходный процесс соответствовал прежней настройке контура на модульный оптимум, необходимо на входе системы перед задающим воздействием включить звено с передаточной функцией обратной передаточной функции форсирующего звена, то есть
 |
.
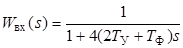Данное входное звено W вх(s) играет роль задатчика интенсивности. Структурная схема с входным звеном представлена на рис. 2.4.