ЭЛЕКТРОМЕХАНИЧЕСКАЯ СИСТЕМА СТАБИЛИЗАЦИИ

ПОЛОЖЕНИЯ МАГНИТНОГО ТЕЛА

Целью работы являются:

1. Изучение принципа действия и математического описания системы стабилизации положения магнитного тела.

2. Уточнение математической модели объекта управления и системы в целом.

3. Расчет параметров корректирующих устройств (в том числе машинными методами).

4. Экспериментальное определение статических и динамических характеристик системы регулирования.

Общие указания

На рис. 3.1 представлена структурная схема системы автоматического регулирования положения ферромагнитного тела (ФМТ), на которой приняты следующие обозначения: ОУ (объект управления) - ФМТ (полый шарик из Ni), подвешиваемое в поле электромагнита (ЭМ) под действием электромагнитной силы (F _ЭМ) на расстоянии d от ЭМ; ДОС (датчик обратной связи) - датчик положения, дающий информацию о положении ФМТ относительно ЭМ; УПТ - усилитель постоянного тока, питающий обмотку ЭМ (I _ЭМ). Напряжение U _ЭМ на выходе усилителя, подаваемое на обмотку ЭМ, изменяется в соответствии с сигналом рассогласования (D U). Процесс изменения тока в обмотке ЭМ имеет вид

, (3.1)

где r _ЭМ - сопротивление обмотки, Ом; w - число витков в обмотке; Ф - магнитный поток, Вб.

Умножая (3.1) на I _ЭМ dt, получаем: . (3.2)

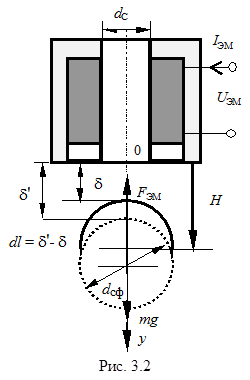Предположим, что в рассматриваемой системе происходит перемещение подвешиваемого ФМТ вдоль направления, противоположного направлению силы тяжести на dl (рис. 3.2). При этом магнитная энергия системы W изменяется на dW и совершается механическая работа F _ЭМ dl. Из закона сохранения энергии следует, что энергия, сообщаемая источником напряжения за время dt, должна равняться сумме энергии, выделяющейся в виде теплоты в сопротивлении обмотки ЭМ, энергии, затрачиваемой на совершение механической работы, и приращения энергии магнитного поля dW:

. (3.3)

Из сопоставления (3.2) и (3.3) следует:

.

Электромагнитная сила F _ЭМ может быть выражена через магнитную проводимость G воздушного зазора:

, (3.4)

, (3.5)

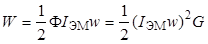. (3.6)

С учетом (3.4) – (3.6) выражение для электромагнитной силы имеет вид

. (3.7)

Знак "–" в (3.7) означает, что положительному электромагнитному усилию F _ЭМ соответствует уменьшение воздушного зазора d. Для вычисления F _ЭМ по (3.7) необходимо иметь выражение для расчета проводимости воздушного зазора между плоскостью и сферой для электромагнита броневого типа. Согласно [1], магнитную проводимость воздушного зазора под сердечником можно определить по формуле:

, (3.8)

где ; R _сф - радиус сферы, см; r _с - радиус сердечника, см.

Уравнение движения подвешиваемого ФМТ имеет вид:

, (3.9)

где m - масса ФМТ, кг; H - расстояние от ЭМ до центра тяжести ФМТ, см.

Вычисляемая согласно формул (3.7) и (3.8) электромагнитная сила F _ЭМ(d, I _ЭМ) представляет нелинейную зависимость, вследствие этого уравнение (3.9) оказывается нелинейным. Однако, учитывая малый диапазон регулирования, можно выделить участок, на котором с допустимой точностью можно принять линейную модель ОУ (ФМТ). Для этого, разлагая правую часть выражения (3.9) в ряд Тейлора и ограничиваясь только первыми членами ряда, получим линеаризованное уравнение движения подвешиваемого ФМТ в отклонениях:

Откуда получаем

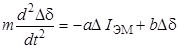, (3.10)

так как 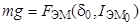и

где

где d₀ - зазор, соответствующий уравновешенному положению ферромагнитного тела; 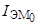- значение тока в обмотке ЭМ, соответствующее уравновешенному положению ФМТ.

Переходя в (3.10) к изображениям по Лапласу, получаем передаточную функцию:

. (3.11)

Знак "–" в (3.11) означает, что увеличению тока в обмотке ЭМ соответствует уменьшение воздушного зазора. В соответствии со структурной схемой (рис. 3.1) входной величиной ОУ (ФМТ) является электромагнитная сила (F _ЭМ), а ПФ ОУ определяется как . Однако при составлении математического описания движения подвешиваемого тела не удалось выделить F _ЭМ как координату и получить передаточную функцию ОУ в виде . Поэтому приведенный вывод математической модели ОУ (ФМТ) неразрывно связан с выводом математической модели электромагнита. Изложенное можно проиллюстрировать структурной схемой, приведенной на рис. 3.3. Обмотка ЭМ имеет передаточную функцию инерционного звена 1-го порядка:

, (3.12)

где ; .

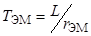Передаточную функцию (3.11), представляющую собой согласно рис. 3.3 последовательное соединение ЭМ и ОУ, лучше представить в стандартном виде

(3.13)

.

Согласно проведенным исследованиям, измерениям и расчетам исходные данные для определения числовых значений параметров передаточных функций (3.12) и (3.13) следующие: m = 0.0107 кг; R _сф = 0.016 м; [ = 1.5 А, d₀ = 2.2 cм]; [ = 1.6 А, d₀ = 2.4 cм]; [ = 1.7 А, d₀ = 2.6 cм]; [ = 1.8 А, d₀ = 2.8 cм]; [ = 1.9 А; d₀ = 2.95 cм]; r _с = 6 см; L = 0.185 Гн; r _ЭМ = 23 Ом. Расчет параметров a и b в (3.11) и (3.13) из-за сложности вычислений осуществлялся машинным способом. Результаты расчета приведены для точки равновесия [ = 1.7 А, d₀ = 2.6 cм]: a = 39.2; b = 12.7. Результаты расчетов параметров а и b для других точек равновесия не приводятся, так как их значения отличаются не более чем на 3 % от представленных значений параметров.

Для расчета системы регулирования положения ФМТ согласно рис. 3.1 необходимо определить вид передаточных функций УПТ и ДОС, а также значения их параметров. При проведении лабораторных занятий на этом же макете по курсу "Элементы и устройства систем управления" указанные элементы являются объектом исследования, в результате проведения которого необходимо получить статические и динамические характеристики УПТ и ДОС, используемые в дальнейшем при выполнении работ по данному курсу. Передаточные функции УПТ и ДОС имеют следующий вид:

, .

Таким образом, структурная схема системы регулирования, подлежащая исследованию и расчету, представлена на рис. 3.4. В представленной структурной схеме на входе и выходе каждого звена указаны отклонения соответствующих переменных от установившихся значений. Приращение регулируемой величины системы Dd обусловлено переходным процессом, вызванным изменениями задающего воздействия на величину D U _з. Коэффициент передачи датчика ДОС взят со знаком

"–", так как статическая характеристика ДОС, исходя из которой определялся k _ДОС, δ показывает, что уменьшение воздушного зазора ведет к увеличению выходного напряжения, снимаемого с ДОС.

Поскольку рассматриваемая система имеет в своем составе неминимально-фазовое звено, то согласно частотному критерию устойчивости Найквиста при K = k _У k _{обм. ЭМ} k _ОУ k _ДОС > 1 данная система будет неустойчива и для обеспечения ее работоспособности требуется применение корректирующих устройств. Детальный анализ данной системы регулирования показал, что для ее стабилизации единственно приемлемым решением является использование последовательных корректирующих устройств. Для реализации системы регулирования положения ФМТ необходимо рассчитать корректирующие цепи двух типов:

1) дифференцирующую пассивную RC-цепь (Д-RC-цепь);

2) интегро-дифференцирующую пассивную RC-цепь (ИД-RC-цепь), при заданном значении коэффициента передачи УПТ в соответствии с вариантом: 1) k _У = 50; 2) k _У = 60; 3) k _У = 80; 4) k _У = 90; 5) k _У = 100.

Структурная схема системы регулирования с последовательной коррекцией (ПК) представлена на рис. 3.5. Здесь же показано наличие возмущающего воздействия f, реализуемого в системе с помощью вентилятора, сдувающего при его включении ФМТ.