ПЛАТФОРМЫ("ВЕРТОЛЕТ")
Целью работы являются:
1. Изучение возможных принципов построения системы управления положением механического объекта.
2. Исследование одноконтурной системы регулирования углового положения платформы, расчет и реализация возможных вариантов корректирующих устройств.
3. Определение качественных показателей работы одноконтурной системы регулирования углового положения платформы для различных вариантов структурной организации.
4. Изучение принципов построения системы подчиненного (многоконтурного) регулирования положения платформы.
5. Ознакомление с принципами расчета регуляторов отдельных контуров системы подчиненного регулирования.
6. Аналитический расчет и экспериментальное определение статических и динамических характеристик системы подчиненного регулирования положения механического объекта.
Общие указания
Описание поворотной платформы как механического объекта управления подробно рассматривается в лабораторной работе № 4 [2]. Возможны различные способы реализации замкнутой системы регулирования углового положения платформы. В качестве одного из них предложена одноконтурная система управления, структурная схема которой изображена на рис. 4.1.
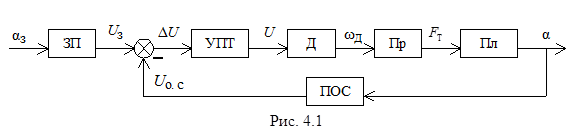
Рассмотрим элементы структурной схемы и их математическое описание. В соответствии с исследованием ОУ (поворотной платформы (Пл)), проведенном в работе № 4 [2], передаточная функция его линеаризованной модели представляется в виде колебательного звена
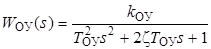 ,
,
где параметры k ОУ, Т ОУ и ζ меняются в зависимости от углового положения платформы и положения противовеса.
При расчете системы регулирования рекомендуется принять усредненные значения указанных параметров, полученные в ходе исследования ОУ.
В качестве исполнительного двигателя в данной работе используется типовой для данной лаборатории электродвигатель постоянного тока типа Д-25-Г. Передаточная функция двигателя имеет вид
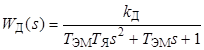 ,
,
где  рад/(В·с); Т ЭМ = 0.16 с; Т Я = 2.7·10–3 с.
рад/(В·с); Т ЭМ = 0.16 с; Т Я = 2.7·10–3 с.
В работе используется трехкаскадный усилитель постоянного тока, обеспечивающий линейность характеристики в пределах ±27 В при максимальном токе нагрузки I = 2 А, имеющий передаточную функцию
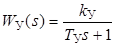 ,
,
где k У = 10…70; Т У = 1.4 · 10–3 с.
Пропеллер имеет сложную нелинейную характеристику, однако, как отмечалось в работе № 4 [2], в линеаризованном варианте передаточная функция пропеллера принимается в виде безынерционного звена
 ,
,
где коэффициент передачи пропеллера был определен путем аппроксимации его экспериментальных характеристик k п = 0.000765 Н · с/рад.
Потенциометрический датчик (ПОС) для измерения углового положения платформы зафиксирован на оси, вокруг которого вращается платформа, и имеет следующие характеристики: тип датчика - ПТП 5К1, сопротивление 10 кОм, рабочий диапазон α = 330°, напряжение питания датчика U п = 93 В.
Передаточная функция датчика
 ,
,
где 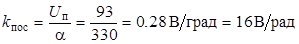 .
.
Результаты анализа поведения системы регулирования углового положения платформы (в том числе в ходе выполнения данной лабораторной работы) показывают, что система неустойчива уже при коэффициенте передачи усилителя k У = 15. Таким образом, возникает задача обеспечения устойчивости и хороших статических и динамических показателей качества системы регулирования, решение которой может быть достигнуто использованием различных средств. В данной лабораторной работе рассматриваются два варианта реализации системы регулирования углового положения платформы.
Вариант 1. Одноконтурная система регулирования с последовательной интегро-дифференцирующей RC-цепью (ПКЦ).
Достоинства и недостатки данного метода коррекции общеизвестны. Главным достоинством ПКЦ является простота расчета и реализации. Однако, учитывая нелинейный характер ОУ, представленного колебательным звеном, параметры которого принимаются усредненными и постоянными, а в реальности, как уже отмечалось, меняются, использование ПКЦ не обеспечивает высоких качественных показателей работы системы в статике и динамике во всем диапазоне регулирования положения платформы.
Обычно ПКЦ включается на вход усилителя. Задача лабораторной работы по данному варианту состоит в расчете параметров ПКЦ, экспериментальном определении статических и динамических показателей качества работы системы регулирования и сравнение их с расчетными.
Вариант 2. Трехконтурная система подчиненного регулирования углового положения поворотной платформы.
Основные принципы построения систем подчиненного регулирования изложены в лабораторной работе № 2 настоящего пособия, там же отмечены достоинства такой организации работы систем и даны идеи их расчета. В данной лабораторной работе исследуется трехконтурная система подчиненного регулирования, структурная схема которой представлена на рис. 4.2. На схеме используются следующие обозначения: УПТ - усилитель постоянного тока; Д1 - Д2 - Д3 - двигатель; Пр - пропеллер; Пл - платформа; ДТ - датчик тока; ДЭ - датчик ЭДС; ДП - датчик положения; РТ - регулятор тока; РЭ - регулятор ЭДС; РП - регулятор положения. 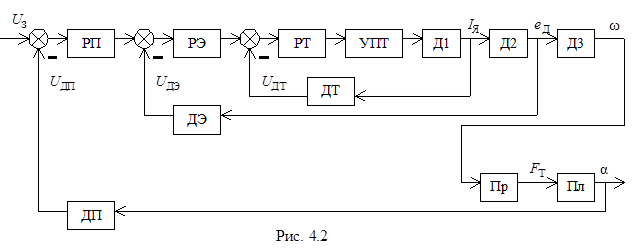
Двигатель, имеющий передаточную функцию W Д(s), в данном случае представлен в виде трех последовательно соединенных звеньев с передаточными функциями W Д1(s), W Д2(s) и W Д3(s), что необходимо для выделения промежуточных координат. На выходе передаточной функции W Д1(s) получим ток якоря, на выходе передаточной функции W Д2(s) имеем значение ЭДС двигателя и, наконец, на выходе W Д3(s) имеем значение скорости вращения вала двигателя.
Выбор в качестве промежуточной координаты значения ЭДС, а не скорости, объясняется конструкцией макета, в котором нет тахогенератора, установка которого повлекла бы кардинальные изменения конструкции.
Согласно общим указаниям к работе № 2 имеем
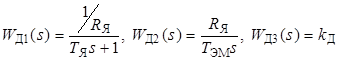 ,
,
где R Я = R ЯД + R Ш - полное сопротивление якорной цепи; R Ш = 1 Ом - добавочное сопротивление в якорной цепи для реализации обратной связи по току.
В соответствии с изложенным ранее принципом расчета контуров на модульный оптимум (см. также работу № 2) нетрудно последовательно, начиная с внутреннего контура, рассчитать регуляторы тока, ЭДС и положения.
Некомпенсируемой частью контура тока является усилитель, имеющий малую постоянную времени Т У. Таким образом, некомпенсируемая малая постоянная времени контура тока Т μ будет равна Т У, Т μ = Т У. Передаточная функция разомкнутого контура тока  . Тогда передаточная функция регулятора тока будет иметь вид
. Тогда передаточная функция регулятора тока будет иметь вид
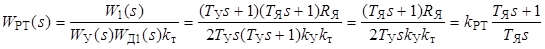 , (4.1)
, (4.1)
где 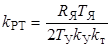 - коэффициент передачи регулятора тока.
- коэффициент передачи регулятора тока.
Выразим передаточную функцию замкнутого контура тока
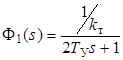 . (4.2)
. (4.2)
Учитывая передаточную функцию датчика ЭДС 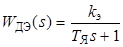 , где k э = 0.44, можно рассчитать регулятор ЭДС.
, где k э = 0.44, можно рассчитать регулятор ЭДС.
Для этого контура некомпенсируемой малой постоянной является сумма малых постоянных замкнутого контура тока 2 Т У и датчика ЭДС, равная якорной постоянной двигателя Т Я, т. е. 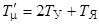 .
.
При настройке на модульный оптимум передаточная функция разомкнутого контура ЭДС
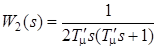 . (4.3)
. (4.3)
С другой стороны (см. рис. 4.2),
 . (4.4)
. (4.4)
Тогда, учитывая (4.2) и (4.3), выразим из (4.4) передаточную функцию регулятора ЭДС:


Учитывая, что 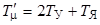 , передаточная функция регулятора ЭДС будет иметь вид
, передаточная функция регулятора ЭДС будет иметь вид
 , (4.5)
, (4.5)
где 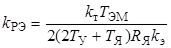 - коэффициент передачи регулятора ЭДС.
- коэффициент передачи регулятора ЭДС.
Передаточная функция замкнутого контура ЭДС  .
.
Таким образом, малая постоянная времени контура положения есть 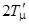 , и тогда передаточная функция разомкнутого контура положения
, и тогда передаточная функция разомкнутого контура положения
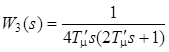 .
.
Из структуры (рис. 4.2) видно, что
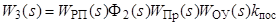 . (4.6)
. (4.6)
Из (4.6) выразим W РП(s)
 . (4.7)
. (4.7)
После подстановки в (4.7) значений всех передаточных функций получим передаточную функцию регулятора положения
 , (4.8)
, (4.8)
где 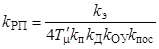 - коэффициент передачи регулятора положения.
- коэффициент передачи регулятора положения.
Анализ выражений передаточных функций регуляторов тока (4.1), ЭДС (4.5) и положения (4.8) показывает, что настройка регулятора тока зависит от задаваемого коэффициента передачи усилителя k У, настройка регулятора ЭДС не зависит от k У и параметров ОУ, а настройка регулятора положения определяется параметрами объекта и коэффициентом передачи пропеллера k п. Учитывая, что вблизи горизонтального положения платформы (α0 = 90°) коэффициент передачи пропеллера k п меняется незначительно, рекомендуется применять усредненное постоянное значение k п, полученное в ходе исследования механического объекта [2].
Таким образом, для реализации трехконтурной системы регулирования и последующего ее исследования необходимо рассчитать и настроить регуляторы контуров в соответствии с заданием, в котором указывается значение коэффициента передачи усилителя k У и рабочая точка α = α0, для которой ранее были получены параметры ОУ: k ОУ, T ОУ и ζ.
В соответствии со схемами регуляторов, представленных на лицевой панели макета, и выражениями передаточных функций (4.1) и (4.8) расчет настраиваемых параметров производится следующим образом. Для регулятора тока (4.1) имеем
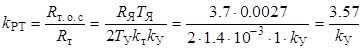
откуда при известном значении R т. о. с, указанном на лицевой панели, определяем R т, соответствующее заданному k У:
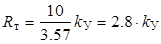 [кОм].
[кОм].
Поскольку постоянная времени регулятора, равная Т Я, не изменяется, значения сопротивления 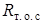 и емкости С т выбраны в соответствии с
и емкости С т выбраны в соответствии с 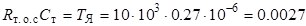 с.
с.
Для регулятора положения (4.8) имеем 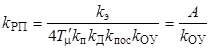 ,
,
где  - при принятых допущениях величина постоянная.
- при принятых допущениях величина постоянная.
В соответствии со схемой регулятора положения имеем 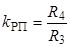 , откуда
, откуда  .
.
Значения R 1 и R 2 определяются следующими соотношениями:
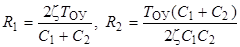 .
.
Значение сопротивления R 4 выбрано в соответствии с выражением 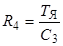 .
.