Разнообразие материалов и методов формирования полупроницаемых мембран, а также возможных сфер их применения требует создания стандартных методик оценки их структуры и технологических свойств. Однако сегодня ситуация такова, что единой и универсальной методики не существует. Это объясняется различным теоретическим подходом к объяснению массопереноса, а также различной интерпретацией результатов измерений.
Характеризуя каждую конкретную мембрану, можно говорить о ее структуре и о технологических параметрах.
Структура мембраны - это макрохарактеристика ее с точки зрения наличия, количества, размера пор. Конкретно структура мембраны оценивается пористостью, размером пор и распределением пор по размерам. К технологическим параметрам относятся удельная производительность, селективность, соответствующие характеристики диффузионных мембран.
Общая пористость
Пористость П - это доля объема твердого тела, не заполненного его материалом.
П = Vc/V = 1- Vt/V (4.19)
Другой признак, по которому твердое тело относится к пористым системам, - это дискретность свободного объема. Иными словами свободный объем разделен на простейшие структурные элементы - поры, отличающиеся размером, формой, характером связи между собой. Чаще поры формируют непрерывную в пределах мембраны открытую пористую структуру, иногда поры изолированы друг от друга.
В реальной мембране поры могут быть сквозными, т.е. пронизывающими всю толщу материала, тупиковыми и полостными.
По генезису все пористые материалы, и мембраны тоже, делятся на системы сложения ( корпускулярные структуры) и системы вычитания (губчатые структуры). Образование первых происходит сложением большого числа отдельных элементов структуры (ткани, бумаги, керамика, углерод, металлы). Развитие структур вычитания - результат превращений, пиролитического разложения, выщелачивания и т.п. компонентов твердого тела (пористые стекла, полимерные мембраны, трековые мембраны и др.).
Поры в системах сложения представляют собой промежутки между частицами, соединяющиеся в извилистые пересекающиеся каналы с переменным диаметром. Анизотропия мембран обусловлена только разным размером частиц.
Поры в системах вычитания представляют собой лабиринтную сеть каналов между глобулами, пачками, кристаллитами твердой фазы. Анизотропия мембран обусловлена числом, ориентацией и размером пор.
Рассмотрим способы оценки пористой структуры. Она оценивается рядом параметров, в зависимости от назначения материала: суммарным объемом, общей пористостью, удельной поверхностью, средним или максимальным размером пор и распределением пор по размерам.
Общая пористость выражается в процентах и часто не коррелируется с транспортными свойствами мембран из-за наличия закрытых и тупиковых пор. Поэтому иногда для мембран вводят понятие "эффективная" пористость. Экспериментальное определение эффективной пористости очень затруднено и оценивается косвенными методами. Общая пористость П может быть рассчитана, если известен элементный состав мембраны:
m a aп
П = [ 1 - — (— + … + —) ] 100% (4.20)
V ρ1 ρп
где m - масса образца; V - общий его объем; a – доля составного элемента; ρ – его плотность.
Наиболее простой способ измерения П - это пропитка образца абсолютно смачивающей жидкостью и определение массы до и после пропитки
mk – m0
————
mk – m0 ρж
П = ———— 100% = ———————— 100% (4.21)
V ρж mk – m0 m0 ———— + ——
ρж ρт
где ρж- плотность жидкого; ρт - плотность твердого состояния образца.
Обычно общая пористость асимметричных полимерных мембран составляет 60-80%, трековых мембран - 2-10%, неорганических мембран - 20-50%.
Общую пористость мембран, находящихся в набухшем состоянии, определяют в обратном порядке, т.е. сначала определяют массу набухшего, а потом высушенного образца.
Размер пор
Все методы исследования пористой структуры можно разделить на транспортные, связанные с переносом жидкости или газа через мембрану, и нетранспортные. В любом случае нельзя забывать, что реальные поры очень сильно отличаются от идеализированных пор, которые положены в основу различных моделей мембран (рис.4.62).

Рис. 4.62. Сравнение идеальной и реальной структуры разделительного слоя пористой мембраны
1. Электронная микроскопия
Различают два варианта такого анализа - сканирующая электронная микроскопия (СЭМ) и трансмиссионная или просвечивающая (ТЭМ). Первый вариант более прост и информативен, поэтому используется чаще. На рисунке 4.63 дана принципиальная схема СЭМ.

Рис. 4.63. Принципиальная схема сканирующей электронной микроскопии
Узкий пучок электронов направляется на исследуемый образец. Эти электроны называются первичными и имеют высокую энергию - до 25 кV. От поверхности образца отражаются вторичные низкоэнергетические электроны, которые выбиваются первичными из электронных оболочек атомов образца. Узкий пучок первичных электронов перемещают построчно по образцу, ощупывая (сканируя) его поверхность. Вторичные электроны улавливают, усиливают, преобразуют в электрический сигнал и реконструируют в изображение на экране.
Для получения лучшей контрастности поверхность образца подтеняют слоем металла (Cr, Рt, Аu, Рd и др.). Иногда, если изучаемый материал неустойчив под действием электронного пучка, после покрытия металлом изучаемой поверхности, т.е. получения слепка (реплики), материал удаляют растворением и исследуют реплику.
Иногда для отверждения образца используют криометод, т.е. образец быстро замораживают жидким азотом, а лед сублимируют под вакуумом.
Среди трудностей, связанных с использованием электронной микроскопии для изучения пористой структуры мембран, необходимо указать на возможность изменения последней при высушивании и замораживании образцов, а также на сложность получения их ультратонких срезов, что приводит к неадекватности исследуемой структуры первоначальной. Полностью избежать указанных изменений, по всей видимости, невозможно, поэтому электронная микроскопия, несмотря на очевидные достоинства, не может быть признана абсолютным и исчерпывающим методом анализа пористой структуры мембран.
2.Ртутная порометрия
Метод основан на том, что жидкость, не смачивающая твердое тело, проникает в его поры лишь при воздействии внешнего давления. Объем жидкости, проникшей в поры, является функцией давления, что позволяет судить о распределении пор по размерам. Самой не смачивающей жидкостью является ртуть, поэтому ее и используют.
Ртутно-порометрические установки содержат два основных узла: систему создания давления для внедрения ртути в объемы пор и систему измерения объема вдавленной в поры ртути. Все установки снабжены также оборудованием для вакуумирования образца перед измерением. Расчет результатов основан на уравнении Лапласа:
2 σ
r = −−− cos θ (4.22)
P
где σ – поверхностное натяжение ртути; Р – давление; θ – краевой угол смачивания материала ртутью.
Поскольку угол смачивания материала мембран ртутью почти всегда 141°, а поверхностное натяжение ртути 0,48 Н/м, то расчетное уравнение упрощается:
R = 7492/∆P (4.23)
На рисунке 4.64 представлен типичный результат измерения.

Рис4.64. Объем поглощенной ртути как функция приложенного давления
При низком давлении заполняются большие поры, затем все более мелкие согласно уравнению Лапласа. При достижении насыщения можно по кривой рассчитать и распределение пор по размерам.
3.Метод "точка пузырька"
Метод относится к группе транспортных и определяет только сквозные поры, в то время как предыдущие позволяли обнаружить и тупиковые, и даже замкнутые поры. Поэтому с его помощью можно характеризовать пористую структуру разделительного слоя мембраны, правда, только со стороны крупных пор.
Метод "точка пузырька" был разработан Бехольдом в начале века. Схема аналитической установки показана на рисунке 4.65.

Рис. 4.65. Схема установки для определения максимального размера пор в мембране:
1-верхняя крышка; 2-металлическая сетка; 3-мембрана; 4-пористая подложка; 5-корпус ячейки; 6-регулирующий вентиль;7-прокладки; 8-емкость с водой; 9-пузырек воздуха.
В измерительную ячейку помещают исследуемую мембрану и заливают слой жидкости высотой 3-5 мм, обычно воду. Затем начинают ступенчато повышать давление сжатого газа, регулируя его с помощью вентиля 6 и выдерживая 1-2 мин. на каждой ступени, до проскока первого пузырька 9 через мембрану. На рис.4.66 представлено изображение происходящего процесса.

Рис. 4.66. Принцип метода "точка пузырька"
Связь между давлением и радиусом поры, через которую прорвался пузырек, дается уравнением Лапласа:
2 σ
rn = −−− cos θ (4.24)
∆P
Расчет ведут при допущениях, что пора имеет правильную цилиндрическую форму и смачиваемость мембраны жидкостью абсолютная (cos θ =1). Тогда для системы вода-воздух получается примерно такое соотношение:
| Р,бар | 0,14 | 1,4 | 14,5 | |
| d,мкм | 1,0 | 0,1 | 0,01 |
Для понижения давления иногда заменяют воду жидкостью с малым поверхностным натяжением, чаще всего изопропанолом, если в нем не набухает мембрана. Нетрудно убедиться, что для одного и того же значения точки пузырька рассчитанный размер пор в предположении их круглого сечения больше, чем для эллипсоподобного, что приводит к завышению размеров реальных пор, сечение которых ближе по форме к эллипсу.
Определенную погрешность в оценку размеров пор вносит и допущение об идеальной смачиваемости мембран (соs θ =1). Тем не менее, доступность метода "точки пузырька" позволяет широко использовать его для первичной характеристики мембран и проверки их целостности. Иногда в каталогах дают коэффициент соотношения rmax/rcp, для оценки этим методом rcp.
4. Проточная порометрия
Перенос жидкости или газа через пористую среду связан с параметрами этой среды. Проточный метод изучения пористой структуры основан на зависимости удельной производительности от параметров пористости. Расчет основан на уравнении Пуазейля:
π r4∆P
V = ———— (4.25)
8ηδ
Модель упрощена до представления мембраны как пористого тела с прямыми цилиндрическими порами. Реальность поры, т.е. ее извилистость, шероховатость, анизотропность, учитывается эмпирическими коэффициентами.

Рис. 4.67. Ячейка для определения среднего размера пор в мембранах:
1-верхняя крышка;
2-уплотнителъное кольцо;
3-мембрана;
4-пористая подложка;
5-сетка; 6-нижняя крышка;
7-корпус ячейки;
8-уплотнительная прокладка (резиновое кольцо)
Для стандартизации условий испытаний используют ячейки с постоянной площадью мембраны (рис.4.67). На дно нижней крышки 6 помещают металлическую сетку 5, затем подложку 4, испытываемую мембрану 3, уплотнительное кольцо 2. Толщину мембраны предварительно измеряют микрометром. Регулируют давление сжатого воздуха и измеряют производительность образца по жидкости, заливаемой в ячейку.
Если бы поры в мембране были все одинаковы, мы имели бы графическую зависимость проницаемости от давления как на левой части рис.4.68. Сначала мембрана остается непроницаемой, поскольку для продавливания жидкости через любую пору необходимо некоторое давление. Величина Рmin определяется смачиваемостью мембраны жидкостью и размером самых больших пор.

Рис. 4.68. Зависимость удельной производительности мембраны от приложенного давления для идеальной (слева) и реальной (справа) мембраны
В реальной мембране всегда существует некоторое распределение пор по размерам, поэтому кривая проницаемости сначала имеет S-образный участок, а затем линейный. Уравнение Пуазейля можно записать для выражения количества жидкости, прошедшей через мембрану площадью S с числом пор N на единице площади за время t:
π r4∆PtSN
V = ————— (4.26)
8ηδ
В свою очередь N = П/ π r3, где П - общая пористость мембраны, отсюда
8 ηδV 8 ηG
r = ————— = ———— (4.27)
П∆PtS П∆P
Расчет, проведенный по данным линейного участка зависимости на рис.4.68, даст величину среднего размера пор мембраны, что для мембран с узким распределением пор является достаточной характеристикой.
Принимаемые в методе допущения (о цилиндричности и неизвилистости пор, постоянстве сечения по всей длине отдельных пор, равенстве общей и эффективной, т.е. участвующей в транспорте жидкости, пористости мембраны) вносят определенные погрешности в оценку среднего размера пор ультрафильтрационных мембран. В частности, извилистость реальных пор приводит при расчетах к заниженным значениям их размеров. К заниженным результатам приводит и различие в общей и эффективной пористости мембран вследствие ориентационной упорядоченности пор.
К уменьшению величины эффективной пористости по сравнению со значениями, используемыми в расчетах, а, следовательно, и занижению результатов, приводит наличие в мембранах не участвующих в течении пристенных слоев связанной воды.
Толщина таких гидродинамически неподвижных слоев составляет примерно 1 нм и, следовательно, вклад этого фактора становится весьма ощутимым для сравнительно тонкопористых мембран.С другой стороны, асимметрия структуры мембраны приводит к завышенным значениям средних размеров пор. Это в определенной мере нивелирует их занижение вследствие неучета пристенных слоев воды, извилистости и ориентационной упорядоченности пор.
Итак, в реальной мембране существуют поры разного размера, поэтому зависимость G от ΔР на рисунке 4.67 имеет S-образный характер, т.е. по мере повышения давления в работу включаются все меньшие поры. Если проводить ступенчатое по ΔР исследование, то на каждый прирост ΔР наложится прирост в G (рисунок 4.69).
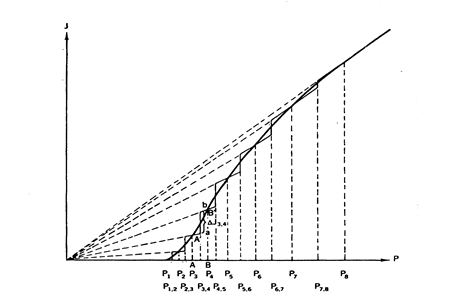
Рис. 4.69. Графическая дифференциация зависимости удельной производительности мембраны от приложенного давления
В расчете будем использовать модифицированные уравнения Пуазейля и Лапласа:
π∙r4i-j t ∙ S ∙ Ni-j
Vi-j = ────────── ∙ Pj (4.28)
8 ηδ
Pj = 2σ/ri-j (4.29)
Из них получим расчетные выражения для r и N:
r ∙ δ
Ni-j = ──── ∙ P3j ∙ΔGi-j (4.30)
2πσ4
ri-j = 2σ/Pj (4.31)
Рассчитав для каждого интервала i-j эти две величины, получим информацию для построения зависимости Ni-j для каждого интервала ri-j (рис. 4.70).

Рис. 4.70. Зависимость «количество пор – радиус пор»,
т.е. кривая распределения пор по размеру
Распределение пор по размеру является наиболее объективной характеристикой пористой мембраны.