Проверим соответствие эмпирического распределения объема предоставляемых кредитов за 2006 год нормальному распределению на основе критерия согласия Пирсона. Данная информация представлена в приложении В.
Таблица 2.1.5- Предоставленные кредиты
| Кредиты, предоставленные в рублях | Объем кредита млн.руб 2006 г. | |
| Всего | 4 220 325 | |
| из них по срокам погашения до 30 | 245 457 | |
| 31-90 | 247 377 | |
| 91-180 | 362 185 | |
| 181-365 | 966 959 | |
| 365-1095 | 792 270 | |
| Свыше 1095 | 303 460 |
Выдвинем нулевую гипотезу о том, что изучаемая совокупность распределена нормально.
Для этого вычислим теоретические частоты 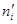 и величину критерия
и величину критерия
Пирсона 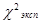
Критерий согласия Пирсона 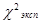 определяется выражением:
определяется выражением:
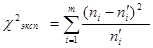 ,
,
где ni – эмпирические (наблюдаемые) частоты,
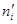 - теоретические (выравнивающие) частоты, рассчитываются
- теоретические (выравнивающие) частоты, рассчитываются
по формуле:
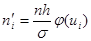 ,
,  ,
, 
где xi – середина интервала,
h –ширина интервала.
Сначала найдем величины средней арифметической и среднеквадратического отклонения для исходного интервального вариационного ряда.
Таблица 2.1.6-Расчеты для вычисления обобщающих показателей и показателей вариации
| xi | ni | xi* ni | 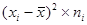
| S |
| 245 457 | ||||
| 247 377 | ||||
| 362 185 | ||||
| 966 959 | ||||
| 792 270 | ||||
| Итого |
Средняя величина:
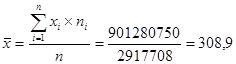
Среднеквадратическое отклонение:

Далее вычислим 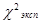 ,для этого составим таблицу для проведения промежуточных расчетов.
,для этого составим таблицу для проведения промежуточных расчетов.
Таблица 2.1.7- Расчеты для вычисления 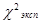
| хi | ni | ui | φ(ui) | 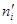
| 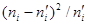
|
| 245 457 | -0,86 | 0,2756 | 5035,8 | ||
| 247 377 | -0,82 | 0,2850 | |||
| 362 185 | -0,78 | 0,2943 | |||
| 966 959 | -0,67 | 0,3187 | |||
| 792 270 | -0,009 | 0,3989 | |||
| 3,17 | 0,0042 | ||||
| Итого | 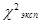 =2858346 =2858346
|
Исходя из данных, получаем 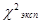 =2858346
=2858346
По таблице «Критические точки распределения Пирсона  » при заданном уровне значимости α и числе степеней свободы ν находим
» при заданном уровне значимости α и числе степеней свободы ν находим 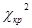 .
.
Примем уровень значимости α=0,05. Число степеней свободы:
ν=s-k-1,
где s- число групп;
k- число параметров распределения.
Ν=6-2-1=3
Тогда 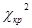 =7,81
=7,81
Сравнивая экспериментальное и критическое значения критерия Пирсона, получаем что 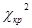 <
< 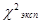 . Из этого следует вывод, что изучаемая совокупность распределена ненормально.
. Из этого следует вывод, что изучаемая совокупность распределена ненормально.
Таким образом, рассматриваемая совокупность объема предоставляемых кредитов на 2006 год не подчиняется нормальному закону распределения.
Для исходных данных рассчитаем моду и медиану по следующим формулам:
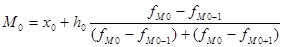
где х0-нижняя граница модального интервала;
h0- величина модального интервала;
fM0- частота модального интервала;
fM0-1-частота интервала, предшествующего предыдущему;
fM0+1- частота интервала, следующего за модальным.
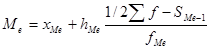
где хМе- нижняя граница медианного интервала;
hМе- величина медианного интервала;
fMе- частота медианного интервала;
SMe-1- накопленная частота интервала, предшествующего медианному.
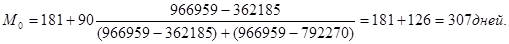
Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто. Из этого следует, что в совокупности предоставления кредита самым распространенным является срок погашения 307 дней.
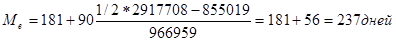
Медиана- величина изучаемого признака, которая находится в середине упорядоченного ряда. Таким образом, 50% объема кредита погашается менее чем за 237 дней, а другие 50% - более чем за 237 дней.