Тема: Определение транспортных издержек при перевозке груза. Решение оптимизационных задач в Excel
Цель: Научиться решать и определить транспортные издержки при перевозке груза с помощью оптимизационных задач в Excel
Краткие теоретические сведения
Решение оптимизационных задач в Excel
Пример 1 Транспортная задача.
Груз, хранящийся на двух складах (A и B) и требующий для перевозки 20 и 30 автомашин соответственно, необходимо перевезти в три магазина. Первому магазину требуется 10 машины груза, второму – 30 и третьему – 10. Стоимости перевозки одной автомашины указаны в следующей таблице:
| Склады | Магазины | ||
| A | |||
| B | |||
Требуется составить оптимальный по стоимости план перевозки груза от складов до магазинов.
Решение задачи
1. Подготовка задачи к решению
Пусть xij количество автомашин перевезенных из пунктов (склады А и В) отправления в пункты назначения (магазины 1, 2 и 3);
Тогда система ограничений и целевая функция (транспортные расходы) запишутся следующим образом:
4x11 + 9х12 + 3х13 +4х21+8 х22+x23Þ min (целевая функция);
| x11 + х21 =10 | Все потребности магазинов должны быть удовлетворены | |
| x12 + х22=30 | ||
| x13 + х23=10 | ||
| x11 + х12 + х13 =20 | Все запасы должны быть исчерпаны | |
| X21 + х22 +х23 =30 |
2. Подготовка рабочей книги.
Для решения задачи в Excel запишем ее в виде, представленном на рис. 2.1.
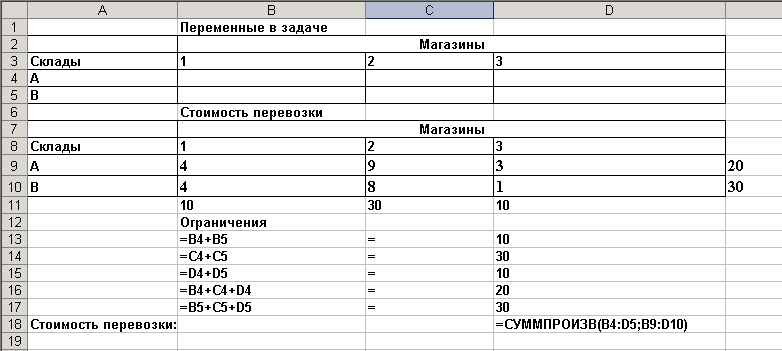
Рисунок 2.1 – Вид рабочего листа Excel
Далее вызываем Поиск решения из меню Сервис.
Определяем целевую ячейку (в нашем случае D18), устанавливаем переключатель в минимальное значение. Вводим диапазон изменяемых ячеек ($B$4:$D$5) и вносим ограничения.
Прежде всего, количество перевозимого груза не может быть отрицательным ($B$4:$D$5$>= 0), далее добавляем ограничения на потребности и запасы груза, которые должно быть равны требуемым (В$13=D$13), и т.д. по всем ограничениям.
Нажимаем кнопку Выполнить и получаем следующий оптимальный план перевозки груза, представленный в таблице.
| Склады | Магазины | ||
| A | |||
| B |
Пример 2. Задача линейного программирования.
Рассмотрим в качестве примера мебельную фабрику, производящую столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены в таблице:
| Столы | Стулья | Объем ресурсов | |
| Расход древесины на изделие, м3 | 0,5 | 0,04 | |
| Расход труда, человеко-часов | 0,6 | ||
| Прибыль от реализации единицы изделия, руб. |
Кроме того, на производство 80 столов заключен контракт с муниципалитетом, который должен быть безусловно выполнен. Необходимо найти такую оптимальную производственную программу, чтобы прибыль от реализации продукции была максимальной.
Пусть x1 - количество столов;
х2 - количество стульев.
Тогда система ограничений и целевая функция запишутся следующим образом:
180x1 + 20х2 Þ max (целевая функция, выражающая планируемую прибыль в рублях от реализации всего объема продукции);
0.5x1 + 0.04х2  200 (ограничения по имеющемуся объему древесины);
200 (ограничения по имеющемуся объему древесины);
12x1 + 0.6х2  1800 (ограничения по доступному объему трудовых ресурсов);
1800 (ограничения по доступному объему трудовых ресурсов);
x1 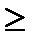 80 (контракт с муниципалитетом);
80 (контракт с муниципалитетом);
x1 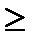 0; х2
0; х2 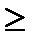 0;
0;
x1, х2 - целые числа.
Для подготовки к решению задачи в Excel запишем ее в виде, представленном на рис. 2.4
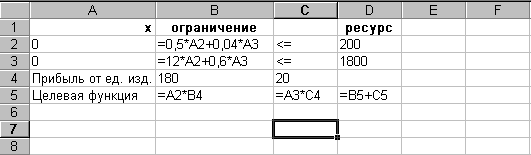
Рисунок 2.2 – Запись исходных данных для решения задачи линейной оптимизации
Для решения задачи вызовем меню Сервис-Поиск решения.
В открывшемся диалоговом окне Поиск решения (рис. 2.5) укажем:
- адрес целевой ячейки (в нашем примере D5);
- диапазон искомых ячеек (А2:A3);
ограничения: А2>=80
A2:A3=целое
A2:A3>=0
В2<=D2
B3<=D3.
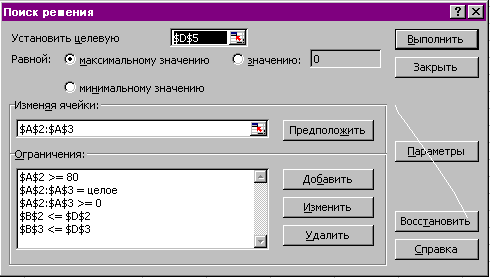
Рисунок 2.3 – Диалоговое окно Поиск Решения
Добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить, Изменить, Удалить.
Для нахождения оптимального решения нажмем кнопку Выполнить. В результате в ячейке таблицы получим значение целевой функции – 42400 рублей при x1 = 80 и x2 = 1400.
Как видно из результатов решения, предприятию производить столы не очень выгодно. Поэтому оно ограничило объем их выпуска в количестве, необходимом для выполнения контракта. Остальные ресурсы направлены на производство стульев.
Диалоговое окно «Параметры поиска решения» позволяет изменять условия и варианты поиска решения для линейных и нелинейных задач, а также загружать и сохранять оптимизируемые модели.
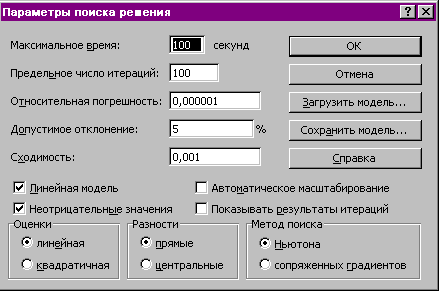
Рисунок 2.4 – Диалоговое окно Параметры поиска решения
Диалоговое окно Результаты поиска решения позволяет:
– сохранить на текущем рабочем листе найденное оптимальное решение;
– восстановить первоначальные значения;
– сохранить сценарий;
– выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения.
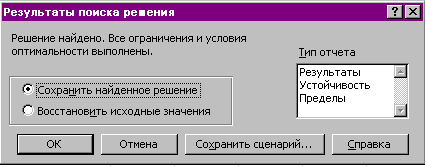
Рисунок 2. 5 – Диалоговое окно Результаты поиска решения
Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями.
Пример 3 Задача о диете.
Фирма занимается составлением диеты, содержащей, по крайней мере, 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при известных ценах имеющихся продуктов?
| Хлеб | Соя | Рыба | Фрукты | Молоко | |
| Белки | |||||
| Углеводы | |||||
| Жиры | |||||
| Витамины | |||||
| Цена на 1кг или 1литр продукта |
Решение задачи
1. Подготовка задачи к решению
Пусть x1 - количество хлеба в составе диеты;
х2 - количество сои в составе диеты;
x3 - количество рыбы в составе диеты;
x4.-. количество фруктов в составе диеты;
x5.-. количество молока в составе диеты;
Тогда система ограничений и целевая функция запишутся следующим образом:
12x1 + 36х2 + 32х3 +18х4+10 х5Þ min (целевая функция);
2x1 + 12х2 + 10х3 +х4+2 х5 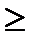 20 20
| ограничения на количество | |
12x1 + 4х4+3 х5 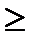 30 30
| питательных веществ(белков, | |
x1 + 8х2 + 3х3+4 х5 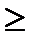 10 10
| углеводов, жиров, витаминов) | |
2x1 + 2х2 + 4х3 +6х4+2 х5 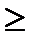 40 40
| в рационе |
x1 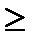 0; х2
0; х2 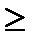 0; x3
0; x3 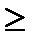 0; х4
0; х4 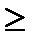 0; x5
0; x5 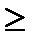 0;
0;
Расчет питательных веществ (белков, углеводов, жиров, витаминов) осуществляется по формуле:
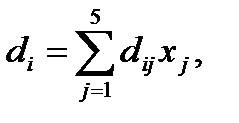
где di – расчетное количество i-го питательного вещества;
xj – расчетное количество j-го продукта в рационе.
2. Подготовка рабочей книги.
Для решения задачи нам необходимо сначала подготовить рабочую книгу.
Создадим на рабочем листе таблицу с исходными данными и поместим в нее названия продуктов и данные по содержанию в них питательных веществ, а также укажем цены продуктов.
После этого создадим таблицу для поиска решения, в которую включим название продукта, его количество в рационе (диете) и стоимость данного рациона.
| Хлеб | Соя | Рыба | Фрукты | Молоко | Цена |
Общая Цена определяется произведением Количество х Цена
Для того, чтобы сравнить рассчитанную диету с нормой по питательным веществам, под строкой таблицы исходных данных, содержащей норму питательных веществ, добавим таблицу, отражающую соответствие питательных веществ в расчетном рационе (диете).
| Нужно | Получено | |
| Белки | 20 | |
| Углеводы | 30 | |
| Жиры | 10 | |
| Витамины | 40 |
После проделанного, лист в Excel будет выглядеть следующим образом
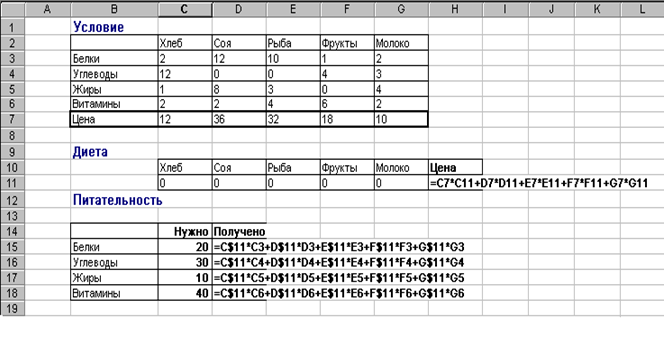
Рисунок 2. 7 – Запись исходных данных для решения задачи линейной оптимизации
3. Поиск решения
В соответствии с условием, критерием оптимальности диеты, кроме определенного содержания белков, жиров, углеводов и витаминов, будет еще и минимальная стоимость. Поэтому в таблицу добавлено поле Цена для расчета наименьшей стоимости дневного рациона (диеты). В нем будут суммироваться стоимости продуктов дневного рациона.
Далее вызываем Поиск решения из меню Сервис.
Определяем целевую ячейку (в нашем случае Н11), устанавливаем переключатель в минимальное значение. Вводим диапазон изменяемых ячеек ($C$11:$G$11) и вносим ограничения.
Прежде всего, количество продукта в рационе не может быть отрицательным ($C$11:$G$11>= 0). Далее добавляем ограничения на количество питательных веществ в рационе, которое должно быть не менее нормативного (D$16>=C$16), и т.д. по всем питательным веществам.
Нажимаем кнопку Выполнить и получаем решение задачи.

Рисунок 2. 8 – Вид рабочего листа Excel с решенной задачей
Задания
Вариант 1 и 16
Задание 1. Транспортная задача.
Запишите целевые функции, составьте системы ограничений и найдите средствами Excel оптимальное решение, удовлетворяющее условиям задания.
В пунктах A и B находятся соответственно 150 и 90 т горючего. Пунктам 1, 2, 3 требуются соответственно 60, 70, 110 т горючего. Стоимость перевозки 1 т горючего из пункта A в пункты 1, 2, 3 равна соответственно 60, 10, 40 д. ед. за 1 т соответственно, а из пункта B в пункты 1, 2, 3 – 120, 20, 80 д. ед. за 1 т соответственно.
Составьте план перевозок горючего, минимизирующий общую сумму транспортных расходов.
Задание 2. Модели линейного программирования.
Небольшое предприятие выпускает два типа автомобильных деталей. Для этого оно покупает отливки, которые подвергаются токарной обработке, сверловке и шлифовке. Данные характеризующие производительность станочного парка предприятия, приведены в таблице
| Станки | Деталь А, дет/час | Деталь В, дет/час | Стоимость часа работы |
| Токарные | |||
| Сверлильные | |||
| Шлифованные | 17,5 |
Каждая отливка, из которой изготавливают деталь А, стоит 2 д. ед., стоимость отливки для детали В – 3 д. ед. Продажная цена деталей равна соответственно 5 и 6 д. ед.
Определить план выпуска продукции, максимизирующей прибыль предприятия, в условиях, когда для продажи возможно выпускать любую комбинацию деталей А и В.
Вариант 2 и 17
Задание 1. Транспортная задача.
Три завода выпускают грузовые автомобили, которые платформами отправляются четырем потребителям. Первый завод поставляет 90 платформ грузовиков, второй – 30 платформ, третий – 40 платформ. Требуется поставить платформы следующим потребителям: первому – 70 штук, второму – 30, третьему – 20, четвертому – 40 штук.
Стоимость перевозки одной платформы от поставщика до потребителя указана в следующей таблице (д.е.):
| Поставщики | Потребители | |||
| 1 | 2 | 3 | 4 | |
| I | ||||
| II | ||||
| III |
Составьте оптимальный план доставки грузовых автомобилей
Задание 2. Модели линейного программирования.
Фирма производит изделия двух типов. Производственные мощности позволяют выпустить в сутки не более 100 изделий типа 1 и не более 300 изделий типа 2. Наличие сырья позволяет выпустить в сутки не более 150 изделий любого типа, причем изделия типа 1 дает прибыль в 2 раза больше по сравнению с изделием типа 2.
Определить план выпуска изделий, максимизирующую суточную прибыль фирмы.
Вариант 3 и 18
Задание 1. Транспортная задача.
Строительство магистральной дороги включает заполнение грунтом имеющихся на трассе выбоин до уровня основной дороги и срезания в некоторых местах дороги выступов. Выбоины заполняются срезанным грунтом. Перевозка грунта осуществляется грузовиками грузоподъемностью в 5 тонн.
Расстояние в километрах от мест срезов до мест выбоин и объем работ указаны в следующей таблице:
| Поставщики грунта | Потребители грунта | Наличие грунта, т | ||
| I | II | III | ||
| А | ||||
| В | ||||
| С | ||||
| Требуемое количество грунта, т |
Составьте план перевозок, минимизирующий общий пробег грузовиков. Изменится ли план перевозок, если для перевозки грунта будут использованы грузовики грузоподъемностью 7 тонн?
Задание 2. Модели линейного программирования.
Фирма производит краску двух видов, причем прибыль от реализации одной тонны краски А составляет 3 тыс. д. ед., а краски В составляет 2 тыс. д. ед.
Для производства краски используются 2 продукта.
| Продукт | Расход продукта на 1 тонну краски | Суточный запас продукта/тонн | |
| краска А | краска В | ||
Анализ рынка сбыта показал, что суточный спрос на краску В никогда не превышает спрос на краску А более чем на 1 тонну, кроме того спрос на краску В никогда не превышает 2 тонны в сутки.
Определить суточный план производства краски, максимизирующий прибыль фирмы.
Вариант 4 и 19
Задание 1. Транспортная задача.
Груз, хранящийся на трех складах и требующий для перевозки 60, 80, 106 автомашин соответственно, необходимо перевезти в четыре магазина. Первому магазину требуется 44 машины груза, второму – 70, третьему – 50 и четвертому – 82 машины. Стоимость пробега одной автомашины за 1 км составляет 10 д.е. Расстояния от складов до магазинов указаны в следующей таблице:
| Склады | Магазины | |||
Составьте оптимальный по стоимости план перевозки груза от складов до магазинов.
Задание 2. Модели линейного программирования.
Фирма производит электровыключатели типов 1 и 2. Трудоемкость изготовления выключателей типа 1 вдвое больше трудоемкости изготовления выключателей типа 2.
Если бы фирма производила только выключатели типа 2, то суточный объем производства мог бы составить 1000 выключателей. Суточная поставка медного провода обеспечивает изготовление не более 800 выключателей двух типов.
Для изготовления выключателей требуются специальные изоляторы, причем для выключателя типа 1 их можно получить не более 400 штук в сутки, а для выключателя типа 2 не более 700 штук в сутки.
Определить план производства электровыключателей, максимизирующий суточную прибыль фирмы, если удельная прибыль составляет соответственно 4 и 3 д. ед.
Вариант 5 и 20
Задание 1. Транспортная задача.
На складах А, В, С находится сортовое зерно 100, 150, 250 т, которое нужно доставить в четыре пункта. Пункту 1 необходимо поставить 50 т, пункту 2 – 100, пункту 3 – 200, пункту 4 – 150 т сортового зерна. Стоимость доставки 1 т зерна со склада А в указанные пункты соответственно равна 80, 30, 50, 20; со склада В – 40, 10, 60, 70; со склада С -10, 90, 40, 30 денежных единиц.
Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки.
Задание 2. Модели линейного программирования.
Фирма планирует выпуск мужских и женских костюмов. На мужские костюмы требуется 3,5 м шерсти; 0,5 м лавсана и 1 человеко-день трудозатрат.
На женский костюм – 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат.
В наличии имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат.
План предусматривает выпуск не менее 110 костюмов, причем необходимо обеспечить прибыль не менее 1400 д. ед.
Определить план производства костюмов, максимизирующий прибыль фирмы. Если прибыль от реализации мужских костюмов – 20 д. ед., женских костюмов –
10 д. ед.
Вариант 6 и 21
Задание 1. Транспортная задача.
Завод имеет три цеха – А, В, С и четыре склада – 1; 2; 3; 4. Цех А производит 30 тыс. шт. изделий, цех В – 40; цех С – 20 тыс. шт. изделий. Пропускная способность складов за то же время характеризуется следующими показателями: склад 1 – 20 тыс. шт. изделий; склад 2 – 30; склад 3 – 30 и склад 4 – 10 тыс. шт. изделий. Стоимость перевозки 1 тыс. шт. изделий из цеха А на склады 1, 2, 3, 4 – соответственно: 20, 30, 40, 40; из цеха В – соответственно 30, 20, 50, 10; а из цеха С – соответственно 40, 30, 20, 60 денежных единиц.
Составьте такой план перевозки изделий, при котором расходы на перевозку
90 тыс. шт. изделий были бы наименьшими.
Задание 2. Модели линейного программирования.
Радиозавод выпускает магнитофоны двух моделей: A и B. Завод должен выпускать в месяц не менее Мa и Мв магнитофонов. Каждая модель приносит доход в размере Дa и Дв рублей. Процесс производства магнитофонов состоит из трех стадий: изготовления деталей, сборки изделия и его упаковки. Нормативы времени на эти стадии заданы в таблице. Производственные мощности завода позволяют расходовать в месяц не более 600 часов на выпуск деталей, 500 часов на сборку магнитофонов и 200 часов на упаковку.
| Дa | Дв | Мa | Мв | Нормативы времени (часов на 1 шт) | |||
| Модель | Стадия 1 | Стадия 2 | Стадия 3 | ||||
| 0.3 | 0.4 | 0.1 | |||||
| 0.35 | 0.5 | 0.15 |
Составить план выпуска магнитофонов, обеспечивающий заводу максимальный доход. Определить, какая из стадий в наибольшей степени сдерживает рост производства.
Вариант 7 и 22
Задание 1. Транспортная задача.
Имеются две станции технического обслуживания (СТО), выполняющие ремонтные работы для трех автопредприятий. Производственные мощности СТО, стоимость ремонта в различных СТО, затраты на транспортировку от автопредприятий на СТО и обратно и прогнозируемое количество ремонтов в планируемом периоде на каждом автопредприятии приведены в следующей таблице:
| СТО | Стоимость ремонта ед.,д.е. | Затраты на транспортировку, тыс. руб. | Производственная мощность, шт. | ||
| АТП-1 | АТП-2 | АТП-3 | |||
| Потребное количество, шт |
Требуется определить, какое количество автомашин из каждого автопредприятия необходимо отремонтировать на каждой СТО, чтобы суммарные расходы на ремонт и транспортировку были минимальными.
Задание 2. Модели линейного программирования.
Акционерное общество может возделывать на поле площадью S га. четыре культуры. Наиболее трудоемким этапом является уборка урожая, которая должна осуществляться в два этапа: сначала убираются 1-я и 2-я культуры, а затем 3-я и 4-я. Трудоемкости уборки каждой культуры составляют соответственно Т1, Т2, Т3 и Т4 человеко-часов на 1 га. Для уборки общество может выделить R1 человеко-часов на 1-й этап и R2 на 2-й.
| S | T1 | T2 | T3 | T4 | R1 | R2 | C1 | C2 | C3 | C4 |
Составить план посева культур, дающий максимальную прибыль, если 1 га каждой из культур (при ожидаемой урожайности) приносит прибыль соответственно в С1, С2, С3, С4 (д.ед.). Определить, какой из этапов уборки ограничивает рост прибыли.
Вариант 8 и 23
Задание 1. Транспортная задача.
Имеются две станции с вагонами, в которых сосредоточено 200 и 120 вагонов соответственно. Вагоны необходимо перевезти трем грузополучателям соответственно в количестве 80, 100 и 120 вагонов. Расстояния от станций до подъездных путей грузополучателей следующие:
| Станции | Грузополучатели | ||
Затраты на перевозку 1 вагона на 1 км постоянны и равны 5 д.е.
Определите план перевозок вагонов от станций до подъездных путей грузополучателей из условия минимизации транспортных расходов.
Задание 2. Модели линейного программирования.
Рацион стада крупного рогатого скота из 220 голов включает пищевые продукты А, В, С, D и Е. В сутки одно животное должно съедать не менее 2 кг продукта вида A, 1,5 кг продукта В, 0,9 кг продукта С, 3 кг продукта D и 1,8 кг продукта E. Однако в чистом виде указанные продукты не производятся. Они содержатся в концентратах К-1, К-2 и К-3. Их цена соответственно 0,5; 0,4; 0,9 руб. за килограмм. Содержание продуктов в килограмме концентрата (в %) указано в таблице.
| Концентраты | Продукты | ||||
| A | B | C | D | E | |
| К-1 | |||||
| К-2 | |||||
| К-3 |
Построить модель, на основе которой составить план покупки концентратов при котором затраты на покупку будут минимальны.
Вариант 9 и 24
Задание 1. Транспортная задача.
Станция имеет два ПОП и пять ПНО в различных парках станции. Каждый месяц первые ПОП обрабатывают 50, а второй 70 вагонов. Все вагоны, обрабатываемые ПОП, отправляются ПНО. Вместимость ПНО первого равна 20 вагонов; второго – 30; третьего – 15; четвертого – 27; пятого – 28 вагонов. Издержки транспортировки вагонов от ПОП до ПНО следующие (вагонах):
| ПОП | ПНО | ||||
Распределите план перевозок из условия минимизации ежемесячных расходов на транспортировку.
Задание 2. Модели линейного программирования.
Кондитерская фабрика для производства трех видов карамели A, B и C использует три вида сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья на производство 1 кг карамели заданы в таблице.
| Наименование сырья | Нормы расхода (кг/кг) | ||
| A | B | C | |
| Сахарный песок | 0.6 | 0.5 | 0.6 |
| Патока | 0.4 | 0.4 | 0.3 |
| Фруктовое пюре | 0.1 | 0.2 | 0.2 |
Запасы сырья на складе соответственно равны V1, V2 и V3 кг. Прибыль от реализации 1 кг конфет каждого вида определяется значениями PA, PB и PC.
| Запасы сырья (кг) | Прибыль от реализации (руб./кг) | ||||
| V1 | V2 | V3 | PA | PB | PC |
| 1.08 | 1.12 | 1.28 |
Найти план производства карамели, обеспечивающий максимальную прибыль, при условии, что предприятие должно выпускать не менее 100 кг конфет каждого вида. Выяснить, какое сырье ограничивает рост прибыли, и какую продукцию выпускать наиболее выгодно в данных условиях. Ответ пояснить.
Вариант 10 и 25
Задание 1. Транспортная задача.
Три станции с суточной производительностью 10, 8 и 6 вагонов снабжают три подъездных пути, суточный спрос которых составляет 6, 11 и 7 вагонов. Вагоны отправляются на подъездные пути. Стоимость вагона на 2 км составляет 5 д.е. за 1 вагон. Станция 1 не связана с подъездным путем 3. Расстояние от станции до подъездных путей следующее:
| № станции | № подъездного пути | ||
| - | |||
Сформулируйте соответствующую транспортную задачу и решите ее с учетом требования минимизации транспортных затрат.
Задание 2. Модели линейного программирования.
Мебельная фабрика выпускает столы, стулья, кресла и кровати. При изготовлении этих товаров используется два вида досок. Запасы досок и трудовых ресурсов показаны в таблице.
| Ресурсы | ||
| Доски 1 типа (м) | Доски 2 типа (м) | Трудовые (чел.-час.) |
Нормы расхода сырья, трудоемкость производства продукции и прибыль от реализации единицы продукции показаны в таблице.
| Изделия Ресурсы | Нормы расхода | |||
| Столы | Стулья | Кресла | Кровати | |
| Доски 1 типа (м) | ||||
| Доски 2 типа (м) | ||||
| Трудоемкость (чел.-час.) | ||||
| Прибыль (руб.) |
С учетом спроса на товары фабрика должна выпустить не более 10 кроватей, а соотношение столов и стульев должно быть 1:6.
Найти план производства мебели, дающий фабрике максимальную прибыль.
Вариант 11 и 26
Задание 1. Транспортная задача.
Автомобили перевозятся на трайлерах из трех центров распределения пяти продавцам. Стоимость перевозки в расчете на 1 км пути, пройденного трайлером, равна 60 д.е. Стоимость перевозок не зависит от того, насколько полно загружается трайлер. В приведенной ниже таблице указаны расстояния между центрами распределения и продавцами, а также величины, характеризующие ежемесячный спрос и объемы поставок, исчисляемые количеством автомобилей:
| Центр распределения | Продавцы | Объем поставок, шт. | ||||
| Спрос на автомобили, шт. |
Определите минимальные затраты на доставку автомобилей.
Задание 2. Модели линейного программирования.
Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Сырьем для изготовления тканей являются пряжа и красители. Основные параметры производства, его себестоимость и цены реализации готового продукта показаны в таблице. Составить план производства тканей, обеспечивающий максимальную прибыль.
| Вид ресурса | Обьем ресурсов | Производительность и норма расхода | ||
| Артикул 1 | Артикул 2 | Артикул 3 | ||
| Станки 1 типа | 29000 часов | 20 м/час. | 10 м/час | 25 м/час |
| Станки 2 типа | 30000 часов | 8 м/час | 20 м/час | 10 м/час |
| Пряжа (кг) | 30000кг | 0.12 кг/м | 0.18 кг/м | 0.21 кг/м |
| Красители (кг) | 3000 кг | 0.01 кг/м | 0.005 кг/м | 0.008 кг/м |
| Цена 1 м ткани (руб.) | ||||
| Себестоимость 1 м ткани (руб) |
Вариант 12 и 27
Задание 1. Транспортная задача.
ДЦС должен отправить вагоны с четырех станций в шесть подъездных путей. На станциях имеется 30, 45, 25 и 20 вагонов, а для шести подъездных путей требуется соответственно 30, 20, 10, 40, 10 и 10 вагонов. Стоимость перевозки одного вагона со станции на подъездной путь приведена в таблице. Со станции № 3 на подъездной путь № 6 вагоны не отправляются
| Склады | Магазины | |||||
| - | ||||||
Разработайте план перевозок из условия минимизации расходов на транспортировку
Задание 2. Модели линейного программирования.
Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый (месячный) ассортимент и трудоемкость единицы продукции приведены в таблице. Запас древесностружечных плит, досок еловых и березовых 90, 30 и 14 м3 соответственно. Плановый фонд рабочего времени 16800 человеко-часов.
| Показатели | Трельяжи | Трюмо | Тумбочки |
| Норма расхода материала, м3 | |||
| древесностружечные плиты. | 0,032 | 0,031 | 0,038 |
| доски: еловые. | 0,020 | 0,020 | 0,006 |
| березовые..... | 0,005 | 0,005 | 0,006 |
| Трудоемкость, чел.-ч..... | 10,2 | 7,5 | 5,8 |
| Плановая себестоимость, руб. | 88,81 | 63,98 | 29,60 |
| Оптовая цена предприятия, руб. | 93,00 | 67,00 | 30,00 |
| Плановый ассортимент, шт. |
Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (или даже всем) показателям построить модель, на основе которой можно получить план производства мебели, максимизирующий прибыль.
Вариант 13 и 28
Задание 1. Транспортная задача.
Три завода A 1 , A 2 и A 3поставляют товар трем потребителям. Стоимость перевозки и объемы производства приведены в таблице:
| Заводы | Потребители | Объем производства, шт. | ||
| A1 | ||||
| A2 | ||||
| A3 | ||||
| Потребность, шт. |
Составьте оптимальный план перевозки.
Задание 2. Модели линейного программирования.
Фабрика выпускает кожаные брюки, куртки и пальто специального назначения в ассортименте, заданном отношением 2:1:3. В процессе изготовления изделия проходят три производственных участка – дубильный, раскройный и пошивочный. Фабрика имеет практически неограниченную сырьевую базу, однако сложная технология предъявляет высокие требования к квалификации рабочих. Численность их в рамках планируемого периода ограничена.
Время обработки изделий на каждом участке, их плановая себестоимость, оптовая цена предприятия приведены в таблице.
| Показатели | Брюки | Куртки | Пальто |
| Норма времени на участках, чел.-ч. | |||
| дубильном | 0,3 | 0,4 | 0,6 |
| раскройном | 0,4 | 0,4 | 0,7 |
| пошивочном | 0,5 | 0,4 | 0,8 |
| Полная себестоимость, руб. | 40,5 | 97,8 | |
| Оптовая цена предприятия, руб | 17,5 |
Ограничения на фонд времени для дубильного, раскройного, и пошивочного участков составляют соответственно 3360, 2688 и 5040 ч.
Учитывая заданный ассортимент, построить модель, на основе которой определить план производства одежды, максимизирующий прибыль от реализованной продукции.
Вариант 14 и 29
Задание 1. Транспортная задача.
В трех пунктах отправления A, B, C сосредоточен однородный товар. Этот товар необходимо перевезти в четыре пункта назначения P, Q, R, S. Запасы товара в пунктах отправления и потребности пунктов назначения показаны в таблице.
| Запасы (тонн) | Потребности (тонн) | |||||
| A | B | C | P | Q | R | S |
Стоимости в рублях перевозок 1 тонны груза из i-го пункта отправления в j-й пункт назначения заданы матрицей.
| A | B | C | |
| P | |||
| Q | |||
| R | |||
| S |
1) Найти план перевозок груза, обеспечивающий транспортному предприятию минимальную стоимость перевозок.
2) Как изменится решение задачи, если потребность в товаре в пункте Q уменьшится до 20 тонн?
Задание 2. Модели линейного программирования.
На приобретение оборудования для нового производственного участка выделено 300 д. ед. Его предполагается разместить на площади 45 кв. м. Участок может быть оснащен оборудованием трех видов – машинами стоимостью 6 тыс. руб. (здесь и далее все показатели приводятся на единицу оборудования), размещающимися на площади 9 кв. м, производительностью 8 тыс. единиц продукции за смену; машинами стоимостью 3 тыс. руб., занимающими площадь 4 кв. м, производительностью 4 тыс. единиц продукции за смену; машинами стоимостью 2 д. ед. Занимаемая ими площадь 3 кв. м, производительность 3 тыс. единиц продукции.
Построить модель, на основе которой определить план приобретения оборудования, обеспечивающий наибольшую производительность всего участка.
Вариант 15 и 30
Задание 1. Транспортная задача.
Четыре подъездных пути каждый день обеспечивают вагонами три станции. Станции подали заявки соответственно на 23, 15 и 42 вагона. Подъездные пути имеют с