Лабораторная работа № 3. ПОСТРОЕНИЕ ЛИНЕЙНОЙ МОДЕЛИ

1. Построить и провести анализ нелинейной логарифмической функции .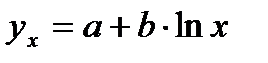

1.1. Для удобства производимых вычислений составить табл. 2.1, на основе исходных данных к работе (см. таб. 1.1).

Таблица 2.1

№										,%
…
Сумма
Среднее значение

Примечание: столбцы 8, 9, 10 заполняются после выполнения п.1.2, столбец 11 после п. 1.3.

1.2. Построить нелинейное логарифмическое уравнение парной регрессии 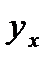от вида (2.1), найдя его параметры 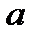и из выражений (2.5), предварительно сделав замену (2.2).

1.3. Рассчитать индекс корреляции (2.11), индекс детерминации (2.12) и ошибку аппроксимации (1.6).

1.4. Оценить статистическую значимость полученного уравнения регрессии в целом на основе F -критерия Фишера. Необходимо рассчитать фактическое значение F - критерия (2.13) и сравнить его с табличным значением (см. прил. 1).

1.5. Построить на графике исходные данные (зависимость y от x) и теоретическую кривую (рассчитанную по модели 2.1).

2. Аналогично с п. 1 построить и провезти анализ нелинейной функции с квадратным корнем вида , при этом для удобства проводимых вычислений составить табл. 2.1.

3. Аналогично с п. 1 построить и провести анализ нелинейной степенной функции , при этом для удобства проводимых вычислений составить табл. 2.2 (см. теоретические сведения).

Таблица 2.2

№									, %
…
Сумма
Среднее значение

 

4. Сравнить построенные в п. 1, п. 2, п. 3 модели по индексу детерминации и средней ошибки аппроксимации, составив табл. 2.3.

 

Таблица 2.3

Модель	Индекс детерминации	Средняя ошибка аппроксимации, ,%

 

Лабораторная работа № 3

ПОСТРОЕНИЕ ЛИНЕЙНОЙ МОДЕЛИ

МНОЖЕСТВЕННОЙ РЕГРЕССИИ

Цель работы: на основе исходных данных построить линейную модель множественной регрессии.

 

Теоретическая часть

 

Линейная модель множественной регрессии имеет вид

(3.1)

где – зависимая переменная (результативный признак); , , …, – независимые переменные (признак факторы).

Уравнение (3.1) позволяет по заданным значениям факторов , , …, находить теоретические значения результативного признака 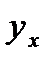, подставляя в него фактическое значение факторов , , …, .

Построение линейной модели множественной регрессии сводиться к оценке ее параметров – , , …, 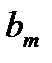. Для оценивания параметров линейной множественной регрессии применяется метод наименьших квадратов (МНК). Согласно данному методу параметры , , …, 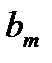находятся из решения систем линейных уравнений

(3.2)

 

где n – число наблюдений.

Двухфакторная модель линейной множественной регрессии (3.1) имеет вид

(3.3)

Система уравнений для оценивания параметров двухфакторной модели (3.3) построения на основе МНК согласно (3.2) будет иметь вид

(3.4)

Решая систему уравнений (3.4) относительно параметров , , и получим

(3.5)

 

где ,

Линейное уравнение множественной регрессии в стандартизированном масштабе будет иметь вид

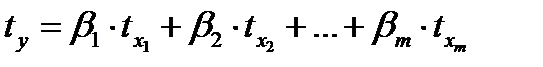(3.6)

где , , , 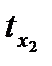…, – стандартизированные переменные , , для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ; - стандарти-зированные коэффициенты регрессии.

Двухфакторная модель линейной множественной регрессии в стандартизированном масштабе (3.6) имеет вид

. (3.7)

Метод наименьших квадратов также справедлив для нахождения стандартизированных коэффициентов регрессии. Эти коэффициенты показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов.

Коэффициенты «чистой» регрессии связаны со стандартизированными коэффициентами регрессии следующим соотношением

(3.8)

Используя соотношение (3.8), можно переходить от уравнения регрессии в стандартизированном масштабе (3.7) к уравнению регрессии в натуральном масштабе переменных (3.1), при этом параметр а определяется как

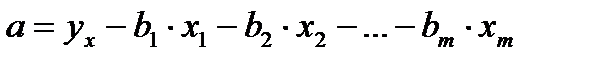. (3.9)

Частные коэффициенты эластичности определяются из выражения

(3.10)

где - коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии, которые связывает результативный признак с соответствующем фактором при закреплении остальных факторов на среднем уровне.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности коэффициенты эластичности

, (3.11)

которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%.

 

Практическая часть

Задание к работе

1. На основе исходных данных (см. таб. 3.1), где N – номер варианта, соответствующий трем последним цифрам номера зачетной книжки, построить и провести анализ двухфакторной линейной модели множественной регрессии от и .

2. Выписать пояснения к каждому выполненному пункту задания.

3. Сделать итоговый вывод об обоснованных результатах, полученных в ходе выполнения работы.

Таблица 3.1

Исходные данные для лабораторных работ №3 и №4

Номер измерения
	2,2 N	7,3 N	3,9 N
	3,1 N	9,1 N	8,1 N
	4,3 N	10,8 N	10,8 N
	5,3 N	12,9 N	13,3 N
	6,7 N	15,0 N	15,6 N
	7,4 N	16,6 N	19,5 N
	8,5 N	18,7 N	22,7 N
	9,1 N	20,2 N	24,8 N
	10,0 N	21,8 N	28,1 N
	11,2 N	24,1 N	30,4 N