1. Построение аддитивной модели временного ряда.
1.1. Провести выравнивание исходных данных ряда методом скользящей средней. Расчет оформить в виде таблицы (см. таб. 6.1).
1.1.1. Просуммировать уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени (столбец 3 табл. 6.1).
1.1.2. Разделив полученные суммы на 4, найти скользящие средние (столбец 4 табл. 6.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.1.3. Найти центрированные скользящие средние, приведя скользящие среднее значение в соответствии с фактическими моментами времени. Для этого необходимо найти среднее значение из двух последовательных скользящих средних (столбец 5 табл. 6.1).
1.1.4. Найти оценки сезонной компоненты (столбец 6 табл. 6.1) как разность между фактическими уровнями ряда (столбец 2 табл. 6.1) и центрированными скользящими средними (столбец 5 табл. 6.1).
Таблица 6.1
| t | y | Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| - | - | - | - | |
| 
| 
| - | - | |
| 
| 
| 
| 
| |
| 
| 
| 
| 
| |
| 
| 
| 
| 
| |
| … | … | … | … | … | … |
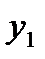
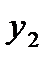
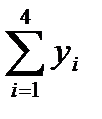
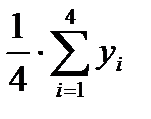
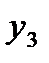
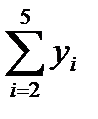
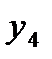
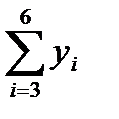
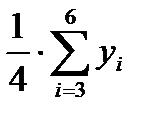
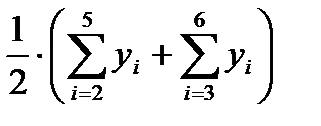
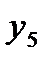
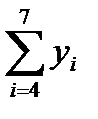
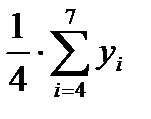
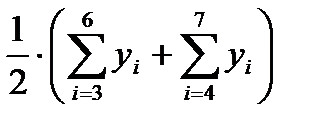
1.2. Используя оценки сезонной компоненты (столбец 6 табл. 6.1) рассчитать значения сезонной компоненты S. Расчет оформить в виде таблицы (см. табл. 6.2).
1.2.1. Найти средние за каждый квартал (по всем годам) оценки сезонной компоненты 
.
1.2.2. Найти корректирующий коэффициент k, используя следующее выражение
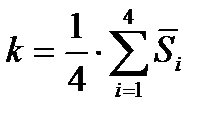(6.3)
1.2.3. Рассчитать скорректированные значения сезонной компоненты 
, используя выражение
(6.4)
1.2.4. В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. Поэтому необходимо проверить равенство нулю суммы значений сезонной компоненты и прокомментировать полученный результат.
Таблица 6.2
| Показатели | Год | № квартала | |||
| Оценка сезонной компоненты | |||||
| Всего за i -й квартал | |||||
Средняя оценка сезонной компоненты для i - го квартала,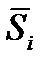 
| |||||
| Скорректированная сезонная компонента,
|
1.3. Исключить влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного времени ряда (столбец 4 табл. 6.3). Полученные значения рассчитываются за каждый момент времени и содержат только трендовую T и случайную компоненту Е временного ряда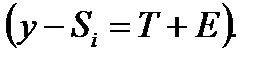 
1.4. Определить трендовую компоненту T данной модели (столбец 5 табл. 6.3). Уравнение линии тренда имеет вид
(6.5)
где t – номер квартала.
Модель (6.5) фактически представляет собой линейное уравнение парной регрессии. Для нахождения параметры a и b данной модели используется МНК (см. лабораторную работу №1). Подставляя в полученное уравнение (6.5) значения t = 1, 2,…, 16, найти уровни T для каждого момента времени t, (столбец 5 табл. 6.3).
Таблица 6.3
| t | y |
|  
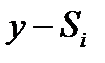
| T | T+S | 
| 
|
| … |
1.5. Найти значения уровней ряда, полученные по аддитивной модели. Для этого необходимо прибавить к уровням трендовой компоненты T значения сезонной компоненты S для каждого квартала (столбец 6 табл. 6.3).
1.6. На одних координатных осях построить графики зависимости фактических значений уровней временного ряда y (столбец 2 табл. 6.3) и теоретических T+S (столбец 6 табл. 6.3) от соответствующих кварталов t (столбец 1 табл. 6.3).
1.7. Оценить и прокомментировать качество построенной модели на основе коэффициента детерминации
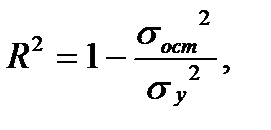(6.6)
где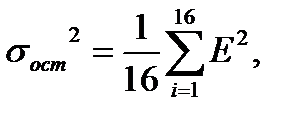 
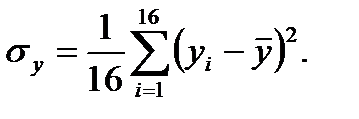
1.8. Сделать прогноз на следующие два квартала (t = 17; 18) по построенной аддитивной модели. Прогнозное значение F уровня временного ряда в аддитивной модели есть сумма трендовой T и сезонной компонент S
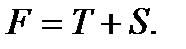(6.7)
1.8.1. Определить трендовые компоненты T (17) и T (18) на основе модели тренда (6.5).
1.8.2. Выбрать для из табл. 6.3 значения сезонных компонент для соответствующих кварталов.
1.8.3. Согласно выражению (6.7) найти прогнозное значения уровней временного ряда F (17), F (18).
2. Построение мультипликативной модели временного ряда
2.1. Провести выравнивание исходных данных ряда методом скользящей средней.
2.1.1. Просуммировать уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени (столбец 3 табл. 6.4).
2.1.2. Разделив полученные суммы на 4, найти скользящие средние (столбец 4 табл.6.4).
2.1.3. Найти центрированные скользящие средние. Для этого необходимо найти средние значения из двух последовательных скользящих средних (столбец 5 табл.6.4).
Таблица 6.4
| t | y | Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка компоненты |
| - | - | - | - | |
| 
| 
| - | - | |
| 
| 
| 
| 
| |
| 
| 
| 
| 
| |
| 
| 
| 
| 
| |
| … | … | … | … | … | … |
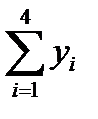
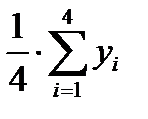
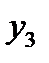
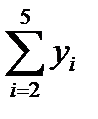
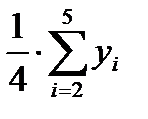
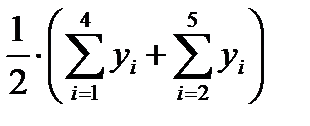
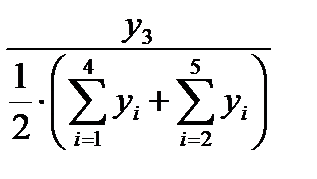
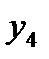
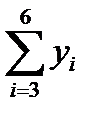
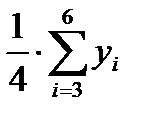
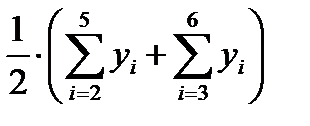
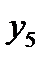
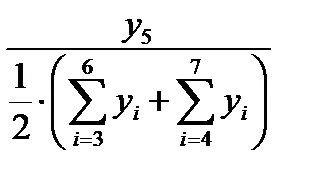
2.1.4. Найти оценки сезонной компоненты как частное от деления фактических уровней ряда (столбец 2 табл. 6.4) на центрированные скользящие средние (столбец 5 табл. 6.4).
2.2. Используя оценки сезонной компоненты (столбец 6 табл. 6.4) рассчитать значения сезонной компоненты S. Расчет оформить в виде табл. 6.5.
2.2.1. Найти средние за каждый квартал (по всем годам) оценки сезонной компоненты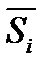 
.
2.2.2. Найти корректирующий коэффициент k, используя следующее выражение
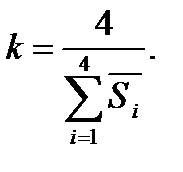(6.8)
2.2.3. Рассчитать скорректированные значения сезонной компоненты , используя выражение
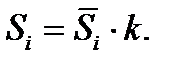(6.9)
Таблица 6.5
| Показатели | Год | № квартала | |||
| Оценка сезонной компоненты | |||||
| Всего за i -й квартал | |||||
| Средняя оценка сезонной компоненты для i - го квартала,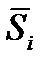
| |||||
| Скорректированная сезонная компонента,
|
2.2.4. В мультипликативных, как и в аддитивных моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В данном случае число периодов одного цикла ровно четыре. Поэтому необходимо проверить равенство четырем суммы значений сезонной компоненты и прокомментировать полученный результат.
2.3. Исключить влияние сезонной компоненты, деля на ее значение каждый уровень исходного временного ряда (столбец 4 табл. 6.6). Полученные значения рассчитываются за каждый момент времени и содержат только трендовую T и случайную компоненту Е временного ряда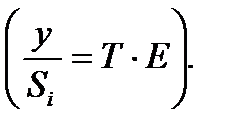 
Таблица 6.6
| t | y |
| 
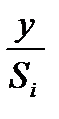
| T | T  S
| 
|
| … |
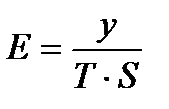
2.4. Определить трендовую компоненту T данной модели (столбец 5 табл. 6.6). Уравнение линии тренда имеет вид
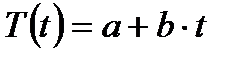(6.10)
где t – номер квартала.
Модель (6.10) фактически представляет собой линейное уравнение парной регрессии. Для нахождения параметры a и b данной модели используются МНК (см. лабораторную работу №1). Подставляя в полученное уравнение значения t = 1, 2, …, 16, найти уровни T для каждого момента времени t (столбец 5 табл. 6.6).
2.5. Найти значения уровней ряда, умножив уровни трендовой компоненты T на соответствующие сезонной компоненты S для каждого квартала (столбец 6 табл. 6.6).
2.6. На одних координатных осях построить графики зависимости фактических значений уровней временного ряда y (столбец 2 табл. 6.6) и теоретических T 
S (столбец 6 табл. 6.6) от соответствующих кварталов t (столбец 1 табл. 6.6).
2.7. Оценить и прокомментировать качество построенной модели на основе коэффициента детерминации
(6.11)
где 
2.8. Сделать прогноз на следующие два квартала (t = 17; 18) по построенной мультипликативной модели. Прогнозное значение F уровня временного ряда в мультипликативной модели есть произведение трендовой T и сезонной компонент S
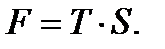(6.12)
2.8.1. Определить трендовые компоненты T (17) и T (18) на основе модели тренда (6.10).
2.8.2. Выбрать из табл. 6.6 значения сезонных компонент для соответствующих кварталов.
2.8.3. Согласно выражению (6.12) найти прогнозное значения уровней временного ряда F (17), F (18).
Приложение 1.
Значение F - критерия Фишера при уровне значимости 
| 
| |||||||||
| 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 233,9 | 238,9 | 243,9 | 249,0 | 254,3 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 4,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 3,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
Приложение 2.
Критические значения t - критерия Стьюдента
при уровне значимости 0,10; 0,05; 0,01 (двухсторонний)
| Число степеней свободы d.f. | 
| Число степеней свободы d.f |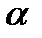 
| ||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | ||
| 6,3138 | 12,706 | 63,657 | 1,7341 | 2,1009 | 2,8784 | ||
| 2,9200 | 4,3027 | 9,9248 | 1,7291 | 2,0930 | 2,8609 | ||
| 2,3534 | 3,1825 | 5,8409 | 1,7247 | 2,0860 | 2,8453 | ||
| 2,1318 | 2,7764 | 4,5041 | 1,7207 | 2,0796 | 2,8314 | ||
| 2,0150 | 2,5706 | 4,0321 | 1,7171 | 2,0739 | 2,8188 | ||
| 1,9432 | 2,4469 | 3,7074 | 1,7139 | 2,0687 | 2,8073 | ||
| 1,8946 | 2,3646 | 3,4995 | 1,7109 | 2,0639 | 2,7969 | ||
| 1,8595 | 2,3060 | 3,3554 | 1,7081 | 2,0595 | 2,7874 | ||
| 1,8331 | 2,2622 | 3,2498 | 1,7056 | 2,0555 | 2,7787 | ||
| 1,8125 | 2,2281 | 3,1693 | 1,7033 | 2,0518 | 2,7707 | ||
| 1,7959 | 2,2010 | 3,1058 | 1,7011 | 2,484 | 2,7633 | ||
| 1,7823 | 2,1788 | 3,0545 | 1,6991 | 2,0452 | 2,7564 | ||
| 1,7709 | 2,1604 | 3,0123 | 1,6973 | 2,0423 | 2,7500 | ||
| 1,7613 | 2,1448 | 2,9768 | 1,6839 | 2,0211 | 2,7045 | ||
| 1,7530 | 2,1315 | 2,9467 | 1,6707 | 2,0003 | 2,6603 | ||
| 1,7459 | 2,1199 | 2,9208 | 1,6577 | 1,9799 | 2,6174 | ||
| 1,7396 | 2,1098 | 2,8982 | 
| 1,6449 | 1,9600 | 2,5758 |
.
Библиографический список
Основная литература
1. Бывшев, В.А. Эконометрика [Текст]: учеб. пособие / В. А. Бывшев. – М.: Финансы и статистика, 2008. – 480 с.
2. Глухов, Д.А. Эконометрика [Текст]: учеб. пособие / Д.А. Глухов; М-во образования и науки РФ, ФГБОУ ВПО «ВГЛТА». – Воронеж, 2013. – 116 с.
Дополнительная литература
3. Гладилин, А.В. Эконометрика [Текст]: учеб. пособие / А. В. Гладилин, А.Н. Герасимов, Е.И. Громов. – 2-е изд., стер. – М.: КНОРУС, 2009. – 231 с.
4. Просветов, Г.И. Эконометрика: задачи и решения [Текст]: учеб.-практ. пособие / Г.И. Просветов. – 5-6 изд., доп. – М.: Альфа-Пресс, 2008. – 192 с.
Светлана Вячеславовна Писарева
ЭКОНОМЕТРИКА
Методические указания к лабораторным работам
для студентов по направлению подготовки
38.03.01 – Экономика
Редактор Е.А. Богданова
Подписано в печать 23.09.2014. Формат 60×90 /16.
Усл. печ. л. 3,5. Уч.-изд. л. 3,93. Тираж 50 экз. Заказ
ФГБОУ ВО «Воронежский государственный лесотехнический университет имени Г.Ф. Морозова»
РИО ФГБОУ ВО «ВГЛТУ». 394087, г. Воронеж, ул. Тимирязева, 8
Отпечатано в УОП ФГБОУ ВО «ВГЛТУ»
394087, г. Воронеж, ул. Докучаева, 10