9.1. ЛИТЕЙНЫЕ РАДИУСЫ, РАДИУСЫПЕРЕХОДОВ И
СОПРЯЖЕНИЙ СТЕНОК ЛИТЫХ ИЗДЕЛИЙ
Литейный радиус предусматривается в углах стенок отливки. Слишком малый литейный радиус приводит к подрыву формы (стержня), отбелу кромок и появлению холодных трещин в чугунных отливках.
Величина литейного радиуса выбирается в зависимости от толщины стенки отливки.
В реальных отливках на литейный радиус кроме толщины стенки влияют склонность к подрыву и трещинам песчано-глинистых форм и стержней при их выеме и склонность к образованию отбела и холодных трещин в чугунных отливках.
Требования для неуказанных литейных радиусов указываются на чертеже отливки надписью типа: «Неуказанные литейные радиусы R 3 мм».
Литейный радиус (R = 0) отсутствует в плоскости разъема и на пересечении формы и стержня, так как в этих местах, как правило, образуются заливы, которые впоследствии зачищаются.
Малый радиус приводит к напряжениям и как следствие к трещинам в отливках, большой — к увеличению массы отливки, усадочным дефектам в отливках (увеличению теплового узла).
Плавность перехода от тонких к толстым сечениям, правильное сопряжение и достаточная величина радиусов обеспечивают получение отливок без литейных дефектов (усадочных раковин, пористости, трещин и т.д.). В правильно сконструированной литой детали отношение толщин стенок (h) должно удовлетворять неравенству h1/h2≤ 2. В машиностроительных отливках приведенное отношение может быть больше — h1/h2≤ 4.
Сопряжения стенок, различающихся по толщине менее чем в 2 раза, выполняются посредством радиуса перехода Rп или радиуса сопряжения Rc (рис. 9.1, а, б, в). Радиус сопряжения Rc. можно определить по уравнению
Rc =К(h1+ h2)/2,
Где: К=1/2 …1/3
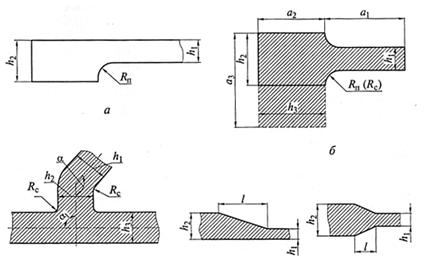
Рис. 9.1. Радиусы R односторонних (а) и двусторонних (б) переходов, радиусы R сопряжений (в), длина L сопряжений стенок в виде клина (г): h1, h2, h3 — толщины стенок; а1, а2,а3 — протяженность стенки; α — угол сопряжения
Радиус угловых L-образных сопряжений (Rc) зависит не только от толщины стенки, но и от угла α между сопрягаемыми стенками (рис. 9.1, в.
Таблица 9.1
Радиусы сопряжений Rc стенок отливки
| (h1+h2)/2, мм | Величина Rc, мм, в зависимости от угла сопряжения α, | |||||
| до 50 | свыше 50÷75 | свыше 75÷105 | свыше 105÷135 | свыше 135÷165 | свыше 165 | |
| До 1,5 | 0,6 | 1,0 | 1,2 | 1,5 | 2,0 | 2,5 |
| Свыше 1,5 до 3 | 0,8 | 1,2 | 1,5 | 2,0 | 2,5 | 3,0 |
| Свыше 3 до 5 | 2,5 | 3,0 | 4,0 | 4,0 | 5,0 | 6,0 |
| Свыше 5 до 8 | 3,0 | 4,0 | 5,0 | 5,0 | 6,0 | 8,0 |
| Свыше 8 до 10 | 4,0 | 5,0 | 6,0 | 6,0 | 8,0 | 10,0 |
| Свыше 10 до 20 | 5,0 | 6,0 | 8,0 | 8,0 | 10,0 | 12,0 |
| Свыше 20 до 30 | 6,0 | 8,0 | 10,0 | 10,0 | 12,0 | 14,0 |
| Свыше 30 до 40 | 8,0 | 10,0 | 12,0 | 12,0 | 14,0 | 16,0 |
| Свыше 40 до 50 | 10,0 | 12,0 | 14,0 | 14,0 | 16,0 | 18,0 |
| Свыше 50 | 12,0 | 14,0 | 16,0 | 16,0 | 18,0 |
Следует также различать радиусы сопряжений Rc и радиусы переходов Rп.
Из рис. 9.1, б видно, что при определении радиуса сопряжения Rc или перехода Rп возможна некоторая неопределенность. Действительно, если радиус определяется для сплошного контура, то принимают во внимание толщины стенок h1 и h2, если же учесть показанный на рисунке штрихом контур, то во внимание принимаются толщины стенок h1 и h2. Для устранения неопределенности при нахождении Rп и Rc следует учесть протяженность стенок.
На основании практического опыта принято граничное значение протяженности [аi], которое для первой и второй стенок составляет
[а]1 = (h1/2) + 7;
[а]2 = (h2/2) + 7.
Реальную протяженность стенки по чертежу следует сравнить с граничным значением, вычисленным для каждой из стенок по приведенным уравнениям, и выбрать вид радиуса.
Если а1 > [а]1 и а2 > [а2], то определяется Rc;
для трех пар неравенств - а1 ≤ [а]1 и а2 ≤ [а]2, а1 ≤ [а]1 и а2 ≥ [а]2, а1 ≥ [а]1 и а2 ≤ [а]2
определяется Rп
Радиусы переходов односторонних (рис. 9.1, а) и двусторонних (рис. 9.1, б) определяются по таблице 9.2. при прочих равных условиях радиусы сопряжения и переходов для отливок из алюминиевых сплавов в 1,25 раза меньше, а для стальных в 1,25 раза больше, чем для чугунных.
Если отношение толщин сопрягаемых стенок более 2, то переход двух стенок выполняют в виде клина (рис. 9.1, г).
Длина клина L рассчитывается по уравнению
L = 4(h1 - h2).
Радиусы сопряжения и переходов назначаются при конструировании литой детали. Однако этот параметр является оценочным с точки зрения технологичности, но его также назначает технолог после нанесения припусков на сопрягаемые поверхности и технологических напусков.
Таблица 9.2. Радиусы переходов Rп
| (h1+h2)/2, мм | 5< | 5-6 | 6-8 | 8-10 | 10-12 | 12-14 | 14-18 | 18-20 | До 25 | |
| Величина Rп, мм, переходов | односторонних | |||||||||
| двусторонних |