Для уменьшения износа профиля кулачка и потерь на трение толкатель снабжают роликом. Размер ролика r выбирают из условия выполнения закона движения (чтобы не получить заострение практического профиля кулачка): 
– и из условия конструктивности: 
где 
– минимальный радиус профиля кулачка; 
– минимальный радиус кривизны профиля кулачка на выпуклой части.
Участки теоретического профиля кулачка с наименьшим 
определяют визуально. Затем для этих участков (или одного участка на рис. 6.11) находят центр среднего круга кривизны, проходящего через три близлежащие точки. Средний круг кривизны можно определить и с помощью хорд, соединяющих соседние точки со средней точкой. Через середины каждой из хорд проводят перпендикуляры и находят их пересечение. В точке их пересечения будет находиться центр кривизны. Окончательно радиус ролика берется меньший из двух вычисленных по формулам:
Для вычерчивания практического профиля нужно провести ряд окружностей радиусом ролика с центрами на теоретическом профиле, и огибающая этих окружностей будет практическим профилем кулачка.
6.7. Определение минимальных размеров
кулачка с коромыслом
Для решения этой задачи задаются: закон движения, минимальный угол передачи движения 
, циклограмма или фазовые углы, длина коромысла l и максимальный угол качания коромысла 
.
Порядок расчета напоминает порядок расчета минимальных размеров кулачка с поступательно движущимся толкателем.
Вначале строят графики перемещения, первой и второй производной перемещения по углу поворота кулачка. Перемещение можно выразить в угловых единицах или в линейных, закон движения при этом не изменится, так как 
, где l – длина коромысла, величина постоянная; 
– угол качания коромысла, рад; 
– максимальный дуговой путь конца коромысла.
Графики перемещения и первой производной перемещения по углу поворота кулачка строят в одинаковых масштабах. Метод построения остается прежним.
Строят совмещенный график. Для этого из произвольно взятой точки С (рис. 6.12) радиусом 
(
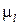– масштаб для определения параметров кулачка) проводят дугу 
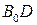и соединяют точку 
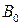с точкой С.
Далее от точки B 0 по этой дуге откладывают с графика перемещения соответствующие отрезки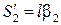 
, где l – длина коромысла, β – угол качания коромысла.
Полученные точки B 0; 2; 3; 4 и т.д. представляют положения центра коромысла, соответствующие заданным углам поворота кулачка.
Рис. 6.12. Совмещенный график перемещения
кулачка с коромыслом
Для определения центра O 1 вращения кулачка необходимо на лучах CB 0, CB 1, CB 2 и т.д. отложить отрезки 
в масштабе 
. При этом следует придерживаться следующего правила: при вращении кулачка и коромысла в одном направлении на фазе удаления отрезки 
откладываются по соответствующим лучам от дуги радиусом B 0 C в направлении C, а отрезки 
на фазе сближения – в сторону, противоположную точке С. При вращении кулачка и коромысла в противоположных направлениях (см. рис. 6.12) отрезки откладываются от дуги радиусом B 0 C в сторону, противоположную центру С вращения коромысла, а отрезки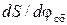 
– в сторону точки С.
В результате получают точки B 0, B 1 и т.д. Через эти точки проводят прямые под углом γmin к соответствующим лучам. Область, ограниченная этими прямыми (на рис. 6.12 она заштрихована), может рассматриваться как поле возможных центров вращения кулачка. Причем для любой точки поля будет выполняться условие, что во время работы кулачка угол передачи γ на всех фазах не будет меньше γmin. На рис. 6.12 за центр вращения кулачка взята точка O 1. Расстояние O 1 B 0 дает величину в масштабе 
. Расстояние aw = O 1 C называется межосевым R min.
Построение профиля кулачка показано на рис. 6.13. Из произвольной точки O 1 проводят окружность радиусом O 1 C 0. Масштаб построения профиля может быть сохранен или взят другим, тогда новый масштаб
¨ где 
– осевое расстояние (истинное), определяемое согласно рис. 6.12; O 1 С 0 – отрезок, изображающий осевое расстояние в новом масштабе 
построения профиля (см. рис. 6.13).
На этой окружности от точки C 0 в сторону, противоположную вращению кулачка, откладывают фазовые углы, которые, в свою очередь, делят на соответствующее число равных частей, как и на графике перемещения. На рис. 6.13 деление нанесено через одно 0, 2, 4 и т.д. Из точки O 1 радиусом R min проводят окружность, а из точки C 0 радиусом, равным длине коромысла B 0 C 0 – дугу, на которой откладывают дуговой путь согласно графику перемещений. Полученные точки дают положения коромысла при повороте кулачка на соответствующий угол. Из точки O 1 как из центра проводят окружности через точки деления дуги B 0 D . Из точек C 1; C 2 и т.д. циркулем делают засечки на соответствующих окружностях
Рис. 6.13. Построение профиля кулачка с коромыслом
радиусом B 0 C 0. Полученные таким образом точки принадлежат центровому профилю кулачка. Соединив их плавной кривой, получают центровой профиль.
Радиус ролика и конструктивный (практический) профиль кулачка определяется так же, как и для кулачкового механизма с поступательно движущимся толкателем.
6.8. Определение минимальных размеров кулачка
с плоским толкателем