 Рис. 6.18. Расчетная схема для кинематического анализа
Рис. 6.18. Расчетная схема для кинематического анализа
| Этот анализ проведем на примере кулачкового механизма с толкателем, оканчивающимся острием.
Пусть на фазе удаления центровой профиль кулачка задан в виде канонического уравнения параболы у = 2 рх в системе координат х О у (рис. 6.18).
На рис. 6.18 использованы следующие обозначения:
а – расстояние от начала координат до центра окружности минимального радиуса;
φ – текущий фазовый угол поворота кулачка;
 – координаты точки М профиля кулачка при повороте последнего на угол φ; – координаты точки М профиля кулачка при повороте последнего на угол φ;
|
 – координаты точки
– координаты точки  встречи толкателя с точкой на профиле кулачка;
встречи толкателя с точкой на профиле кулачка;
 – соответственно эксцентриситет и минимальный радиус кулачка;
– соответственно эксцентриситет и минимальный радиус кулачка;
 ,
,  ,
,  m, n,
m, n,  – точки построения схемы механизма.
– точки построения схемы механизма.
В дальнейшем будем считать заданными:
1) уравнение центрового профиля кулачка;
2) расстояние а;
3) эксцентриситет е;
4) угловую скорость ω;
5) текущий фазовый угол.
Требуется определить координаты  точки встречи толкателя
точки встречи толкателя
с точкой профиля кулачка при повороте последнего на угол φ, а также скорость в данный момент.
Определим минимальный радиус. Из рис. 6.18 следует:
 , (6.4)
, (6.4)
 , (6.5)
, (6.5)
x = а – е. (6.6)
¨ Подставляя в формулу (6.4) значения (6.5), (6.6), получим
 (6.7)
(6.7)
 Определим на профиле кулачка координаты точки М, которая окажется в контакте с толкателем при повороте кулачка на заданный фазовый угол φ. Для этого необходимо совместно решить уравнение профиля кулачка и уравнение прямой у = kx + b, изображающей положение толкателя в обращенном движении (см. рис. 6.18).
Определим на профиле кулачка координаты точки М, которая окажется в контакте с толкателем при повороте кулачка на заданный фазовый угол φ. Для этого необходимо совместно решить уравнение профиля кулачка и уравнение прямой у = kx + b, изображающей положение толкателя в обращенном движении (см. рис. 6.18).
Составим уравнения упомянутой прямой в системе х О у. Угловой коэффициент этой прямой равен tg(90 – φ). Отрезок, отсекаемый на оси О у (с учетом знака) и равный О  , определяется из следующих условий (см. рис. 6.18):
, определяется из следующих условий (см. рис. 6.18):

 (6.8)
(6.8)
¨ отсюда
 (6.9)
(6.9)
Тогда уравнение искомой прямой с учетом углового коэффициента и выражения (6.9) примет следующий вид:
 (6.10)
(6.10)
Решаем совместно уравнение (6.10) и уравнение параболы:
 (6.11)
(6.11)
Решение системы уравнений (6.11) – это координаты точки М:
 (6.12)
(6.12)
Дифференцируя выражения (6.12) по времени, получим:
 (6.13)
(6.13)
Определим  координаты точки
координаты точки  встречи толкателя с точкой М на профиле кулачка. В соответствии с рис. 6.18 имеем:
встречи толкателя с точкой М на профиле кулачка. В соответствии с рис. 6.18 имеем:
 . (6.14)
. (6.14)
¨ Координату  определим из треугольника
определим из треугольника 
 :
:
 . (6.15)
. (6.15)
Радиус-вектор 
 =
=  M определим как расстояние между двумя точками М и
M определим как расстояние между двумя точками М и  , координаты которых известны (М (
, координаты которых известны (М ( ),
),  (a, 0)):
(a, 0)):
 (6.16)
(6.16)
¨ Подставляя выражения (6.16) в (6.15), получаем:
 (6.17)
(6.17)
Дифференцируя (6.17) по времени, получим абсолютную скорость толкателя при повороте кулачка на заданный угол:
 . (6.18)
. (6.18)
Производные  и
и  определяются по формулам (6.13). Дифференцируя по времени выражение (6.18), можно определить ускорение толкателя.
определяются по формулам (6.13). Дифференцируя по времени выражение (6.18), можно определить ускорение толкателя.
6.10.3. Профилирование кулачковой шайбы
для механизмов с плоским толкателем
Для управления станками с ЧПУ при изготовлении кулачковых шайб требуется аналитическое выражение центрового и действительного профилей. Предлагаемый аналитический метод профилирования кулачковых шайб механизмов различных типов позволяет формализовать процесс определения координат профиля в декартовой или полярной системе координат с помощью ЭВМ. Применим данный метод при профилировании кулачковой шайбы с плоским толкателем.
Рассмотрим неподвижную систему координат  и подвижную систему координат
и подвижную систему координат  , жестко связанную с шайбой (рис. 6.19). Перемещение системы
, жестко связанную с шайбой (рис. 6.19). Перемещение системы  относительно
относительно  характеризуется поворотом кулачка на угол φ, при φ = 0 оси систем координат совпадают.
характеризуется поворотом кулачка на угол φ, при φ = 0 оси систем координат совпадают.
В системе  координаты точки контакта
координаты точки контакта  определим радиусом-вектором
определим радиусом-вектором  которому соответствует столбцовая матрица:
которому соответствует столбцовая матрица:
 .
.
В системе  координаты точки контакта
координаты точки контакта  определим радиусом – вектором
определим радиусом – вектором  с помощью векторного выражения:
с помощью векторного выражения:
 ,
,
¨ где  – матрица перехода от системы
– матрица перехода от системы  к системе
к системе  ,
,

Рис. 6.19. Профилирование кулачковой шайбы
для механизма с плоским толкателем

Тогда, согласно определению вектора,
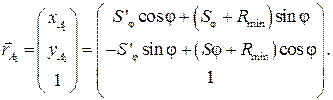
В полярных координатах радиус-вектор кулачка

а полярный угол  , где
, где  – угол, зависящий от координат точки
– угол, зависящий от координат точки  на профиле кулачка,
на профиле кулачка,  .
.
6.10.4. Профилирование кулачковой шайбы для механизмов
с толкателем, оканчивающимся острием или роликом
В неподвижной системе координат  радиус-вектор точки контакта
радиус-вектор точки контакта  толкателя с шайбой представим столбцовой матрицей (рис. 6.20):
толкателя с шайбой представим столбцовой матрицей (рис. 6.20):

¨ где  – положение толкателя в начале его подъема;
– положение толкателя в начале его подъема;
¨  – текущее перемещение толкателя.
– текущее перемещение толкателя.
В системе  координаты точки контакта
координаты точки контакта  определим радиусом-вектором,
определим радиусом-вектором,  с помощью матричного выражения:
с помощью матричного выражения:

¨ где  – матрица перехода от системы
– матрица перехода от системы  к системе
к системе  ,
,

Рис. 6.20. Профилирование шайбы для механизма
с толкателем, оканчивающимся острием
 ,
,
¨  – координаты радиуса-вектора
– координаты радиуса-вектора  .
.
Для перехода от центрового к практическому профилю запишем вектор  координат точки
координат точки  контакта ролика с действительным профилем кулачка в начале подъема толкателя в системе координат
контакта ролика с действительным профилем кулачка в начале подъема толкателя в системе координат  :
:

¨ где  – угол давления,
– угол давления, 
¨  – аналог скорости толкателя,
– аналог скорости толкателя, 
¨  – радиус ролика.
– радиус ролика.
Тогда радиус-вектор точки контакта ролика и практического профиля (точки  ) в матричном выражении в системе
) в матричном выражении в системе  запишем в виде столбцовой матрицы:
запишем в виде столбцовой матрицы:

Для перехода к полярным координатам введем следующие обозначения:
 – постоянный угол,
– постоянный угол,  ;
;
 – дополнительный угол,
– дополнительный угол,  .
.
Отсюда полярный угол радиуса-вектора  . В полярных координатах радиус-вектор кулачка:
. В полярных координатах радиус-вектор кулачка:

6.10.5. Профилирование кулачковой шайбы
для механизма с коромыслом
При профилировании считаем заданными зависимость  углового перемещения выходного звена ψ от угла поворота кулачка φ, а также первую и вторую производные этого перемещения (ψ́, ψ˝), длину коромысла
углового перемещения выходного звена ψ от угла поворота кулачка φ, а также первую и вторую производные этого перемещения (ψ́, ψ˝), длину коромысла  , межосевое расстояние
, межосевое расстояние  , минимальный радиус, радиус ролика
, минимальный радиус, радиус ролика  .
.
На рис. 6.21 изображены неподвижная система координат  и подвижная система координат
и подвижная система координат  , которые совпадают при φ = 0, при этом начальное положение коромысла характеризуется значением
, которые совпадают при φ = 0, при этом начальное положение коромысла характеризуется значением  . Повороту кулачка на угол φ соответствует текущее положение коромысла ψ.
. Повороту кулачка на угол φ соответствует текущее положение коромысла ψ.
В системе  координаты точки контакта
координаты точки контакта  определим радиусом-вектором
определим радиусом-вектором  , которому соответствует столбцовая матрица:
, которому соответствует столбцовая матрица:
 .
.

Рис. 6.21. Профилирование кулачковой шайбы
для механизма с коромыслом
В системе  координаты точки контакта
координаты точки контакта  определим матричным выражением
определим матричным выражением

где  – матрица перехода от системы
– матрица перехода от системы  к системе
к системе  ,
,
 .
.

В полярной системе координат радиус-вектор текущего положения точки контакта кулачка и толкателя  , а полярный
, а полярный  .
.
Для описания практического профиля проводим нормаль к профилю n – n и вводим еще одну систему координат  с центром в точке А. В этой системе радиус-вектор, описывающий практический профиль, представим в виде
с центром в точке А. В этой системе радиус-вектор, описывающий практический профиль, представим в виде
 ,
,
¨ где θ – угол давления,
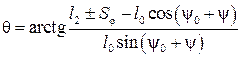 .
.
Для представления радиуса-вектора в системе  запишем матричное выражение:
запишем матричное выражение:

¨ где  ,
,  ,
,  – матрицы преобразования координат.
– матрицы преобразования координат.
Для примера рассмотрим составление матрицы для текущего положения толкателя:
 .
.
Координаты Х и Y начала координат А системы  в неподвижной системе
в неподвижной системе  (рис. 6.22) определим так:
(рис. 6.22) определим так:


Рис. 6.22. Определение столбца координат подвижной
системы координат в неподвижной системе координат
Из матричного выражения получаем матрицу, содержащую координаты практического профиля:
