§ 1. Синус, косинус и тангенс угла.
94.
○ Определение. Основным тригонометрическим тождеством называется равенство 
.
§ 2. Соотношения между сторонами и углами треугольника.
96.
n Теорема (о площади треугольника). Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
97.
n Теорема (синусов). Стороны треугольника пропорциональны синусам противолежащих углов.
○ Теорема (синусов, расширенная). Отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности.
98.
● Теорема (косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
§ 3. Скалярное произведение векторов.
101.
Определение. Два вектора называются перпендикулярными, если угол между ними равен 90°.
102.
n Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
○ Теорема. Скалярное произведение ненулевых векторов равно 0 тогда и только тогда, когда эти векторы перпендикулярны.
○ Определение. Скалярным квадратом вектора называется скалярное произведение вектора на себя и обозначается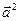 
.
○ Теорема. Скалярный квадрат вектора равен квадрату его длины: 
.
103.
n Теорема. Скалярное произведение векторов 
и 
выражается формулой: 
.
● Следствие 1 (условие перпендикулярности векторов). Ненулевые векторы 
и 
перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0 (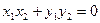
).
|
|
n Следствие 2 (косинус угла между векторами). Косинус угла между ненулевыми векторами 
и 
выражается формулой: 
.
104.
n Теорема (основные свойства скалярного произведения векторов). Для любых векторов 
, 
, 
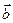и любого числа k справедливы соотношения:
1. 
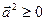, причем 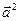>0 при 
;
2. 
(переместительный закон);
3. 
(распределительный закон);
4. 
(сочетательный закон).
ГЛАВА 12
Длина окружности и площадь круга.
§ 1. Правильные многоугольники.
105.
n Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
106.
n Теорема. Около любого правильного многоугольника можно описать окружность, и притом только одну.
107.
n Теорема. В любой правильный многоугольник можно вписать окружность, и притом только одну.
● Следствие 1. Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах.
● Следствие 2. Центр окружности, вписанной в правильный многоугольник, совпадает с центром окружности, описанной около него.
○ Определение. Центром правильного многоугольника называется центр окружности, вписанной в него или описанной около него.
108.
○ Теорема (площадь правильного многоугольника). Площадь правильного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
109.
○ Замечание. Не все правильные многоугольники можно построить с помощью циркуля и линейки.
§ 2. Длина окружности и площадь круга.
|
|
110.
○ Теорема. Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей.
○ Теорема. Длина окружности радиуса R выражается формулой: 
.
○ Теорема. Длина дуги окружности радиуса R выражается формулой: 
(α в градусах) или 
(α в радианах).
111.
○ Определение. Кругом называется часть плоскости, ограниченная окружностью.
○ Теорема. Площадь круга радиуса R выражается формулой: 
.
112.
n Определение. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
○ Определение. Дугой сектора называется дуга, которая ограничивает этот сектор.
○ Теорема. Площадь сектора радиуса R выражается формулой: 
(α в градусах) или 
(α в радианах).
ГЛАВА 13
Движения.
§ 1. Понятие движения.
114.
○ Определение. Движением плоскости называется отображение плоскости на себя, сохраняющее расстояния.
○ Теорема. Осевая симметрия является движением.
○ Теорема. Центральная симметрия является движением.
● Теорема. При движении отрезок отображается на равный ему отрезок.
n Следствие. При движении треугольник отображается на равный ему треугольник.
115.
○ Теорема 1. Любое наложение является движением плоскости.
n Теорема 2. Любое движение является наложением.
n Следствие. При движении любая фигура отображается на равную ей фигуру.
§ 2. Параллельный перенос и поворот.
116.
○ Определение. Параллельным переносом на вектор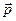 
называется такое отображение плоскости на себя, при котором любая точка М переходит в точку 
, такую что 
.
|
|
○ Теорема. Параллельный перенос является движением.
117.
○ Определение. Поворотом плоскости вокруг точки О на угол α называется такое отображение плоскости на себя, при котором любая точка М переходит в точку , такую что 
и угол 
равен α.
Теорема. Поворот является движением.
*****
ПРИЛОЖЕНИЯ
АКСИОМЫПЛАНИМЕТРИИ