§ 1. Перпендикулярность прямой и плоскости.
15.
○ Определение. Две прямые в пространстве называются перпендикулярными, если угол межу ними равен 90°.
● Лемма (о перпендикулярности двух параллельных прямых к третьей). Если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к ней.
16.
n Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Теорема. Если прямая перпендикулярна к плоскости, то она пересекает эту плоскость.
n Теорема (свойство параллельных прямых). Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
n Теорема(признак параллельных прямых). Если две прямые перпендикулярны к плоскости, то они параллельны.
17.
n Теорема (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
18.
n Теорема (о прямой перпендикулярной к плоскости). Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
○ Теорема (3 признак параллельности плоскостей (N 123)). Если две плоскости перпендикулярны к прямой, то они параллельны.
Теорема (6 свойство параллельных плоскостей (N 132)). Если одна из двух параллельных плоскостей перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой.
Теорема (N 133). Через любую точку пространства проходит только одна плоскость перпендикулярная к данной прямой.
Теорема (N 137). Через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость перпендикулярная к другой прямой.
|
|
§ 2. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
19.
○ Определение. Перпендикуляром, проведенным из точки к плоскости, называется отрезок, соединяющий данную точку с точкой на плоскости и лежащий на прямой, перпендикулярной плоскости.
○ Определение. Основанием перпендикуляра называется его конец, лежащий на плоскости.
○ Определение. Наклонной, проведенной из точки к плоскости, называется отрезок, соединяющий данную точку с какой-нибудь точкой на плоскости и не являющийся перпендикуляром к этой плоскости.
○ Определение. Основанием наклонной называется ее конец, лежащий на плоскости.
○ Определение. Проекцией наклонной на плоскость называется отрезок, соединяющий основание наклонной с основанием перпендикуляра, проведенного из той же точки к этой плоскости.
Замечание. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.
○ Определение. Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к этой плоскости.
n Замечание 1. Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
○ Определение. Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из этих плоскостей до другой плоскости.
n Замечание 2. Если прямая параллельна плоскости, то все точки этой прямой равноудалены от этой плоскости.
|
|
○ Определение. Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до этой плоскости.
○ Определение. Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
20.
n Теорема (о трех перпендикулярах). Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
n Теорема (обратная к теореме о трех перпендикулярах). Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
21.
Определение. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
○ Определение. Проекцией фигуры F на данную плоскость называется фигура F`, состоящая из проекций всех точек фигуры F на эту плоскость.
○ Теорема. Проекцией наклонной прямой на плоскость является прямая.
○ Следствие. Проекцией отрезка наклонной прямой на плоскость является отрезок.
● Определение. Углом между наклонной прямой и плоскостью называется угол между ней и ее проекцией на эту плоскость.
○ Определение. Угол между перпендикуляром и плоскостью считается равным 90°.
§ 2. Двугранный угол. Перпендикулярность плоскостей.
|
|
22.
Определение. Двугранным углом называется фигура образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
○ Определение. Гранями двугранного угла называются полуплоскости его образующие.
○ Определение. Ребром двугранного угла называется общая граница его граней.
○ Определение. Линейным углом двугранного угла называется угол, образованный двумя лучами, лежащими в разных его гранях и исходящими из одной точки на его ребре перпендикулярно к ребру.
Теорема (корректность определения линейного угла двугранного угла). Все линейные углы двугранного угла равны друг другу.
Определение. Градусной мерой двугранного угла называется градусная мера его линейного угла.
23.
n Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90°.
n Теорема (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
● Следствие. Если плоскость перпендикулярна к прямой, по которой пересекаются две данные плоскости, то она перпендикулярна к каждой из этих плоскостей.
24.
○ Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания являются прямоугольниками.
Теорема (1 свойство прямоугольного параллелепипеда). В прямоугольном параллелепипеде все шесть граней - прямоугольники.
Теорема (2 свойство прямоугольного параллелепипеда). Все двугранные углы прямоугольного параллелепипеда - прямые.
■ Теорема (3 свойство прямоугольного параллелепипеда). Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
■ Следствие (4 свойство прямоугольного параллелепипеда). Диагонали прямоугольного параллелепипеда равны.
○ Теорема (о двух плоскостях, перпендикулярных третьей (N 183)). Если две пересекающиеся плоскости перпендикулярны третьей, то их линия пересечения тоже ей перпендикулярна.
○ Теорема (об общем перпендикуляре к скрещивающимся прямым (N 186)). Существует одна и только одна прямая, пересекающая две данные скрещивающиеся прямые и перпендикулярная к каждой из них.
ГЛАВА 3
Многогранники
§ 1. Понятие многогранника. Призма.
25.
○ Определение. Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, причем никакие два соседних многоугольника не лежат в одной плоскости.
○ Определение. Гранями многогранника называются многоугольники, из которых составлен многогранник.
○ Определение. Ребрами многогранника называются стороны его граней.
○ Определение. Вершинами многогранника называются концы его ребер.
○ Определение. Диагональю многогранника называется отрезок, соединяющий две вершины, не принадлежащие одной грани.
○ Определение. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани.
○ Теорема. В выпуклом многограннике сумма всех плоских углов при его каждой вершине меньше 360°.
27.
○ Определение. n -угольной призмой называется призма, в основании которой лежит n -угольник.
○ Определение. Высотой призмы называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
○ Определение. Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям.
Замечание. Высота прямой призмы равна ее боковому ребру.
○ Определение. Призма называется наклонной, если ее боковые ребра не перпендикулярны к основаниям.
○ Определение. Призма называется правильной, если она прямая, и ее основания - правильные многоугольники.
○ Замечание. У правильной призмы все боковые грани - равные прямоугольники.
Определение. Площадью полной поверхности призмы называется сумма площадей всех ее граней.
Определение. Площадью боковой поверхности призмы называется сумма площадей всех ее боковых граней.
n Теорема (площадь боковой поверхности прямой призмы). Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Теорема (N 236)). Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
§ 2. Пирамида.
28.
○ Определение. n -угольной пирамидой называется пирамида, в основании которой лежит n -угольник.
Замечание. Треугольная пирамида - это тетраэдр.
○ Определение. Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Определение. Площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
Определение. Площадью боковой поверхности пирамиды называется сумма площадей всех ее боковых граней.
29.
Определение. Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок соединяющий вершину пирамиды с центром основания, является ее высотой.
○ Замечание 1. У правильной пирамиды все боковые грани - равные равнобедренные треугольники.
○ Замечание 2. У правильной пирамиды все боковые ребра равны.
○ Определение. Апофемой правильной пирамиды называется высота ее боковой грани, проведенная из вершины.
n Теорема (площадь боковой поверхности правильной пирамиды). Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
30.
○ Определение. Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
○ Замечание 1. У усеченной пирамиды все боковые грани - трапеции.
Определение. Площадью полной поверхности усеченной пирамиды называется сумма площадей всех ее граней.
Определение. Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.
Определение. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
○ Замечание 1. Основания правильной усеченной пирамиды - правильные многоугольники.
○ Замечание 2. Боковые грани правильной усеченной пирамиды - равнобедренные трапеции.
○ Определение. Апофемой правильной усеченной пирамиды называется высота ее боковой грани.
n Теорема (площадь боковой поверхности правильной усеченной пирамиды). Площадь боковой поверхности правильной усеченной пирамиды равна половине произведения полусуммы периметров оснований на апофему.
§ 3. Правильные многогранники.
31.
○ Определение. Точки А и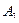 
называются симметричными относительно точки О (центра симметрии), если О - середина отрезка 
.
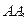○ Замечание. Точка О считается симметричной самой себе.
○ Определение. Точки А и 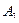называются симметричными относительно прямой а (оси симметрии), если прямая а - серединный перпендикуляр к отрезку 
.
○ Замечание. Каждая точка прямой а считается симметричной самой себе.
○ Определение. Точки А и 
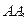называются симметричными относительно плоскости α (плоскости симметрии), если плоскость α проходит через середину отрезка и перпендикулярна ему.
○ Замечание. Каждая точка плоскости α считается симметричной самой себе.
○ Определение. Точка, (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке этой фигуры.
○ Определение. Элементами симметрии многогранника называются центр, оси и плоскости его симметрии.
32.
Определение. Выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и в каждой вершине сходится одно и то же число ребер.
○ Теорема. Не существует правильного многогранника, гранями которого являются правильные n -угольники при n >5.
○ Следствие. Существует 5 видов правильных многогранников:
правильный тетраэдр (состоящий из 4 равносторонних треугольников),
правильный октаэдр (состоящий из 8 равносторонних треугольников),
правильный икосаэдр (состоящий из 20 равносторонних треугольников),
куб (состоящий из 6 квадратов),
правильный додекаэдр (состоящий из 12 правильных пятиугольников).
*****
ГЕОМЕТРИЯ 11
ГЛАВА 4
Векторы в пространстве
§ 1. Понятие вектора в пространстве.
34.
○ Определение. Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом.
○ Определение. Нулевым вектором называется любая точка пространства.
○ Определение. Длиной ненулевого вектора называется длина соответствующего отрезка; длина нулевого вектора считается равной 0.
Определение. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
○ Определение. Два ненулевых вектора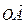 
и 
называются сонаправленными, если они коллинеарны и при этом лучи ОА и ОВ сонаправлены.
○ Определение. Два ненулевых вектора называются противоположно направленными, если они коллинеарны и не сонаправлены.
○ Замечание. Нулевой вектор сонаправлен с любым вектором.
35.
Определение. Векторы называются равными, если они сонаправлены и их длины равны.
Теорема. От любой точки можно отложить вектор, равный данному, и притом только один.
§ 2. Сложение и вычитание векторов. Умножение вектора на число.
36.
○ Определение. Суммой двух векторов называется вектор, полученный из них по правилу треугольника.
○ Теорема. Сумма векторов не зависит от выбора точки для откладывания векторов.
Теорема (правило треугольника). Для любых трех точек А, В и С имеет место равенство 
.
Теорема (законы сложения векторов). Для любых векторов 
, 
и 
справедливы равенства:
5. 
(переместительный закон);
6. 
(сочетательный закон).
○ Определение. Два ненулевых вектора называются противоположными, если они противоположно направлены и их длины равны.
Замечание. Вектором противоположным нулевому вектору, считается нулевой вектор.
○ Определение. Разностью векторов 
и называется вектор, сумма которого с вектором 
равна вектору .
○ Теорема. Для любых векторов и 
справедливо равенство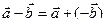 
.
37.
○ Теорема. Сумма нескольких векторов не зависит от порядка их сложения.
Теорема (правило многоугольника). Если , 
, …, 
- произвольные точки, то 
.
38.
○ Определение. Произведением ненулевого вектора 
на число k называется вектор 
, длина которого равна 
, причем вектор 
сонаправлен вектору при 
и противоположно направлен при k <0
○ Определение. Произведением нулевого вектора на любое число считается нулевой вектор.
○ Следствие 1. Произведение любого вектора на число 0 есть нулевой вектор.
○ Следствие 2. Для любого вектора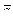 
и любого числа k векторы и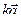 
коллинеарны.
○ Теорема (законы умножения вектора на число). Для любых векторов , 
и любых чисел k, l справедливы равенства:
4. 
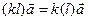(сочетательный закон).
5. 
(первый распределительный закон).
6. 
(второй распределительный закон).
○ Теорема. Для любого вектора справедливо равенство: 
.
○ Теорема. Если векторы и 
коллинеарны и 
, то существует (единственное) число k такое, что 
.
§ 2. Компланарные векторы.
39.
○ Определение. Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Следствие 1. Любые два вектора компланарны.
Следствие 2. Три вектора, среди которых имеются два коллинеарных, компланарны.
Теорема (признак компланарности векторов). Если вектор 
можно разложить по векторам 
и , т. е. представить в виде 
, где x и y - некоторые числа, то векторы , и 
компланарны.
○ Теорема (обратная к признаку компланарности векторов). Если векторы , и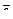 
компланарны, а векторы и не коллинеарны, то вектор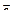 
можно разложить по векторам и , причем единственным образом.
41
● Теорема (о разложении вектора по трем некомпланарным векторам). Любой вектор можно разложить по трем данным некомпланарным векторам, причем единственным образом.
ГЛАВА 5