§ 1. Координаты точки и координаты вектора.
42.
○ Определение. Прямоугольная система координат называется заданной, если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление и единица измерения отрезков.
43.
○ Определение. Вектор называется единичным, если его длина равна единице.
○ Определение. Координатными векторами называются три единичных вектора, отложенные от начала координат так, чтобы направление одного из них совпало с направлением оси Ох, другого - оси Оу, а третьего - оси Оz.
○ Определение. Координатами вектора в данной системе координат называются коэффициенты в разложении этого вектора по координатным векторам.
○ Замечание 1. Координаты нулевого вектора равны нулю.
Замечание 2. Координаты равных векторов соответственно равны.
Теорема 1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Теорема 2. Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.
Теорема 3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
44.
○ Определение. Радиус-вектором данной точки называется вектор, конец которого совпадает с данной точкой, а начало - с началом координат.
Теорема. Координаты любой точки равны соответствующим координатам ее радиус-вектора.
Теорема (о координатах вектора). Каждая координата вектора равна разности соответствующих координат его конца и начала.
45.
Теорема 1 (о координатах отрезка). Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
○ Теорема 2 (о длине вектора). Длина вектора равна корню из суммы квадратов его координат. (Длина вектора 
вычисляется по формуле 
).
Теорема 3 (о расстоянии между двумя точками). Расстояние между точками 
и 
вычисляется по формуле 
.
§ 2. Скалярное произведение векторов.
46.
Определение. Два вектора называются перпендикулярными, если угол между ними равен 90°.
47.
Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Теорема. Скалярное произведение ненулевых векторов равно 0 тогда и только тогда, когда эти векторы перпендикулярны.
○ Определение. Скалярным квадратом вектора называется скалярное произведение вектора на себя.
○ Теорема. Скалярный квадрат вектора равен квадрату его длины.
Теорема. Скалярное произведение векторов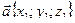 
и 
выражается формулой: 
.
Теорема. Ненулевые векторы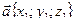 
и 
перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0 (
).
Теорема. Косинус угла между ненулевыми векторами 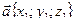и 
выражается формулой: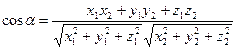 
.
○ Теорема (основные свойства скалярного произведения векторов). Для любых векторов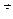 
, 
, 
и любого числа k справедливы соотношения:
3. 
, причем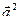 
>0 при 
;
4. 
(переместительный закон);
7. 
(распределительный закон);
8. 
(сочетательный закон).
48.
○ Определение. Направляющим вектором прямой называется ненулевой вектор, лежащий либо на этой прямой, либо на параллельной.
○ Теорема. Косинус угла между прямыми с направляющими векторами 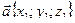и 
выражается формулой 
.
○ Теорема. Синус угла между прямой с направляющим вектором 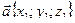и плоскостью с перпендикулярным ей вектором 
выражается формулой 
.
§ 3. Движения.
49.
Определение. Движением пространства называется отображение пространства на себя, сохраняющее расстояние между точками.
○ Определение. Центральной симметрией с центром О называется такое отображение пространства на себя, при котором любая точка пространства переходит в точку, симметричную ей относительно данного центра О.
Теорема. Центральная симметрия является движением.
50.
○ Определение. Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка пространства переходит в точку, симметричную ей относительно оси a.
Теорема. Осевая симметрия является движением.
51.
○ Определение. Зеркальной симметрией относительно плоскости α называется такое отображение пространства на себя, при котором любая точка пространства переходит в точку, симметричную ей относительно плоскости α.
Теорема. Зеркальная симметрия является движением.
52.
○ Определение. Параллельным переносом на вектор 
называется такое отображение пространства на себя, при котором любая точка М переходит в точку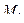 
, такую что 
.
Теорема. Параллельный перенос является движением.
ГЛАВА 6
Цилиндр, конус и шар
§ 1. Цилиндр.
53.
○ Теорема. Все образующие цилиндра параллельны и равны друг другу.
○ Теорема. Осевое сечение цилиндра является прямоугольником.
Теорема. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
54.
Определение. За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Определение. Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
○ Теорема. Площадь боковой поверхности цилиндра равна произведению длины окружности основания цилиндра на его высоту (
).
○ Теорема. Площадь полной поверхности цилиндра равна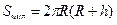 
.
§ 2. Конус.
55.
Теорема. Все образующие конуса равны друг другу.
○ Теорема. Осевое сечение конуса является равнобедренным треугольником.
○ Теорема. Если секущая плоскость перпендикулярна к оси конуса, то сечение является кругом с центром, расположенным на оси конуса.
56.
Определение. За площадь боковой поверхности конуса принимается площадь ее развертки.
Определение. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.
○ Теорема. Площадь боковой поверхности конуса равна половине произведения образующей конуса на длину окружности его основания (
).
○ Теорема. Площадь полной поверхности конуса равна 
.
57.
Теорема. Все образующие усеченного конуса равны друг другу.
○ !!!!!!!(отсутствует) Теорема. Осевое сечение усеченного конуса является равнобедренной трапецией.
○ Теорема. Если секущая плоскость перпендикулярна к оси усеченного конуса, то сечение является кругом с центром, расположенным на его оси.
○ !!!!!!!(отсутствует) Определение. За площадь боковой поверхности усеченного конуса принимается площадь ее развертки.
○ !!!!!!!(отсутствует) Определение. Площадью полной поверхности усеченного конуса называется сумма площадей боковой поверхности и оснований.
○ Теорема. Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей его оснований на образующую (
).
§ 3. Сфера.
58.
Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
○ Определение. Радиусом сферы называется любой отрезок, соединяющий центр сферы и какую-нибудь ее точку.
○ Определение. Диаметром сферы называется отрезок, соединяющий две точки сферы и проходящий через ее центр.
○ Определение. Шаром называется тело, ограниченное сферой.
○ Замечание. Шар с центром О и радиусом R содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R, и только эти точки.
59.
○ Определение. Уравнением поверхности называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты любой точки этой поверхности, и не удовлетворяют координаты никакой точки, не лежащей на ней.
○ Теорема (уравнение сферы). В прямоугольной системе координат уравнение сферы с центром 
и радиусом R имеет вид: 
.
60.
○ Теорема 1. Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечением сферы этой плоскостью является окружность.
○ Следствие. Сечением шара плоскостью является круг.
Теорема 2. Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.
Теорема 3. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
61.
○ Определение. Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку.
n Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
n Теорема. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
62.
○ Определение. Описанным около сферы многогранником называется многогранник, все грани которого касаются сферы.
○ Определение. Сфера называется вписанной в многогранник, если она касается всех его граней.
Определение. Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина пирамиды совпадает с вершиной конуса.
○ !!!!!(опечатка в учебнике) Определение. Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.
ГЛАВА 7
Объемы тел
§ 1. Объем прямоугольного параллелепипеда.
63.
○ Замечание 0. Объем куба со стороной 1 равен 1 кубической единице.
Замечание 1. Равные тела имеют равные объемы.
Замечание 2. Если тело составлено из нескольких тел, то его объем равен сумме их объемов.
Следствие. Объем куба с ребром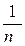 
равен 
.
64.
n Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
n Следствие 1. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
n Следствие 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
§ 2. Объем прямой призмы и цилиндра.
65.
n Теорема. Объем прямой призмы равен произведению площади основания на высоту.
66.
Определение. Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.
n Теорема. Объем цилиндра равен произведению площади основания на высоту 
: 
.
§ 3. Объем наклонной призмы, пирамиды и конуса.
67.
Теорема (основная формула для вычисления объемов тел). 
.
68.
n Теорема. Объем наклонной призмы равен произведению площади основания на высоту.
○ Теорема. Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения.
69.
n Теорема. Объем пирамиды равен одной трети произведения площади основания на высоту: 
.
● Следствие. Объем усеченной пирамиды вычисляется по формуле: 
.
70.
● Теорема. Объем конуса равен одной трети произведения площади основания на высоту: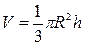 
.
.
● Следствие. Объем усеченного конуса вычисляется по формуле: 
.
§ 4. Объем шара и площадь сферы.
71.
n Теорема. Объем шара радиуса R равен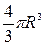 
.
72.
Определение. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
○ Определение. Высотой сегмента называется отрезок диаметра шара, заключенного внутри сегмента и перпендикулярного секущей плоскости.
Теорема. Объем шарового сегмента вычисляется по формуле: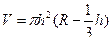 
.
Определение. Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.
○ Определение. Высотой шарового слоя называется расстояние между секущими плоскостями.
○ Теорема. Объем шарового слоя равен разности объемов двух шаровых сегментов.
○ Определение. Шаровым сектором называется тело, полученное вращением кругового сектора с острым углом, вокруг одного из ограничивающих его радиусов.
Теорема. Шаровой сектор состоит из шарового сегмента и конуса.
Теорема. Объем шарового сектора вычисляется по формуле 
.
73.
○ Теорема. Площадь сферы радиуса R равна 
.
*****
ПРИЛОЖЕНИЯ
АКСИОМЫСТЕРЕОМЕТРИИ