n Аксиома 1. Каждой прямой принадлежат по крайней мере две точки.
n Аксиома 2. Имеются по крайней мере три точки, не лежащие на одной прямой.
n Аксиома 3. Через любые две точки проходит прямая, и притом только одна.
n Аксиома 4. Из трех точек прямой одна, и только одна, лежит между двумя другими.
● Аксиома 5. Каждая точка О прямой разделяет ее на две части (два луча) так, что любые две точки одного луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О. При этом точка О не принадлежит ни одному из указанных лучей.
● Аксиома 6. Каждая прямая а, лежащая в плоскости, разделяет ее на две части (две полуплоскости) так, что любые две точки одной полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а. При этом точки прямой а не принадлежат ни одной из указанных полуплоскостей.
Аксиомы наложения.
n Аксиома 7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
n Аксиома 8. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
n Аксиома 9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
● Аксиома 10. Любой угол hk можно совместить наложением с равным ему углом 
двумя способами: 1) так, что луч h совместится с лучом 
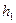, а луч k - с лучом 
; 2) так, что луч h совместится с лучом 
, а луч k - с лучом 
.
Аксиомы равенства.
n Аксиома 11. Любая фигура равна самой себе.
n Аксиома 12. Если фигура Ф равна фигуре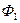 
, то фигура 
равна фигуре Ф.
n Аксиома 13. Если фигура 
равна фигуре 
, а фигура 
равна фигуре 
, то фигура 
равна фигуре 
.
|
|
Аксиомы измерения.
n Аксиома 14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
n Аксиома 15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
Аксиома параллельных прямых.
* ● Аксиома 16. В плоскости через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
○ Теорема (Чевы). Пусть в треугольнике АВС на сторонах ВС, СА и АВ или их продолжениях взяты соответственно точки 
, 
и 
, не совпадающие с вершинами треугольника. То прямые 
, 
и 
пересекаются в одной точке или попарно параллельны тогда и только тогда, когда выполнено равенство 
.
○ Теорема (Менелая). Пусть в треугольнике АВС на сторонах ВС, СА и АВ или их продолжениях взяты соответственно точки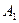 
, 
и 
, не совпадающие с вершинами треугольника. То точки 
, 
и 
лежат на одной прямой тогда и только тогда, когда выполнено равенство 
.
*****
ГЕОМЕТРИЯ 10-11
*****
ГЕОМЕТРИЯ 10
Введение
2.
n Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
● Аксиома 2. Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости.
● Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все их общие точки.
3.
n Теорема. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
|
|
n Теорема. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
ГЛАВА 1