ГЕОМЕТРИЯ
В ОПРЕДЕЛЕНИЯХ
И ТЕОРЕМАХ
ПОСОБИЕ
для повторения и изучения теоретического материала школьного курса геометрии
(по учебникам под редакцией Л.С. Атанасяна)
Данное пособие предназначено и для тех, кто повторяет курс школьной геометрии, и для тех, кто еще только изучает ее по учебникам «Геометрия 7-9» и «Геометрия 10-11» под редакцией Л.С. Атанасяна (2000-2007гг), возможно поможет оно и учителям, работающим по данным учебникам.
При повторении теоретического материала непосредственно по учебнику учащиеся обычно обращают внимание на факты, выделенные цветом, те же, которые расположены внутри текста, а, особенно, среди задач, просто выпадают из поля зрения.
В данном же пособии приведены практически все факты, встречающиеся на страницах учебника.
Кроме того, с учетом психологических особенностей процессов понимания и запоминания и используя принципы и методы структурной лингвистики, во многих формулировках изъяты вводные слова или дополнительные пояснения, а также изменен порядок слов, что при ПОЛНОМ соответствии тексту учебника по смыслу помогает намного быстрее и легче понять их и запомнить. Это подтвердил двадцатилетний опыт работы в школе.
Также в пособии отмечены факты, верные только на плоскости, на что, по понятным причинам, практически не обращается внимания в учебнике.
Кроме этого, исправлены ошибки учебника в формулировках и выделении фактов.
Для удобства пользования в пособии сохранены названия глав и параграфов учебника, нумерация пунктов и порядок следования фактов.
Обозначения, встречающиеся в данном пособии:
- n отмечены не измененные формулировки, выделенные в тексте учебника;
- отмечены не измененные формулировки, расположенные внутри текста учебника, обычно пропускаемые учащимися при повторении;
- ● отмечены измененные формулировки, выделенные в тексте учебника;
- ○ отмечены измененные формулировки, расположенные внутри текста учебника, обычно пропускаемые учащимися при повторении;
- полужирным шрифтом отмечены факты, не требующие доказательства;
- полужирным курсивом отмечены факты, требующие доказательства;
- выделены определяемые понятия для облегчения поиска;
- * отмечены факты, верные только на плоскости.
В заключение хочется выразить благодарность всем выпускникам и учителям гимназии 1567, принимавшим участие в создании этого пособия, а также учителям разных школ России за поддержку в осуществлении этого проэкта.
ГЕОМЕТРИЯ 7-9
*****
ГЕОМЕТРИЯ 7
ГЛАВА 1
Начальные сведения.
§ 1. Прямая и отрезок.
1.
■ Аксиома. Через любые две точки можно провести прямую, и притом только одну.
○ Определение. Две прямые называются пересекающимися, если они имеют общую точку.
Замечание. Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
○ Определение. Отрезком называется часть прямой, ограниченная двумя точками.
○ Определение. Концами отрезка называются точки, его ограничивающие.
§ 2. Луч и угол.
3.
○ Определение. Лучом, исходящим из точки О, называется каждая из двух частей, на которые точка О разделяет прямую.
○ Определение. Началом луча называется точка, из которой он исходит.
4.
○ Определение. Углом называется геометрическая фигура, состоящая из точки и двух лучей, исходящих из нее.
Определение. Угол называется развернутым, если обе его стороны лежат на одной прямой.
Замечание. Любой угол разделяет плоскость на две части.
○ Замечание. Луч делит угол на два угла, если он исходит из его вершины и проходит внутри угла.
§ 3. Сравнение отрезков и углов.
5.
Определение. Две геометрические фигуры называются равными, если их можно совместить наложением.
6.
○ Определение. Серединой отрезка называется точка, делящая его пополам.
○ Определение. Биссектрисой угла называется луч, исходящий из вершины угла и делящий его на два равных угла.
§ 4. Измерение отрезков.
7.
○ Замечание 1. За единицу измерения длины можно принять любой отрезок.
○ Замечание 2. Длина выражается некоторым положительным числом.
Замечание 3. Равные отрезки имеют равные длины.
Замечание 4. Меньший отрезок имеет меньшую длину.
○ Замечание 5. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.
○ Определение. Расстоянием между концами отрезка называется длина этого отрезка.
§ 5. Измерение углов.
9.
○ Определение. Градусом называется угол, равный 1/180 части развернутого угла.
○ Определение. Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
○ Замечание 1. За единицу измерения градусной меры принят градус.
○ Замечание 2. Градусная мера выражается некоторым положительным числом.
Замечание 3. Равные углы имеют равные градусные меры.
Замечание 4. Меньший угол имеет меньшую градусную меру.
○ Замечание 5. Если луч делит угол на два угла, то градусная мера всего угла равна сумме градусных мер этих двух углов.
Замечание 1. Развернутый угол равен 180°.
Замечание 2. Неразвернутый угол меньше 180°.
Определение. Угол называется прямым, если он равен 90°.
○ Определение. Угол называется тупым, если он больше 90°, но меньше 180°.
○ Определение. Угол называется острым, если он меньше 90°.
§ 6. Перпендикулярные прямые.
11.
○ Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются продолжениями друг друга.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Определение. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Теорема(свойство вертикальных углов). Вертикальные углы равны.
12.
○ Определение. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
* ○ Теорема. Если две прямые перпендикулярны третьей, то они не пересекаются.
ГЛАВА 2
Треугольники.
§ 1. Первый признак равенства треугольников.
14.
○ Определение. Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
○ Определение. Периметром треугольника называется сумма длин всех его сторон.
○ Замечание 1. В равных треугольниках против равных сторон лежат равные углы.
○ Замечание 2. В равных треугольниках против равных углов лежат равные стороны.
15.
■ Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
§ 2. Медианы, биссектрисы и высоты треугольника.
16.
○ Определение. Перпендикуляром, проведенным из точки к прямой, называется отрезок, соединяющий данную точку и точку на данной прямой и лежащий на прямой, перпендикулярной данной.
○ Определение. Основанием перпендикуляра, проведенного из точки к прямой, называется его конец, лежащий на данной прямой.
■ Теорема (о единственности перпендикуляра к прямой). Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
17.
○ Определение. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
○ Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
○ Определение. Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
18.
○ Определение. Треугольник называется равнобедренным, если у него две стороны равны.
○ Определение. Боковыми сторонами равнобедренного треугольника называются его равные стороны.
○ Определение. Треугольник называется равносторонним, если все его стороны равны.
■ Теорема (1 свойство равнобедренного треугольника). В равнобедренном треугольнике углы при основании равны.
■ Теорема (2 свойство равнобедренного треугольника). В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
● Следствие 1. В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
● Следствие 2. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
§ 3. Второй и третий признаки равенства треугольников.
19.
■ Теорема (второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
20.
■ Теорема (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
§ 4. Задачи на построение.
21.
* ● Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
* ○ Определение. Центром окружности называется точка равноудаленная от всех точек окружности.
○ Определение. Радиусом окружности называется отрезок, соединяющий центр окружности с какой-нибудь ее точкой.
○ Определение. Хордой называется отрезок, соединяющий две точки окружности.
○ Определение. Диаметром окружности называется хорда, проходящая через ее центр.
○ Определение. Дугой окружности называется каждая из двух частей, на которые две точки делят окружность.
○ Определение. Кругом называется часть плоскости, ограниченная окружностью.
ГЛАВА 3
Параллельные прямые.
§ 1. Признак параллельности двух прямых.
24.
* ■ Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
25.
○ Определение. Прямая называется секущей по отношению к двум прямым, если она пересекает обе эти прямые.
● Теорема (1 признак параллельности двух прямых). Если две прямые пересечены секущей и накрест лежащие углы равны, то прямые параллельны.
● Теорема (2 признак параллельности двух прямых). Если две прямые пересечены секущей и соответственные углы равны, то прямые параллельны.
● Теорема (3 признак параллельности двух прямых). Если две прямые пересечены секущей и сумма односторонних углов равна 180°, то прямые параллельны.
§ 2. Аксиома параллельных прямых.
28.
* ● Аксиома (параллельных прямых). На плоскости через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
* ● Следствие 1. На плоскости если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
● Следствие 2 (4 признак параллельности двух прямых). Если две прямые параллельны третьей, то они параллельны.
29.
■ Теорема (1 свойство параллельности двух прямых). Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
■ Следствие. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
■ Теорема (2 свойство параллельности двух прямых). Если две параллельные прямые пересечены секущей, то соответственные углы равны.
■ Теорема (3 свойство параллельности двух прямых). Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
ГЛАВА 4
Соотношения между сторонами и углами треугольника.
§ 1. Сумма углов треугольника.
30.
■ Теорема (о сумме углов треугольника ). Сумма углов треугольника равна 180°.
○ Определение. Гипотенузой называется сторона прямоугольного треугольника, лежащая против прямого угла.
Определение. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Теорема (о внешнем угле треугольника ). Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
31.
○ Теорема. В треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
○ Определение. Треугольник называется остроугольным, если все его углы острые.
○ Определение. Треугольник называется тупоугольным, если один его угол тупой.
○ Определение. Треугольник называется прямоугольным, если один его угол прямой.
○ Определение. Гипотенузой называется сторона прямоугольного треугольника, лежащая против прямого угла.
○ Определение. Катетом называется сторона прямоугольного треугольника, прилежащая к прямому углу.
§ 2. Соотношения между сторонами и углами треугольника.
32.
● Теорема (о соотношениях межу сторонами и углами треугольника ). В треугольнике: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона.
■ Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
● Следствие 2 (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.
33.
■ Теорема (неравенство треугольника ). Каждая сторона треугольника меньше суммы двух других.
■ Следствие 2. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ<АС+СВ, АС<АВ+СВ, ВС<АС+АВ.
§ 3. Прямоугольные треугольники.
34.
● Теорема (1 свойство прямоугольных треугольников ). В прямоугольном треугольнике сумма острых углов равна 90°.
● Теорема (2 свойство прямоугольных треугольников ). В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
● Теорема (3 свойство прямоугольных треугольников ). Если в прямоугольном треугольнике катет равен половине гипотенузы, то угол, лежащий против него, равен 30°.
35.
■ Теорема (1 признак равенства прямоугольных треугольников ). Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
■ Теорема (2 признак равенства прямоугольных треугольников ). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
■ Теорема (3 признак равенства прямоугольных треугольников ). Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
■ Теорема (4 признак равенства прямоугольных треугольников ). Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
§ 4. Построение треугольника по трем элементам.
37.
○ Определение. Наклонной, проведенной из точки к прямой, называется отрезок, соединяющий эту точку и точку на прямой и не являющийся перпендикуляром к этой прямой.
○ Теорема (о перпендикуляре и наклонной). Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
○ Определение. Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой.
● Теорема. Если две прямые параллельны, то все точки одной прямой равноудалены от другой.
○ Определение. Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из них до другой.
* ○ Замечание. Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой, параллельной данной.
*****
ГЕОМЕТРИЯ 8
○●
ГЛАВА 5
Четырехугольники
§ 1. Многоугольники.
39.
○ Определение. Смежными отрезками называются отрезки, имеющие один общий конец.
* ○ Определение. Многоугольником называется геометрическая фигура на плоскости, составленная из отрезков АВ, ВС, …, EF, FA так, что смежные отрезки не лежат на одной прямой, а не смежные отрезки не имеют общих точек.
○ Определение. Сторонами многоугольника называются отрезки, из которых он состоит.
○ Определение. Вершинами многоугольника называются концы его сторон.
○ Определение. Периметром многоугольника называется сумма длин всех его сторон.
○ Определение. n -угольником называется многоугольник с n вершинами.
○ Определение. Соседними вершинами многоугольника называются две его вершины, принадлежащие одной стороне.
○ Определение. Диагональю многоугольника называется отрезок, соединяющий любые две его несоседние вершины.
40.
○ Определение. Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, проходящей через две его соседние вершины.
○ Теорема. Сумма углов выпуклого n -угольника равна 180°(n -2).
41.
○ Определение. Противоположными сторонами четырехугольника называются две его несмежные стороны.
○ Определение. Противоположными вершинами четырехугольника называются две его несоседние вершины.
Теорема. Сумма углов выпуклого четырехугольника равна 360°.
§ 2. Параллелограмм и трапеция.
42.
n Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема. Параллелограмм является выпуклым четырехугольником.
n Теорема (1 свойство параллелограмма). В параллелограмме противоположные стороны равны и противоположные углы равны.
● Теорема (2 свойство параллелограмма). В параллелограмме диагонали делятся точкой пересечения пополам.
43.
● Теорема (1 признак параллелограмма). Если в четырехугольнике две стороны равны и параллельны, то это - параллелограмм.
● Теорема (2 признак параллелограмма). Если в четырехугольнике противоположные стороны попарно равны, то это - параллелограмм.
● Теорема (3 признак параллелограмма). Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то это - параллелограмм.
44.
○ Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие нет.
○ Определение. Основаниями трапеции называются две ее параллельные стороны.
○ Определение. Боковыми сторонами трапеции называются две ее не параллельные стороны.
n Определение. Трапеция называется равнобедренной, если ее боковые стороны равны.
○ Определение. Трапеция называется прямоугольной, если один из ее углов прямой.
Теорема (Фалеса (N 385)). Если на одной из двух прямых последовательно отложить несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
§ 3. Прямоугольник, ромб, квадрат.
45.
n Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
● Теорема (свойство прямоугольника). В прямоугольнике диагонали равны.
● Теорема (признак прямоугольника). Если в параллелограмме диагонали равны, то это - прямоугольник.
46.
n Определение. Ромбом называется параллелограмм, у которого все стороны равны.
● Теорема (свойство ромба). В ромбе диагонали взаимно перпендикулярны и делят его углы пополам.
○ Теорема (1 признак ромба (N 408)). Если в параллелограмме диагонали
взаимно перпендикулярны, то это - ромб.
○ Теорема (2 признак ромба (N 408)). Если в параллелограмме диагональ
является биссектрисой его угла, то это - ромб.
n Определение. Квадратом называется прямоугольник, у которого все стороны равны.
● Теорема (1 свойство квадрата). В квадрате все углы прямые.
● Теорема (2 свойство квадрата).  В квадрате диагонали равны, взаимно
В квадрате диагонали равны, взаимно
перпендикулярны и делят его углы пополам.
47.
○ Определение. Две точки А и А 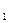 называются симметричными относительно прямой а, если эта прямая - серединный перпендикуляр к отрезку АА
называются симметричными относительно прямой а, если эта прямая - серединный перпендикуляр к отрезку АА 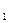 .
.
○ Замечание. Каждая точка оси симметрии считается симметричной сама себе.
○ Определение. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры точка, симметричная ей относительно прямой а, также принадлежит фигуре.
○ Определение. Две точки А и А 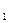 называются симметричными относительно точки О, если эта точка - середина отрезка АА
называются симметричными относительно точки О, если эта точка - середина отрезка АА 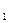 .
.
○ Замечание. Точка - центр симметрии считается симметричной сама себе.
○ Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры точка, симметричная ей относительно точки О, также принадлежит фигуре.
ГЛАВА 6
Площадь
§ 1. Площадь многоугольника.
48.
○ Не определение! Площадь многоугольника - это величина той части плоскости, которую занимает многоугольник.
○ Замечание 0. Площадь квадрата со стороной 1 равна 1 квадратной единице.
n Замечание 1. Равные многоугольники имеют равные площади.
● Замечание 2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме их площадей.
n Замечание 3. Площадь квадрата равна квадрату его стороны.
50.
n Теорема (площадь прямоугольника). Площадь прямоугольника равна произведению его смежных сторон.
§ 2. Площади параллелограмма, треугольника и трапеции.
51.
○ Определение. Основанием параллелограмма называется одна из его сторон.
○ Определение. Высотой параллелограмма называется перпендикуляр, проведенный к прямой, содержащей основание, из любой точки противоположной стороны.
n Теорема (площадь параллелограмма). Площадь параллелограмма равна произведению его основания на высоту.
52.
○ Определение. Основанием треугольника называется одна из его сторон.
● Теорема (площадь треугольника). Площадь треугольника равна половине произведения его основания на высоту, проведенную к нему.
n Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.
n Следствие 2. Если высоты треугольников равны, то их площади относятся как основания.
● Теорема (об отношении площадей треугольников, имеющих по равному углу). Если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы.
53.
○ Определение. Высотой трапеции называется перпендикуляр, проведенный из любой точки одного основания к прямой, содержащей другое основание.
n Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту.
§ 3. Теорема Пифагора.
54.
n Теорема (Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
55.
n Теорема (обратная теореме Пифагора). Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
○ Определение. Пифагоровыми треугольниками называются прямоугольные треугольники, у которых длины сторон выражаются целыми числами.
ГЛАВА 7
Подобные треугольники
§ 1. Определение подобных треугольников.
56.
○ Определение. Отношением отрезков АВ и СD называется отношение их длин.
○ Определение. Отрезки АВ и CD называются пропорциональными отрезкам A 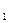 B
B 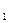 и C
и C 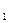 D
D 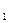 , если
, если 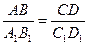 .
.
57.
○ Определение. Если все углы одного треугольника соответственно равны углам другого треугольника, то сходственными сторонами называются стороны этих треугольников, лежащие против соответственно равных углов.
n Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
○ Определение. Коэффициентом подобия называется число, равное отношению сходственных сторон подобных треугольников.
58.
n Теорема (об отношении площадей подобных треугольников). Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
○ Теорема (Свойство биссектрисы треугольника (N 535)). Биссектриса треугольника делит противоположную сторону треугольника на отрезки, пропорциональные прилежащим сторонам треугольника.
§ 2. Признаки подобия треугольников.
59.
● Теорема (1 признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
60.
n Теорема (2 признак подобия треугольников). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
61.
● Теорема (3 признак подобия треугольников). Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
○ Теорема (Фалеса, расширенная (N 556)). Если стороны угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной его стороне, пропорциональны отрезкам, отсекаемым на другой его стороне.
§ 3. Применение подобия к доказательству теорем и решению задач.
62.
Определение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
● Теорема (Свойство средней линии треугольника). Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
○ Теорема (Свойство медиан треугольника). Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
63.
○ Теорема. Высота прямоугольного треугольника, проведенная к гипотенузе, разделяет треугольник на два подобных треугольника, каждый из которых подобен данному треугольнику.
○ Определение. Средним пропорциональным между отрезками AB и CD (или средним геометрическим) называется отрезок XY, если  .
.
○ Замечание 1 (свойство высоты прямоугольного треугольника). Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу.
○ Замечание 2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между этим катетом и высотой, проведенной к гипотенузе.
§ 4. Соотношения между сторонами и углами прямоугольного треугольника.
66.
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Определение. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
○ Определение. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
○ Замечание 1. Тангенс угла равен отношению синуса этого угла к косинусу.
○ Замечание 2. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны соответственно.
Теорема (основное тригонометрическое тождество).