При решении задачи линейного программирования достаточно часто оптимального решения получить не удается. Это происходит по двум причинам. Назовите их. 3 глава

Все остальные характеристики — структура производства и сочетание отраслей, учет агробиологических и зоотехнических требований к производству, структура основных фондов и дру­гие— в задаче не должны учитываться, так как они уже оп­ределены как оптимальные, свойственные именно данному про­изводственному типу предприятия. Таким образом, размер­ность задачи резко сокращается без снижения качества ин­формации, на основе которой осуществляется решение задачи второго этапа по оптимальному размещению и специализации сельскохозяйственного производства по территории.

3. Планирование загрузки производственных мощностей. Модель оптимального плана загрузки оборудования. Основной целью управления производством является обеспечение заданной маркетинговой стратегии при минимальных издержках производства. Это достигается путем успешного решения локальных задач, что предполагает, что при решении каждой из них достигается свой оптимум и все локальные критерии согласуются с глобальной целью.

Такими локальными задачами в области производства являются:

- определение плана производства затрат на текущий ремонт;

- расчет норм затрат на эксплуатацию оборудования и определение срока его эксплуатации;

- определение издержек на приобретение сырья и материалов;

- оптимизация расходов по оплате труда путем определения рациональной величины затрат на социальное обеспечение работников, а также на наем и увольнение персонала.

Модель определения оптимального плана производства. В системе "Дельта", как и на реальном предприятии, работающем в условиях рыночной экономики, критерием оптимизации является не максимизация объема выпуска, а максимизация прибыли. При нахождении оптимума в сфере произ­водства приняты следующие допущения:

- объем сбыта продукции является функцией от цены и затрат на инструменты маркетинга, которые влияют на величину производственных издержек и, следовательно, учитываются при расчете прибыли;

- доходы предприятия от прочей непроизводственной деятельности (как, например, ссуда капитала) при планировании производства не принимаются в расчет;

- расходы предприятия, связанные с его финансовой деятельностью (заем капитала) также не принимаются в расчет. Они учитываются при нахождении оптимальных параметров в сфере финансирования.

Рассмотрим теперь формулу расчета прибыли предприятия, определенную без учета результата непроизводственной деятельности предприятия, эта формула является целевой фун­кцией указанной выше модели:

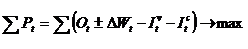(3.1)

где Р - прибыль (валовая прибыль после вычета переменных и условно-постоянных издержек производства) без учета внепроизводственных доходов и расходов;

О_t - оборот (выручка) в периоде t;

DW_t - изменение запасов сырья и готовой продукции (в стоимостном выражении) в периоде t, "+" - при уве­личении, "-" - при снижении;

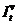- переменные издержки в периоде t, относимые на се­бестоимость единицы продукции;

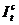- условно-постоянные издержки периода t (они не относятся на себестоимость продукции, но могут уве­личиваться или уменьшаться при изменении объема производства).

Оборот находится, как произведение объема сбыта на цену л, следовательно, не имеет прямой зависимости от объема про­изводства:

 

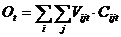(3.2)

 

где V_ijt - сбыт продукции i на рынке j в период t;

C_ijt - цена продукции i на рынке j в период t.

Ограничения модели:

1) Если объем возможного сбыта предприятия в период t, рассчитанный на основе исследований, окажется больше имею­щегося наличия, то реальный сбыт предприятия будет равен объему запаса. После проверки этого условия в программе происходит перерасчет реального объема сбыта для каждого предприятия;

2) ограничение по оборудованию:

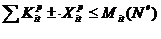(3.3)

где 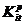- производственные коэффициенты загрузки станка типа l для производства продукции вида I;

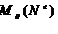- суммарная мощность станков типа l в период t, которая является функцией от нормы затрат на эксплуатацию оборудования (N^е);

3) условие неотрицательности объемов производства в пе­риод t:

Необходимо учитывать, что производственные коэффици­енты оборудования, коэффициенты потребления сырья и вы­работка рабочих изменяются в каждом периоде под воздей­ствием эффекта накопленного опыта.

Рассмотренная выше модель подсистемы производства пред­приятия является скорее описательной, чем пригодной для аналитического нахождения оптимального плана. Модель слишком сложна, чтобы свести ее к известной задаче, решае­мой аналитическими методами. Более того, найденный план в любом случае может стать оптимальным лишь для текущего периода, но не для длительного промежутка времени.

Определение оптимальной нормы затрат на эксплуатацию оборудования. Расходы по содержанию оборудования в период состоят из амортизационных отчислений и затрат на эксплуатацию оборудования.

Определение оптимального срока эксплуатации оборудования. В вопросе об оптимальном сроке эксплуатации каждого станка исходят изменения того, что утилизируемый станок всегда заменяется новым, равноценным.

Оптимальный срок эксплуатации достигается тогда, когда стоимость капитала, определяемая как разность между поступлениями от амортизационных отчислений и утилизации оборудования и затратами на приобретение и эксплуатацию достигает своего максимума.

 

Контрольные вопросы:

 

1. Как построить интегрированную схему модели?

2. Перечислите принципы построения интегрированной системы моделей.

3. По какому критерию производят расчет — мини­мум производственных затрат?

4. Перечислите локальные задачи в области производства.

 

Лекция № 4

 

МОДЕЛИРОВАНИЕ АГРОИНЖЕНЕРНЫХ ПРОЦЕССОВ.

МОДЕЛИРОВАНИЕ ОПТИМАЛЬНОГО СОСТАВА МАШИННО-ТРАКТОРНОГО ПАРКА

 

1. Постановка задачи. Система переменных и ограничений, критерий оптимальности.

2. Подготовка входной информации. Построение структурной и числовой экономико-математической модели задачи.

3. Решение задачи на компьютере. Анализ результатов решения задачи.

1. Постановка задачи. Система переменных и ограничений, критерий оптимальности. Для осуществления комплексной меха­низации сельскохозяйственного производства необходимо опре­делить оптимальный состав машинно-тракторного парка, то есть установить наиболее целесообразное соотношение между отдельными типами и марками тракторов и сельскохозяйствен­ных машин и их количеством вусловиях конкретного хозяйст­ва, района, зоны, которое обеспечит выполнение всего комп­лекса (заданного объема) сельскохозяйственных работ в уста­новленные агротехнические сроки и с наименьшими затратами. Применение экономико-математических методов и ЭВМ при решении данной задачи весьма эффективно, так как позволяет одновременно учесть все экономические и агротехнические условия и найти наилучший вариант, что практически невозмож­но с помощью обычных методов. Возможность использования этих методов обусловлена тем, что все необходимые экономи­ческие и агротехнические условия выражают с помощью ли­нейных неравенств и уравнений. Как линейная может быть записана и целевая функция — математическое выражение кри­терия оптимальности.

В качестве критериев оптимальности используют:

1) мини­мум приведенных затрат на выполнение заданного объема ра­бот;

2) минимум текущих затрат;

3) минимум капитальных вложений на приобретение тракторов и сельскохозяйственной техники;

4) минимум энергомашин;

5) минимум расхода топли­ва и др.

В одних и тех же экономических условиях, выражен­ных в ограничениях задачи, при использовании различных кри­териев будут получены различные варианты состава машинно-тракторного парка. Например, критерий «минимум текущих за­трат» не учитывает эффективности капитальных вложений и при его использовании для выполнения необходимого объема работ потребуется больше капитальных вложений и больше техники. Критерий «минимум капитальных вложений» не учи­тывает прямых, текущих затрат на выполнение работ, и по­следние значительно возрастают по сравнению с вариантом, рассчитанным по критерию «минимум текущих затрат». При­мерно такие же результаты получают при использовании кри­терия «минимум энергомашин» — возрастают текущие затра­ты на выполнение работ.

Экономически наиболее обоснованным является критерий «минимум приведенных затрат на выполнение работ и приоб­ретение техники». Приведенные затраты S представляют собой сумму текущих затрат на содержание и эксплуатацию машинно-тракторного парка и его балансовой стоимости, умноженной на нормативный коэффициент эффективности:

 

S = C+E×К, (4.1)

 

где С - текущие эксплуатационные затраты;

К - затраты на приобретение данного вида техники (балансовая стоимость);

Е - нормативный коэффициент эффективности капитальных вложений Нормативный коэффициент эффективности является величиной, обратной нормативному периоду окупаемости. Напри­мер, новый трактор должен окупиться за 6,6 года работы, тог­да нормативным коэффициент эффективности будет 1:66 =0,15.

Для конкретного сельскохозяйственного предприятия могут быть решены следующие задачи.

1. Определение оптимального состава машинно-тракторного парка для вновь организуемого хозяйства или подразделения (оптимальное комплектованиепарка). Для уже существующих хозяйств эта задача решается, как правило, на далекую перспективу, превышающую срок службы имеющейся техники.

2. Определение оптимального состава машинно-тракторного парка при условии, что в хозяйстве имеется некоторый набор тракторов и машин (оптимальное доукомплектованиепарка при заданном объеме работ и наличии средств на приобретение новой техники). Задача решается чаще всего на текущий период или на 3—5 лет. Возможно списание некоторых машин, по которым затраты на содержание и эксплуатацию выше эффекта от использования.

3. Определение плана наилучшего использованияимеющегося в хозяйстве парка путем оптимального распределения заданных работ между тракторными агрегатами. Эта задача решается на текущий период. Ставится условие, что хозяйство не имеет возможности купить новую технику. Может быть предусмотрено списание устаревших машин.

Система переменных. В задаче по оптимальному комплекто­ванию машинно-тракторного парка 2 группы переменных: чис­ло агрегатов, выполняющих технологические операции в опре­деленный расчетный период; число приобретаемых тракторов и сельскохозяйственных машин. В модели по оптимальному до­укомплектованию парка дополнительно может быть предусмотрена группа переменных, обозначающих число выбывающих (списываемых) тракторов и машин. В задаче по оптимальному использованию имеющегося машинно-тракторного парка отсутствуют переменные по приобретению новой техни­ки, но могут вводиться переменные по выбывающим машинам.

Система ограничений. Во всех моделях 2 или 3 группы ограничений: по обязательному выполнению работ в расчетные периоды; балансу использования тракторного парка (число тракторов и сельскохозяйственных машин каждой марки должно обеспечивать выполнение всех видов работ во все периоды); выполнению технологически связанных между собой работ и определенной последовательности.

Технико-экономическими коэффициентами в первой группе ограничений по группе переменных, обозначающих число агрегатов, являются показатели их производительности на каждой работе в каждом периоде. Константы в этих ограничениях обозначают объемы выполняемых работ.

Технико-экономическими коэффициентами во второй группе ограничений по переменным, обозначающим число агрегатов, являются целые числа, показывающие наличие сельскохо­зяйственных машин в агрегате (чаще всего коэффициенты рав­ны 1, поскольку с одним трактором, как правило, работает одна машина). По переменным, обозначающим количество по­купаемых тракторов и машин, ставится коэффициент —1, а по выбываемым маркам +1. Константами во второй группе огра­ничений в задаче по оптимальному комплектованию парка яв­ляются нули (поскольку никакого парка нет), а в задаче по доукомплектованию и использованию машинно-тракторного парка — наличие тракторов по учитываемым маркам.

Задачи могут быть решены с помощью симплексного мето­да линейного программирования. Разработаны также другие методы решения.

Разработка числовой модели. Исходная информация, расчет технико-экономических коэффициентов, констант и коэффици­ентов целевой функции.Методику составления числовой модели покажем на модели оптимального доукомплектования машин­но-тракторного парка — наиболее часто используемой в прак­тике текущего и перспективного планирования сельскохозяйст­венного производства.

В качестве источников исходной информации для построе­ния модели выступают:

- годовые производственно-финансовые и пятилетние планы развития сельскохозяйственного предприятия, план организа­ционно-хозяйственного устройства, хозрасчетные задания по бригадам и отделениям хозяйства; из этих источников получа­ют данные о структуре производства в колхозе или совхозе, посевных площадях в соответствии с принятыми в хозяйстве (бригаде) севооборотами, марках тракторов, автомобилей, сельскохозяйственных машин и орудий и их числе;

- технологические карты по возделыванию и уборке сельско­хозяйственных культур и угодий; с их помощью определяют перечень всех технологических операций при возделывании и уборке культур, объемы работ (га, т), календарные сроки их выполнения (начало, конец и продолжительность в днях), со­став и производительность различных агрегатов на операциях, данные о затратах труда и размерах эксплуатационных затрат на проведение сельскохозяйственных работ различными агре­гатами;

- нормативные справочники; из них берут данные о балансо­вой стоимости дополнительно приобретаемой техники и остаточной стоимости техники, которая может быть списана, об оплате труда, расходе топлива и смазочных материалов, затратах на хранение и содержание техники, нормативном коэффициенте эффективности и др.

2. Подготовка входной информации. Построение структурной и числовой экономико-математической модели задачи. Пройдут годы, века, тысячелетия, а такая постановка задачи сохранится независимо оттого, что будут проектировать, потому что при проектировании объективно существует одна из двух постановок: либо спроектировать изделие заданной стоимости с наилучшими свойствами, либо спроектировать изделие с заданными свойствами, но наименьшей стоимости.

Какая-либо другая постановка задачи проектирования просто невозможна, и поэтому попытка ставить задачу проектирования как-то иначе приводит лишь к излишней трате ресурсов и времени. Наилучшее решение этих задач может быть получено лишь с помощью методов оптимального проектирования, о которых не знали не только дикари, но которые неизвестны, к сожалению, и многим нашим современникам.

Все это следствие того, что при решении возникающих споров не используют понятие критерий. Но пока еще никому неизвестно, что, не выбрав критерия, любое решение принимать очень трудно, а оптимальное просто невозможно. Ведь оказывается, что перед тем как принять решение, надо знать, что мы хотим. А хотим мы, как правило, чтобы все было лучше. При этом не всегда знаем, что мы понимаем как под словом "все", так и под словом "лучше". Если смысл этих слов не определен, значит, критерий не принят. А если критерий не принят, то и оптимального решения быть не может.

Оказывается, что при решении почти каждого вопроса необходимо знать ответы на бесчисленные дополнительные вопросы, которые можно объединить в две группы: «а что будет, если...» и «а что надо, чтобы...»

Человек хорошо или плохо решает все возникающие перед ним задачи. Процесс принятия решений может быть неформализованным и формализованным. Принятие неформализованных решений - это творчество, если угодно, искусство.

Чтобы принять неформализованное решение, человеку зачастую ничего не надо. Есть вопрос. Пусть даже не совсем четкий. Сел, подумал, решил. Правда, никакой гарантии правильности решения при этом нет. Достаточно часто человек принимаем решение вообще без всяких обоснований, руководствуясь так называемым здравым смыслом, опытом, интуицией и другими аналогичными понятиями, которые никому совершенно ничего не объясняют. А потом для убедительности и убеждения самого себя и других придумывают достаточно веские и обоснованные причины, доказывающие правильность интуитивно принятого решения.

Что же касается формализованных решений, то они принимаются по четким рекомендациям. При этом различные люди, руководствуясь этими рекомендациями, будут принимать одни и те же решения. Принятие формализованных решений - наука. Этому можно научить.

Очевидно, что с помощью подобных уточнений можно давать достаточно конкретные рекомендации по принятию решений в весьма сложных ситуациях.

Принятие оптимальных решений базируется на «трех китах»: математической модели; решении задачи на компьютере; исходных данных. Начнем с "кита №1" - математической модели. Математика всегда пыталась давать ответы на возникающие вопросы. И если, сравнительно недавно, надо было подсчитать число еде данных топоров, то теперь математику используют и для принятия оптимальных решений.

Математическое моделирование имеет два существенных преимущества: дает быстрый ответ на поставленный вопрос, на что в реальной обстановке могут потребоваться иногда даже годы; предоставляет возможность широкого экспериментирования, осуществить которое на реальном объекте зачастую просто невозможно.

Составление математической модели начинается с содержательной постановки задачи. На этом этапе приходится иметь дело со специалистами в предметной области (по управлению, проектированию, разработке технологических процессов и т. д.) Эти специалисты - люди, как правило, очень добросовестные, однако, прекрасно зная свой предмет, не всегда имеют представление о том, что именно требуется для принятия оптимального решения. Поэтому содержательная постановка задачи зачастую оказывается перенасыщенной сведениями, которые для постановки задачи совершенно излишни.

Но в жизни, к сожалению, не всегда бывает легко отделимо главное от второстепенного и составить приемлемую математическую модель. Составление модели - это искусство, творчество. До какого-то уровня научить можно, но не более того.

А там, где творчество, очень важны личные качества: знания, способности, если угодно, талант.

Если двое смотрят на одно и то же, это не означает, что оба видят одно и то же. И слова древних греков "Если двое делают одно и то же, это не значит, что получится одно и то же" в полной мере относятся к составлению математических моделей. Не вызывает сомнения, что для успешного принятия оптимального решения необходимо знать, что такое математическая модель, и представлять каким образом компьютер находит это решение.

Если модель описывает зависимость между исходными данными и искомыми величинами, то алгоритм представляет собой последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам.

Алгоритмы задач принятия решений настолько сложны, что без применения компьютера реализовать их практически невозможно. Итак, мы подошли ко "второму киту" - компьютеру. Компьютер с помощью программного обеспечения реализует алгоритмы поиска оптимального решения, которые преобразуют исходные данные в искомый результат.

И, наконец, "третий кит" - исходные данные. Никакая хорошая сходимость алгоритма, никакое быстродействие и оперативная память компьютера не заменят достоверности исходных данных. По этому поводу можно было бы сказать много правильных слов, но мы ограничимся лишь тем, что приведем хорошо известную пословицу: что посеешь, то и пожнешь! От себя добавим: и никакие комбайны (то есть математические модели и программы) не заменят качественных семян!

Для составления модели возьмем самое простое изделие. Это будет даже не кувшин, форму которого описать достаточно трудно. Будем проектировать бак, имеющий форму прямоугольного параллелепипеда, объем которого V=a×b×h, где а, b, h - стороны бака.

Итак, мы подошли к задаче составления нашей первой модели. Прежде чем составить математическую модель, необходимо сформулировать содержательную постановку задачи, которая может быть следующей. Требуется определить размеры бака, объемом V = 2000, чтобы на его изготовление пошло как можно меньше материала, площадь которого равна S=2[a×b+(a+b)×h].

Такая постановка может быть записана следующим образом F=S_min

Эта запись читается так: минимизировать величину S при условии, что V = 2000. Подставим в формулу значения V и S, получим: F=2[a× b+(a+b)× h] 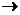min при ограничении a× b× h=2000.

К этим зависимостям добавим очевидное для нас, но необходимое для компьютера, условие, согласно которому все стороны прямоугольника могут быть только положительными величинами. Это условие запишем так: а, b, h > О,

Эта модель состоит из трех составляющих: целевой функции (ЦФ), ограничения (ОГР), граничных условий (ГРУ). Смысл этих составляющих рассмотрим чуть позже.

В эту систему, как и в нашу первую модель, входят три составляющие.

ЦФ - целевая функция или критерий оптимизации, показывает, в каком смысле решение должно быть оптимальным, т. е. наилучшим. При этом возможны 3 вида назначения целевой функции:

- максимизация;

- минимизация;

- назначение заданного значения.

ОГР - ограничения устанавливают зависимости между переменными. Они могут быть как односторонними, например

g_i < (x_j)<b_i,

так и двусторонними

а_i<g_i(x_j)< b_i,.

ГРУ - граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Решение задачи, удовлетворяющее всем ограничениям и граничным условиям, называется допустимым. Если математическая модель задачи оптимизации составлена правильно, то задача будет иметь целый ряд допустимых решений. Поясним это положение.

Важной характеристикой задачи оптимизации является ее размерность, определяемая числом переменных n и числом ограничений m. Соотношение этих величин является определяющим при постановке задачи оптимизации. Возможны три соотношения n < m, n = m, n > m, которые мы рассмотрим.

1. n < m - такие задачи решения не имеют.

2. n = m - такие задачи имеют одно решение

Для внимательного студента добавим, что когда мы говорим о количестве уравнений, то имеем в виду только линейно- независимые уравнения.

Напомним, что линейно-зависимыми называются такие уравнения, когда одно из них образуется умножением левой и правой части другого уравнения на постоянное число или сложением нескольких уравнений.

3. n > m - в этом случае может быть бесчисленное множество значений х₁ и х₂, которые удовлетворяют данному уравнению.

Таким образом, условие n > m - это непременное требование для задач оптимизации. Заметим, что такую систему уравнений, для которых n = m, можно рассматривать как задачу оптимизации, имеющую одно допустимое решение, и решать ее как обычную задачу оптимизации, назначая в качестве целевой функции любую переменную.

Итак, мы знаем, что система ограничений при n > m имеет бесчисленное множество решений. Принимающий решение должен абсолютно точно представлять, в чем заключается оптимальность решения, т. е. по какому критерию (от греч. kriterion - мерило, оценка, средство для суждения) принимаемое решение должно быть оптимально.

Критерий часто называют, и мы уже называли, целевой функцией. Критерий выбирается тем человеком, кто принимает решение. В общем случае с помощью критерия можно оценивать качества как желательные (например, прибыль, производительность, надежность), так и нежелательные (затраты, расход материала, простои оборудования). Тогда в первом случае стремятся к максимизации критерия, а во втором - к его минимизации.

Стремление к оптимизации - это естественное состояние человека. Человек по своей природе является прирожденным оптимизатором. Он занимается оптимизацией, потому что ему необходимо экономить свои ограниченные запасы энергии, ресурсов, времени. Каждый шаг человека, каждое принимаемое им решение - это зачастую неосознанное действие для того, чтобы получить оптимальный результат. И не случайно это естественное поведение человека нашло отражение в пословицах "Рыба ищет, где глубже, а человек - где лучше", что соответствует задаче максимизации, и "Из двух зол выбирают меньшее" - задаче минимизации.

Итак, задача имеет оптимальное решение, если она удовлетворяет двум требованиям:

- есть реальная возможность иметь более одного решения, т. е. существуют допустимые решения;

- имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т. е. наилучшим из допустимых.

3. Решение задачи на компьютере. Анализ результатов решения задачи. После того, как сформирована информационная знаковая модель, можно приступать собственно к компьютерному моделированию — созданию компьютерной модели и решению задач. Сразу возникает вопрос о средствах, которые необходимы для этого, т. е. об инструментах моделирования.

Существует бесчисленное множество программных комплексов, которые позволяют проводить исследование (моделирование) информационных моделей. Каждая программная среда имеет свой инструментарий и позволяет работать с определенными видами информационных объектов. Поэтому перед исследователем возникает нелегкий вопрос выбора наиболее удобной и эффективной среды для решения поставленной задачи.

Некоторые программные среды используются человеком как эффективное вспомогательное средство для реализации собственных замыслов. Иначе говоря, человек уже знает, какова будет модель, и использует компьютер для придания ей знаковой формы. Например, для построения геометрических моделей, схем используются графические среды, для словесных или табличных описаний — среда текстового редактора.

Другие программные среды используются как средство обработки исходной информации и получения и анализа результатов. Здесь компьютер выступает как интеллектуальный помощник. Так ведется обработка больших объемов информации в среде баз данных или проводятся вычисления в электронных таблицах.

В процессе разработки компьютерной модели исходная информационная знаковая модель будет претерпевать некоторые изменения по форме представления, т. к. должна ориентироваться на конкретную программную среду и инструментарий.

Например, если вы исследуете геометрическую модель, состоящую из элементарных графических объектов, для моделирования удобна среда графического редактора. Однако для разработки геометрических моделей в некоторых случаях может понадобиться среда программирования, обладающая графическими средствами.

Для словесных моделей используются текстовые процессоры с широкими возможностями оформления выходного документа — редактором формул, встроенной деловой графикой, элементами таблиц.

Существуют разнообразные программы, позволяющие включать в описание блок-схемы алгоритмов, электронные схемы, диаграммы и т. п.

При анализе объекта отталкиваются от общей формулировки задачи, четко выделяют моделируемый объект и его основные свойства. По сути, все эти факторы можно назвать входными параметрами моделирования. Их может быть довольно много, причем некоторые невозможно описать количественными соотношениями.

Очень часто исходный объект — это целая совокупность более мелких составляющих, находящихся в некоторой взаимосвязи. Слово «анализ» означает разложение, расчленение объекта с целью выявления составляющих, называемых элементарными объектами. В результате появляется совокупность более простых объектов. Они могут находиться между собой либо в равноправной связи,

Например, объект «комната» может быть представлен совокупностью более простых объектов — предметов мебели, расположенных в ней. Под моделированием будем понимать поиск наиболее удобной расстановки предметов мебели. Все они находятся в равноправной связи, т. е. могут занимать в комнате любое место.

Расположение объектов по степени подчиненности называется иерархией. Есть объекты и с более сложными взаимосвязями. Как правило, сложные объекты могут состоять из более простых с разными видами взаимосвязей.

В основу любой серьезной работы (будь то конструкторская разработка или проектирование технологического процесса, разработка алгоритма или моделирование) должен быть положен системный принцип «сверху вниз», т. е. от общих проблем к конкретным деталям. На этой идее основан и метод пошаговой детализации при создании алгоритмов, и модульный принцип организации программ и процесс управления государством, и процесс обучения детей в школе...