114=с14-(V4+U1)=1-(-4+0) =5;
124=с24-(V4+U2)=5-(-4+4)=5;
115=с15-(V5+U1)=0-(-6+0)=6;
125=с25-(V5+U2)=0-(-6+4)=2.
4. Производственно-транспортная задача. Выбор методов оптимизации планов перевозок. План не оптимален. Для его улучшения среди отрицательных значений lij берут клетку с наибольшим по абсолютной величине значением и строят из нее замкнутый контур или цепочку. В данном примере можно взять или клетку (2-1), или (3—2) (см. таблицу 7.3), в которой значения lij равны -5. Одна вершина контура должна лежать в этой свободной клетке, остальные — только в занятых клетках. Число вершин всегда должно быть четное. Контур, построенный из клетки (2—1), обозначен пунктиром. В вершине свободной клетки ставится знак (+), в остальных клетках знаки (+) и (—) чередуются.
В клетках с отрицательными вершинами выбирается наименьший объем перевозок, который вычитается из всех объемов перевозок по клеткам, имеющим отрицательные вершины контура, и прибавляется к объемам перевозок по клеткам с положительными вершинами контура. Отрицательные вершины контура расположены в клетках (1—1) с объемом перевозок, равным 100 т, и (2—2) — с объемом перевозок, равным 50 т. Следовательно, меньший объем перевозок в клетках с отрицательными вершинами контура равен 50. Этот объем вычитаем из клеток (1—1), (2—2), прибавляем к клеткам (2—1) и (1—2) и записываем в новую таблицу (таблицу 7.4).
Таблица 7.4 – 3-й опорный план
| Склад | Поле | Ресурсы | |||||
| Ui | -1 | ||||||
| -1 | |||||||
| Потребность в минераль-ных удоб-рениях |
|
|
Объем груза 50 т как бы переместился по контуру в свободную клетку (2-1) с наибольшей по абсолютному значению величиной. В новой таблице проверяется объем ограничений по строкам
Суммарные издержки на перевозку при таком плане равны:
Zmin=4*50+2*150+3*50+2*100+4*50+2*75+0*125=1200 тенге, или на 250 тенге меньше, чем в первоначальном плане.
Составленный план опять принимается за исходный, и вся вычислительная процедура повторяется снова. Приравняв U1 к нулю, рассчитывают все U1 и Vj для занятых клеток и записывают их в таблицу.
Затем проверяют план на оптимальность путем определения lij для свободных клеток:
131=с31-(V1+U3)=6-(4+1)=1;
122=с22-(V2+U2)=6-(2-1)=5;
132=с32-(V2+U3)=3-(2+1) =0;
113=с13-(V3+U1)=3-(3+0)=0;
114=с14-(V4+U1)=1-(1+0) =0;
124=с24-(V4+U2)=5-(1-1)=5;
115=с15-(V5+U1)=0-(-1+0)=1;
125=с25-(V5+U2)=0-(-1-1)=2.
Все значения lij для свободных клеток неотрицательны. Следовательно, план оптимален. Если бы имелись отрицательные значения lij, улучшение плана продолжалось бы уже разобранным способом.
По оптимальному плану на первое поле 50 т должны поступить с первого склада и 50 т—со второго. Потребности второго поля должны полностью удовлетворяться за счет первого склада. Для третьего поля 100 т должны поступить со второго склада и 50 т—с третьего. Кроме того, на третьем складе остаются неиспользованными 125 т минеральных удобрений, которые записаны по фиктивному полю.
При анализе оптимального плана видно, что не везде соблюдены минимальные издержки для отдельных полей. Так, для первого поля только половина потребности удовлетворена за счет наименьших издержек на перевозки—3 тенге за тонну. Вторая же половина потребности удовлетворена при более дорогих издержках—4 тенге за тонну. Для четвертого поля наиболее желательной перевозкой была бы перевозка с первого склада— по 1 тенге за тонну, однако его потребности полностью удовлетворены за счет третьего склада — по 2 тенге за тонну. Это оказалось выгодным с точки зрения общих затрат на перевозку удобрений. Следовательно, локальные оптимумы не всегда совпадают с общим оптимумом для всей задачи в целом.
|
|
Таблица 7.5 – 4-й опорный план
| Склад | Поле | Ресурсы | |||||
| Ui | -1 | ||||||
| -1 | |||||||
| Потребность в минераль-ных удоб-рениях |
Иногда, в оптимальном плане lij свободных клеток принимают нулевое значение. В этом случае нуль показывает, что имеется множество альтернативных решений, т.е. множество других планов перевозок, при котором общая сумма транспортных издержек не изменится.
В оптимальном плане данной задачи четыре свободные клетки имеют нулевые значения lij. Возьмем одну из них – клетку (1-3), построим для нее контур и сделаем изменения в плане по общему правилу (табл.). Получим новый план перевозок, у которого общая сумма транспортных затрат не изменилась (табл.).
Zmin=3*100+2*150+3*50+2*50+4*50+2*75 +0*125=1200.
Контрольные вопросы:
1. Как проверить план на оптимальность?
2. Какой план называется «вырожденным»?
3. Каким методом рассчитываются потенциалы занятых клеток?
4. Какая модель называется открытой, закрытой?
|
|
Лекция № 8
МОДЕЛИРОВАНИЕ АГРОИНЖЕНЕРНЫХ ПРОЦЕССОВ НА ОСНОВЕ ЭКОНОМИКО-СТАТИСТИЧЕСКИХ МОДЕЛЕЙ
1. Понятие и назначение производственных функций.
2. Виды и принципы классификаций производственных функций.
3. Построение производственных функций.
4. Определение параметров производственной функций и их анализ.
1. Понятие и назначение производственных функций. Объектом теории исследования операций являются большие организационно-управленческие системы (предприятия, объединения, фирмы, концерны, ведомства, министерства, системы распределения материальных, финансовых и трудовых ресурсов, системы текущего и перспективного планирования, научно-исследовательские институты, высшие уч. заведения и т.д.) Характерной особенностью этих систем является включение в них, наряду с материальными, денежными, энергетическими и информационными ресурсами, также и коллективов людей, взаимодействующих как между собой, так и с указанными ресурсами.
Под операцией будем понимать совокупность действий (мероприятий), направленных к достижению определенной цели. Цель операции – желаемое состояние объекта исследования после преобразования его совокупностью действий или желаемый результат деятельности.
Производственные функции являются моделями технологических зависимостей между результатами деятельности производственного объекта и затратами факторов производства. Выходные переменные – измеримые величины затрат живого труда, предметов и средств труда, используемых в процессе производства. Иногда переменными производственной функции являются не абсолютные, а относительные показатели, например, производительность труда, его фондовооруженность, показатели темпов роста и т.п.
Важнейшими показателями производственного процесса считают показатели выпуска продукции, используемых ресурсов, характеристики технологии и организации производства, а также показатели эффективности, которые определяются путем сопоставления показателей объема, структуры и качества выпуска с аналогичными показателями ресурсов. Это первичные характеристики производственного процесса.
Другую группу составляют приростные и темповые показатели динамики произв. процесса, которые вычисляются на основе показателей первой группы, например, абсолютный прирост выпуска продукции, прирост выпуска продукции на единицу основных фондов или на единицу приростачисленности работников, темп роста производительности труда или фондоотдачи и др.
Третья группа включает показатели, которые определяются по показателям второй группы, например, годовой прирост темпов роста производительности труда и т.п.
2. Виды и принципы классификаций производственных функций. Предприятия, фирмы имеют различные запасы: сырье, комплектующие изделия, готовую продукцию, предназначенную для продажи и т.п. Совокупность подобных материалов, представляющих временно не используемые экономические ресурсы, наз. запасами предприятия.
Запасы создаются по различным причинам. Одна из них состоит в том, что если в некоторый момент производства потребуется какой-то вид деталей, который поставляется другим предприятием, и он отсутствует на складе, то процесс производства может остановиться. Поэтому на складе должно быть всегда нужное количество деталей данного вида. Однако если запасы увеличить, то возрастет стоимость их хранения. Задача управления запасами состоит в выборе для предприятия целесообразного решения.
Рассмотрим простейшие математические модели управления запасами.
На рисунке 8.1 представлены возможные графики изменения запаса Q, имеющегося на складе, во времени t, для которого рассматривается этот запас.
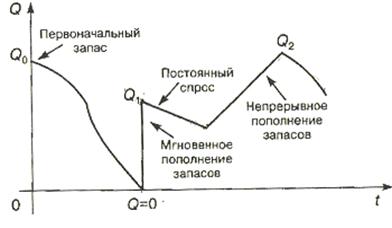
Рисунок 8.1 – Общая схема
Имеем первоначальный запас Qо. Видим, что линия опускается и значение Q падает. Предположим, что величина запаса непрерывна во времени. Если Q = 0, то имеет место дефицит.
Факторы, связанные с издержками:
Организационные издержки – расходы, связанные с оформлением и доставкой товаров, издержки содержания ресурсов – затраты, связанные с хранением. Они возникают при амортизации в процессе хранения (изделия могут портиться, устаревать, их количество может уменьшаться и т.д.).
Существуют издержки, связанные с дефицитом – если поставка сосклада не может быть выполнена, то возникают дополнительные издержки, связанные с отказом. Это может быть денежный штраф или ущерб, не осязаемый непосредственно, например, ухудшение бизнеса в будущем и потеря потребителей.
График изменения запасов представлен на рисунке 8.2.
Q
q
q/2 средний уровень запасов
0 0 0
Продолжитель-
ность цикла
Рисунок 8.2 – График изменения запасов
Как видно из рисунка, уровень запаса снижается равномерно от q до 0, после чего подается заказ на доставку новой партии величиной q. Интервал подачи называется циклом.
3. Построение производственных функций.. В основной модели предполагали, что поступление товаров на склад происходит мгновенно, например, в течение одного дня. Рассмотрим случай, когда готовые товары поступают на склад непосредственно с производственной линии. Будем считать, что поступление товаров происходит непрерывно. Модель задачи в этом случае называют моделью производственных поставок. Обозначим через p скорость поступающего на склад товара. Эта величина равна количеству товаров, выпускаемых производственной линией за год.
В течение времени t запас одновременно поступает и расходуется, это время накопления запаса, а t1 – запас только расходуется.
Модель запасов, включающая штрафы. Рассмотрим основную модель, допускающую возможность существования периодов дефицита, который покрывается при существующих поставках, и штрафов за несвоевременную поставку.
Предположим, что в начале каждого периода L предприятие делает запас, равный к. Это означает, что в течение перевозок будет наблюдаться дефицит товара и некоторое время поставки не будут осуществляться. Невыполненные заявки будут накапливаться до максимальной величины q-k и будут удовлетворены, как только поступит следующая партия товара в количестве q.
Кроме того, что товары доставляются предприятием позже необходимого срока, на предприятие налагается штраф, который зависит от того, насколько было задержана поставка.
График изменения запасов модели представлен на рисунке 8.3.
Интен
сивность
спроса g
q k A B
О C
период
дефицита
Рисунок 8.3 – Общая схема
(А-В)- выплачивается штраф.
(q-k)=y – максимальная величина задолженного спроса. При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем – пополняется запас.
Для определения оптимального значения к обозначим:
h - издержки хранения единицы товара за единицу времени,
p – затраты на штраф в расчете на единицу товара за один день отсрочки.
Найдем издержки одного цикла: С = С1+С2,
где С1 – общие издержки содержания запасов,
С2 – общие затраты на штраф.
Так как товары находятся на складе в течение периода ОА, средний уровень запасов за этот период равен к/2. Если продолжительность периода ОА равна k/g, то
С1= h*k/2 *k/g = hk2 /2g. (g – кол-во поставляемых товаров).
Так как штраф выплачивается в течение периода АВ=(q-k)/g, общее число «товаро-дней», на которые налагается штраф, равно площади треугольника АВС. Площадь составляет
(q-k)/g*(q-k)/2, откуда С2= p(q-k)2 /2 g.
Контрольные вопросы:
1. Раскройте сущность производственных функций и их значение в планово-экономической работе.
Лекция № 9
ЗАДАЧИ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ
1. Постановка задачи. Основные понятия и определения.
2. Классификация задач оптимального проектирования.
3. Методика получения исходных данных. Решение задач оптимального проектирования.
1. Постановка задачи. Основные понятия и определения. Под оптимальной структурой кормопроизводства в сельскохозяйственном предприятии понимается такое сочетание посевов кормовых культур на пашне, производства кормов на естественных угодьях, отходов товарных отраслей растениеводства и покупных кормов, которое обеспечит животноводство необходимыми кормами. При этом показатель, принятый в качестве критерия эффективности, достигает наилучшего значения.
Оптимальную структуру кормопроизводства можно рассчитать на основе экономико-математических моделей. Разработан ряд моделей, которые являются модификациями (частными случаями) общей модели оптимизации производственной структуры сельскохозяйственного предприятия.
Отличаются эти модели между собой следующим. В одних моделях задаются объемы производства животноводческой продукции, а критерием служат или минимум пашни, занятой кормовыми и зернофуражными культурами или минимум себестоимости кормов.
В других моделях в качестве критерия принимается максимум производства товарной, валовой продукции, чистого дохода и т. п.
Выбор критерия оказывает существенное влияние на оптимальную структуру кормопроизводства. Поэтому необходимо творчески подходить к его обоснованию в каждом конкретном случае. Критерий зависит от цели, которую ставит специалист при проведении оптимизационных расчетов.
В современных условиях функционирования хозяйственного механизма сельскохозяйственные предприятия в качестве критерия оптимальности в большинстве случаев принимают максимум прибыли.
Наиболее простая задача оптимизации структуры кормопроизводства возникает в случае, если сельскохозяйственное предприятие производит только один вид животноводческой продукции.
Поставим задачу рассчитать оптимальную структуру кормопроизводства для такого хозяйства с целью получения максимума прибыли.
2. Классификация задач оптимального проектирования. При построении экономико-математической модели будем использовать одну из классификаций расходов на производство (по связи с объемом производства), по которой все расходы подразделяются на две группы:
а) переменные или пропорциональные (изменяются в связи с изменением объема производства);
б) условно-постоянные или непропорциональные (остаются в основном на одном уровне независимо от объема производства).
При этом из переменных расходов выделим отдельно затраты на корма.
В оптимизационной модели можно использовать фактические значения тех показателей, которые в основном останутся неизменными и в оптимальном варианте, а именно: общая сумма условно-постоянных расходов; переменные расходы на 1 и продукции, затраты на производство 1 ц кормов каждого вида, стоимость покупных кормов.
3. Методика получения исходных данных. Для построения экономико-математической модели используются следующие исходные данные:
· площади кормовых угодий (пашни и естественных угодий);
· урожайности кормовых культур и естественных угодий;
· объемы побочной продукции товарных культур растениеводства;
· содержание кормовых единиц и перевариваемого протеина в кормах;
· материально-денежные затраты на 1 га кормов каждого вида;
· затраты на 1 ц побочной продукции товарных культур растениеводства;
· стоимость покупных кормов;
· общая сумма условно-постоянных расходов на производство животноводческой продукции (амортизация, текущий ремонт, общепроизводственные и общехозяйственные затраты);
· переменные затраты (без стоимости кормов) на 1 ц животноводческой продукции (зарплата с начислениями и прочие прямые затраты);
· продуктивность животных;
· затраты кормовых единиц и перевариваемого протеина на 1 ц (или голову животных) животноводческой продукции;
· структура затрат кормов на производство продукции животноводства;
· цена реализации 1 ц живого веса.
В экономико-математической модели в качестве искомых величин принимаются площади посевов кормовых и зернофуражных культур (отдельно по каждому виду корма), объемы побочной продукции товарных культур, используемые на корм, объем производства продукции животноводства (или поголовье животных) и некоторые другие показатели.
Контрольные вопросы:
1. Дайте классификацию задач оптимального проектирования.
2. Какие исходные данные используют для построения математических моделей?
Лекция № 10
МЕТОДИКА МОДЕЛИРОВАНИЯ ВЕРОЯТНОСТНЫХ ПРОЦЕССОВ
1. Моделирование как эксперимент. Метод Монте-Карло. Законы распределения случайных величин.
2. Формирование случайных величин с заданным законом распределения. Розыгрыш случайной величины по заданной гистограмме.
3. Реализация имитационных моделей на компьютере. Принципы оценки адекватности и точности имитационных моделей.
1. Моделирование как эксперимент. Экспериментальное исследование является необходимым этапом процесса познания. Имея дело с различными процессами и объектами в своей деятельности, человек постепенно накапливает практические сведения об этих процессах и объектах, что помогает ему познать их на основе этого знания усовершенствовать, оптимизировать. Зачастую таких сведений явно недостаточно, чтобы сделать какие-либо выводы. Тогда тот или иной объект, процесс подвергают планомерному экспериментальному исследованию.
Большинство исследований проводят для установления с помощью эксперимента функциональных или статистических связей между несколькими величинами или для решения экстремальных задач. Классический метод постановки эксперимента предусматривает фиксирование на принятых уровнях всех переменных факторов, кроме одного, значение которого определенным образом изменяют в области его существования. Этот метод составляет основу однофакторного эксперимента. При однофакторном эксперименте, варьируя один фактор и стабилизируя все прочие на выбранных уровнях, находят зависимость исследуемой величины только от одного фактора. Производя большое число однофакторных экспериментов при изучении многофакторной системы, получают частные зависимости, представленные многими графиками, имеющими иллюстративный характер. Найденные таким образом частные зависимости, невозможно объединить в одну общую. Отсюда следует, что результаты однофакторных экспериментов, полученные при исследовании многофакторных систем, часто малопригодны для практического использования.
Для изучения многофакторных систем наиболее целесообразным является применение статистических методов планирования эксперимента.
Только в конце 20-х годов ХХ в. Р.Фишер впервые показал целесообразность одновременного изменения нескольких (или всех) факторов в противовес широко распространенному классическому однофакторному эксперименту. В это время математическая статистика начинает делать первые шаги в изучении плохо организованных (сложных) систем, в которых отдельные явления не могут быть легко отделены одно от другого.
Примером сложной системы может служить почти любой технологический процесс. Здесь интуиция экспериментатора не может быть достаточно надежной опорой. В связи с этим становится чрезвычайно важным применение не только методов обработки, но и методов оптимальной организации (планирования) эксперимента.
Большой интерес к методам планирования эксперимента легко объясним: число опытов уменьшается в несколько раз; получается количественная оценка влияния факторов; находится подходящая математическая модель; определяются оптимальные условия протекания данного процесса и т.д.
В области с/х техники планирование эксперимента может сыграть исключительно важную роль на всех этапах ее создания и использования.
Несмотря на все трудности, связанные с пониманием того, что есть научный эксперимент, все же легко привести примеры как хорошо поставленных экспериментов, так и экспериментов в каком-то смысле явно плохих.
Для генерации случайных величин нужно иметь возможность получать последовательность равномерно распределенных случайных чисел, т.е. чисел, которые ведут себя как независимые реализации или выборки случайной величины R, равномерно распределенной на единичном интервале [0,1].
2. Метод Монте-Карло. Возникновение идеи использования случайных явлений в области приближённых вычислений принято относить к 1878 году, когда появилась работа Холла об определении числа p с помощью случайных бросаний иглы на разграфлённую параллельными линиями бумагу. Существо дела заключается в том, чтобы экспериментально воспроизвести событие, вероятность которого выражается через число p, и приближённо оценить эту вероятность. Отечественные работы по методу Монте-Карло появились в 1955-1956 годах. С того времени накопилась обширная библиография по методу Монте-Карло. Даже беглый просмотр названий работ позволяет сделать вывод о применимости метода Монте-Карло для решения прикладных задач из большого числа областей науки и техники.
Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались мало пригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию.
Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественностью получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятность.
, (10.1)
где Х – случайная величина,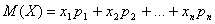 
- значения, вероятности которых соответственно равны 
.
Математическое ожидание приближённо равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания: 
.
Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии: 
.
Точечной называют оценку, которая определяется одним числом.
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок.
3. Законы распределения случайных величин. Нормальное распределение. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается дифференциальной функцией:
(10.2)
где а - математическое ожидание, s - среднее квадратичное отклонение нормального распределения.
Общая схема метода Монте-Карло. Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.
Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое 
и принимают x в качестве оценки (приближённого значения) a* искомого числа a:
(10.3)
Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.
Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) и по ним была найдена выборочная средняя 
, которая принята в качестве искомой оценки: 
. Ясно, что если повторить опыт, то будут получены другие возможные значения Х, следовательно, другая средняя, а значит, и другая оценка a*. Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы d допускаемой ошибки с заданной вероятностью (надёжностью) g: 
.