Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi+1-xi=h=const, т.е. xi=x0+ih, то интерполяционный полином можно записать в форме Ньютона. Первая интерполяционная формула Ньютона имеет вид
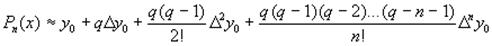
где 
, а выражения вида 
- конечные разности:
- разность первого порядка;
- разность второго порядка;
- разность k-го порядка.
Вторая интерполяционная формула Ньютона записывается в виде
где 
Интерполяционные полиномы в форме Ньютона удобно использовать если точка интерполирования находится вблизи начала (первая формула Ньютона) или конца таблицы (вторая формула Ньютона). Эти полиномы интересны тем, что каждая частичная сумма первых m слагаемых есть интерполяционный полином m-1 степени, построенный по m первым (для первой формулы) или последним (для второй формулы) табличным точкам. Поэтому интерполяционные полиномы Ньютона удобно использовать при последовательном увеличении степени интерполяционного многочлена.
Пусть, например, для вычисления значения f(x) некоторой точке x вычислен полином Pn(x) по n+1 точкам x0,x1,...xn, а затем для уточнения этого значения привлечен еще один узел xn+1, тогда для вычисления Pn+1(x) по n+2узлам с помощью формулы Лагранжа нужно заново пересчитывать все слагаемые, а в первой формуле Ньютона требуется вычислить только одно слагаемое
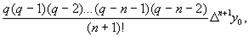по величине которого можно, кстати, определить и целесообразность дальнейшего увеличения степени интерполяции.
Ошибка приближения функции интерполяционным полиномом это разность Rn(x)=f(x)-Pn(x). можно получить следующие выражения для погрешности интерполяции:
для первой формулы Ньютона
для второй формулы Ньютона
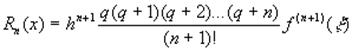
где - некоторая точка интервала [x0,xn] или [x-n,xn].
ПРИМЕР. Дана таблица значений теплоёмкости вещества в зависимости от температуры Cр =f(T).
Таблица 5.3
| x (T) | ||||
| Y (Cp) | 52.88 | 65.61 | 78.07 | 99.24 |
Построить интерполяционный многочлен Ньютона для заданных значений функции. n=3; h=100.
Составим таблицу конечных разностей функции.
| x | y |  y
| 2 y
| 3 y
|
| 52.88 | 12.73 | -0.27 | 8.98 | |
| 65.61 | 12.46 | 8.71 | ||
| 78.07 | 21.17 | |||
| 99.24 |
После выполнения преобразований получим интерполяционный многочлен вида:
Полином имеет третью степень и дает возможность вычисления при помощи найденной формулы значения y для неизвестного x.
Если для описания табличных данных будет выбрана функция с меньшим количеством коэффициентов (m < n), что часто встречается на практике, то уже нельзя подобрать коэффициенты функции так, чтобы функция проходила через каждую узловую точку. В лучшем случае она будет проходить каким - либо образом между ними и очень близко к ним. Такой способ описания табличных данных называется аппроксимацией, а функция - аппроксимирующей.
Если аналитическое выражение функции f(x) неизвестно или весьма сложно, то возникает практически важная задача: найти такую эмпирическую формулу
 ,
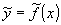| (5.22) |
значения которой при x=xi возможно мало отличались бы от опытных данных yi (i=1, 2, …, n).