Рассмотрим систему линейных алгебраических уравнений
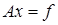, (42)
где А - матрица размерности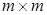 
, 
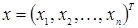- вектор решения, 
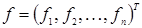- вектор правых частей.
Численные методы решения данной системы принято разделять на два класса: прямые методы («точные») и итерационные.
Прямыми методами называются методы, позволяющие получить решение системы уравнений (42) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Суть итерационных методов состоит в том, что решение системы (42) находится как предел последовательных приближений x(n) при n®¥, где n - номер итерации. При использовании методов итерации обычно задается некоторое малое число e>0 и вычисления проводятся до тех пор, пока не будет выполнена оценка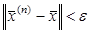 
. К этим методам относятся метод Зейделя, Якоби (метод простых итераций), метод верхних релаксаций и т.д.
Число итераций n = n (e), которое необходимо выполнить для получения заданной точности e, является основной оценкой качества метода. По этому числу проводится сравнение различных методов.
Итерационные методы также делятся на одношаговые, когда для определения решения на j +1 итерации используются значения решения, найденные на j итерации, и многошаговые, когда для определения решения на j +1 итерации используется несколько предыдущих итераций.
Наиболее популярные численные методы решения систем уравнений: метод простых итераций, метод Зейделя (используются для решения как систем линейных, так и нелинейных уравнений), различные модификации метода Гаусса (для решения систем линейных уравнений), метод Ньютона (для решения систем нелинейных уравнений).
Метод Гаусса. Запишем систему Ax=f, в развернутом виде
|
|
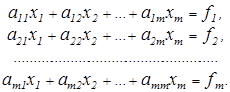
Следует отметить, что рассматривается квадратная матрица А и ее определитель не равен 0 det A≠0/
Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что 
. Последовательно умножая первое уравнение на 
и складывая с i -м уравнение, исключим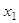 
из всех уравнений кроме первого. Получим систему
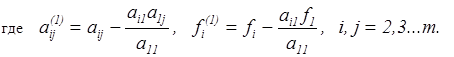
Аналогичным образом из полученной системы исключим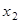 
. Последовательно, исключая все неизвестные, получим систему треугольного вида
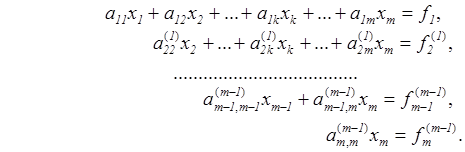
Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все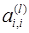 
, 
не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
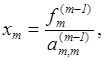
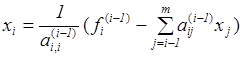.Эта процедура получила название обратный ход метода Гаусса.
Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность.
Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду позволяют вычислить определитель матрицы
.
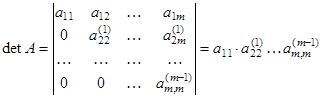Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение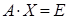 
,
где Е - единичная матрица. Его решение сводится к решению m систем
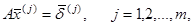
у вектора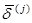 
j –я компонента равна единице, а остальные компоненты равны нулю.