Численное дифференцирование используется для приближенного вычисления производных функции заданной таблицей и для функций, которые по разным причинам неудобно или невозможно дифференцировать аналитически. В последнем случае вычисляется таблица функции в окрестности исследуемой точки и по этим значениям вычисляется приближенное значение производной.
Итак, пусть в точках xi, i=0,1,2,...n известны значения функции yi=f(xi). Способ построения формул численного дифференцирования состоит в том, что по табличным точкам строится интерполяционный полином Pn(x) который дифференцируется нужное число раз и делается допущение о том, что производная от функции приблизительна равна производной от интерполяционного полинома.
Погрешность такой формулы характеризуется k-той производной от ошибки интерполяции 
.
При кусочно-линейной интерполяции по равноотстоящим узлам xi=x0+i h
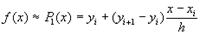
получим очевидную формулу для x 
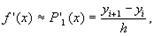(1)
либо, если использовать интерполяцию вида
для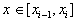 
получим
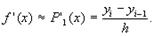(2)
Формулы (1) и (2) называются правым разностным соотношением и левым разностным соотношением, их можно было бы записать сразу используя определение производной и не привлекая интерполяцию как промежуточный этап. Однако для получения более точных формул и для вычисления производных высших порядков без интерполирования не обойтись.
Дифференцируя интерполяционный многочлен в виде первой формулы Ньютона получим
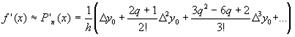(3)
где q= (x-x0) /h
Такая форма записи позволяет последовательно получать формулы дифференцирования различной степени точности, но для практических вычислений более удобна форма содержащая не конечные разности, а значения функции в табличных точках. Так при квадратичной интерполяции для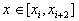 
получим
|
|
(4)
Если требуется вычислить производную в одной из табличных точек, то формулы упрощаются. В частности, для x=xi по формуле (4) получим
. Это так называемое центральное разностное отношение.
При x=x0 из (4) получим выражение
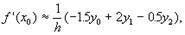
а при кубической интерполяции получаем
Формулы для вычисления производных второго порядка получаются путем повторного дифференцирования интерполяционного полинома. Например, дифференцируя (3) еще раз и подставляя x=x0 получим
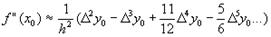
При использовании значений функции вместо конечных разностей для квадратичной интерполяции получим формулу
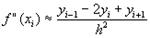
При численном дифференцировании возникает методическая ошибка, вызванная заменой функции f(x) интерполяционным многочленом Pn(x), и ошибка округления, вызванная неточным заданием значений функции в табличных точках. Методическая погрешность оценивается производной от ошибки интерполирования 
и при уменьшении шага, как правило, уменьшается. В частности для формулы (1) величина методической погрешности оценивается соотношением
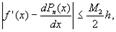,где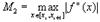 
Погрешность округления для всех случаев оценивается величиной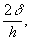 
где б -абсолютная погрешность исходных значений f(xi).
Таким образом, методическая погрешность при уменьшении шага интерполирования уменьшается, а погрешность округления обратно пропорциональна шагу и при уменьшении шага может как угодно сильно исказить получаемый результат, т.е. численное дифференцирование неустойчиво. Исходя из этого шаг следует выбирать таким, чтобы суммарная погрешность была минимальна.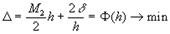 
|
|
В ряде случаев наряду с приближенным равенством удается (например, используя формулу Тейлора) получить точное равенство, содержащее остаточный член R (погрешность численного дифференцирования):
f(r)(x) = P(r)N(x) + R, 0 ≤ r ≤ N
Такие формулы называются формулами численного дифференцирования с остаточными членами. Степень, с которой входит величина в остаточный член, называется порядком погрешности формулы численного дифференцирования. Формулы с отброшенными остаточными членами называются просто формулами численного дифференцирования.
Остаточные члены этих формул находятся с помощью формулы Тейлора. При этом предполагается, что на отрезке [ x0, xN ] у функции f(x) непрерывна производная, через которую выражается остаточный член. При четном N в среднем узле для четной производной порядок точности формулы на единицу больше, чем в остальных узлах. Поэтому рекомендуется по возможности использовать формулы численного дифференцирования с узлами, расположенными симметрично относительно той точки, в которой ищется производная.
Рассмотрим разложения в ряд Тейлора
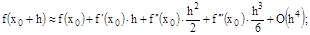(1)
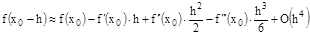. (2)
Здесь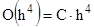 
– величина порядка 
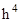(С – некоторая постоянная). Из (1) найдем
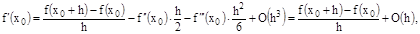(3)
где 
– величина порядка h.
Другой способ построения формул численного дифференцирования приводит к тем же формулам - метод неопределённых коэффициентов. Чаще всего метод используется в многомерном случае, когда построить интерполяционный многочлен достаточно сложно. В этом случае коэффициенты численного дифференцирования ci выбираются из того, чтобы формула 
была точна для многочленов максимально высокой степени. Пусть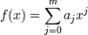 
и потребуем, чтобы для такого многочлена соотношение для f(k)(x) обратилось в равенство: 
. Чтобы равенство выполнялось для любого многочлена степени m, необходимо и достаточно, чтобы коэффициенты при aj в правой и левой частях были равны (xj)(k) = j(j − 1)...(j − k + 1)xj − k. Получаем систему уравнений: 
относительно ci. Если m = n − 1, то число уравнений равно числу неизвестных. Определитель системы (определитель Вандермонда)отличен от нуля, то есть всегда можно построить формулу численного дифференцирования с n узлами, точную для многочленов степени n − i.
|
|
Пример
Вычислить точное и приближенное значения производной функции y=x*x в точке x=1 с шагом h=1 и h=0.001.
Аналитическое решение: y'=2x, y'(1)=2
Численное решение для шага: h=1
,
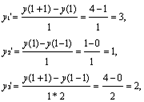для шага h=0.001
