Классический метод для функции одной переменной
На рис. 1.1 дано графическое представление функции f(x), которая имеет локальный минимум в точке 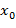 и глобальный минимум в точке
и глобальный минимум в точке  .
.
Классический подход к задаче нахождения значений 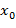 и
и  состоит в поиске уравнений, которым они должны удовлетворять. Представленная на рис. 1.1 функция и ее производные непрерывны, и видно, что в точках
состоит в поиске уравнений, которым они должны удовлетворять. Представленная на рис. 1.1 функция и ее производные непрерывны, и видно, что в точках  и
и 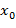 производная
производная  (градиент функции) равна нулю. Следовательно,
(градиент функции) равна нулю. Следовательно,  и
и 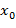 будут решениями уравнения
будут решениями уравнения 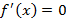 . (1.1)
. (1.1)
Точка  , в которой достигается локальный максимум, и точка
, в которой достигается локальный максимум, и точка 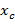 , в которой имеется точка горизонтального перегиба функции, также удовлетворяют этому уравнению. Следовательно, уравнение
, в которой имеется точка горизонтального перегиба функции, также удовлетворяют этому уравнению. Следовательно, уравнение 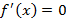 является только необходимым условием минимума, но не является достаточным условием минимума.
является только необходимым условием минимума, но не является достаточным условием минимума.
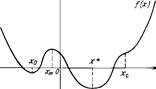
Рис. 1.1
Заметим, однако, что в точках  и
и 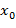 производная
производная 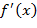 меняет знак с отрицательного на положительный. В точке
меняет знак с отрицательного на положительный. В точке  знак меняется с положительного на отрицательный, в то время как в точке
знак меняется с положительного на отрицательный, в то время как в точке 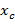 он не меняется. Следовательно, производная в минимуме является возрастающей функцией, а поскольку степень возрастания
он не меняется. Следовательно, производная в минимуме является возрастающей функцией, а поскольку степень возрастания 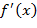 измеряется второй производной, можно ожидать, что
измеряется второй производной, можно ожидать, что 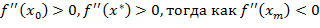 .
.
Если, однако, вторая производная равна нулю, ситуация остается неопределенной.
Полученные выше результаты могут найти надежное обоснование, если рассмотреть разложение функции f(x) в ряд Тейлора в окрестности точки 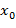 (или
(или  , или
, или  ), что, конечно, требует непрерывности функции f(x) и ее производных:
), что, конечно, требует непрерывности функции f(x) и ее производных:
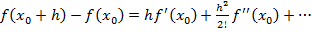 (1.2)
(1.2)
Если в точке 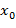 достигается минимум, то левая часть (1.2) будет неотрицательной для любого достаточно малого h (
достигается минимум, то левая часть (1.2) будет неотрицательной для любого достаточно малого h ( ). Следовательно, первая производная
). Следовательно, первая производная 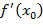 должна быть равна нулю, и это является достаточным условием (см. уравнение (1.1)). Если бы она была положительной, то достаточно малое отрицательное значение h делало бы правую часть (1.2) отрицательной, а если бы она была отрицательной, то достаточно малое положительное значение h делало бы правую часть отрицательной.
должна быть равна нулю, и это является достаточным условием (см. уравнение (1.1)). Если бы она была положительной, то достаточно малое отрицательное значение h делало бы правую часть (1.2) отрицательной, а если бы она была отрицательной, то достаточно малое положительное значение h делало бы правую часть отрицательной.
Так как в следующем члене (1.2) всегда 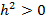 , то, если
, то, если 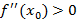 , в точке
, в точке 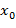 достигается минимум. Если
достигается минимум. Если 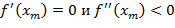 , то из аналогичных соображений в точке
, то из аналогичных соображений в точке  достигается максимум. Для определения различия между локальным и глобальным минимумами необходимо сравнить значения функций
достигается максимум. Для определения различия между локальным и глобальным минимумами необходимо сравнить значения функций 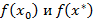 .
.
Пример:
Исследовать характер точек перегиба 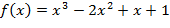
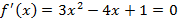
Тогда х = 1/3 или 1.
При x=1/3 производная 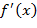 меняет знак с + на -, а при x=1 c – на +. Следовательно, в точке 1/3 максимум, в точке 1 минимум.
меняет знак с + на -, а при x=1 c – на +. Следовательно, в точке 1/3 максимум, в точке 1 минимум.
Этот пример может быть решен более простым способом, если вычислить вторую производную 
 ,, т. е. отрицательна, и при x = 1/3 достигается максимум;
,, т. е. отрицательна, и при x = 1/3 достигается максимум;
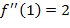 , т. е. положительна, и при х = 1 достигается минимум.
, т. е. положительна, и при х = 1 достигается минимум.
Неоднозначность, возникающую при f"(x) = 0, можно разрешить, увеличив количество членов в формуле разложения в ряд Тейлора:
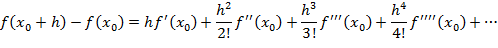
При этом можно сформулировать следующее правило:
Если функция f(х) и ее производные непрерывны, то точка 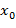 является точкой экстремума (максимума или минимума) тогда, и только тогда, когда n четное, где n — порядок первой необращающейся в нуль в точке
является точкой экстремума (максимума или минимума) тогда, и только тогда, когда n четное, где n — порядок первой необращающейся в нуль в точке 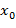 производной. Если
производной. Если 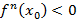 , то в точке
, то в точке 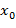 достигается максимум, если
достигается максимум, если 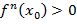 , то в точке
, то в точке 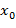 достигается минимум.
достигается минимум.