Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент 
равнялся единице (так удобнее производить преобразования матрицы).
.
Имеем 
Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно.
Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: 
Итак, имеем 
Далее, подставляя 
в третье уравнение, найдем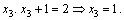 
Подставляя 
и 
во второе уравнение, получим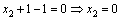 
и, наконец, подставляя в первое уравнение найденные 
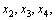получим 
Таким образом, имеем решение системы 
LU–метод. LU-метод основан на том, что если главные миноры матрицы А отличны от нуля, тогда матрицу А можно представить, причем единственным образом, в виде произведения
А=LU, где L–нижняя треугольная матрица с ненулевыми диагональными элементами и U–верхняя треугольная матрица с единичной диагональю.
Рассмотрим СЛАУ Ax=f.
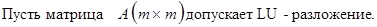A=LU где
или
, 
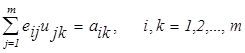Окончательно запишем
, 
Полагая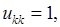 
получим следующие рекуррентные формулы для вычисления элементов матрицы L и U
Если найдены матрицы L и U, то решение исходной системы (1)ID_1 сводится к последовательному решению двух систем уравнений с треугольными матрицами
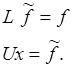
Введя вектор вспомогательных переменных y, последнее выражение можно переписать в виде системы
|
Таким образом, решение данной системы с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.
Очевидно, все y i могут быть найдены из системы Ly = b при i =1, 2,…, N по формуле (прямой ход)
| (1.6) |
Значения неизвестных x i находятся из системы Ux = y в обратном порядке, т.е. при i = N, N –1,…, 1, по формуле (обратный ход)
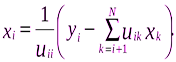
| (1.7) |
LU – метод позволяет вычислить определитель матрицы А
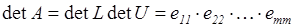. Вычислительная сложность данного метода порядка n3
Итерационные методы.
Метод простой итерации (Якоби). Для применения метода простой итерации к системе линейных алгебраических уравнений 
с квадратной невырожденной матрицей А, необходимо предварительно преобразовать эту систему к виду 
. (*)
Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и зависит от специфики системы. Самый простой способ приведения системы к удобному виду -
.
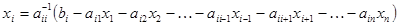Получаемая в результате матрица, где 
и 
(Разрешим каждое из уравнений (1) относительно неизвестного в главной диагонали, т.е. из первого уравнения выразим x1, из второго x2 и т.д.). В таком виде метод простой итерации называют методом Якоби.
Описание метода. Выберем начальное приближение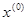 
. Подставляя его в правую часть системы, вычисляем первое приближение 
. Т.о. получаем последовательность приближений, вычисляемых по формуле
.
За нулевое приближение часто принимают столбец свободных членов. Если последовательность приближений 
имеет предел 
Достаточное условие сходимости процесса итерации сформулированы в теореме:
Если для приближенной системы выполнено, по меньшей мере, одно из условий
1) 
или
2) 
то процесс итерации сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие: Для системы
метод итерации сходится, если выполнены неравенства
т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов). То сходимость процесса итерации зависит только от свойств матрицы a. Под нормой матрицы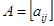 
понимается действительное число 
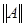, удовлетворяющее условиям:
а) 
; причем 
, тогда только тогда, когда A= 0;
б)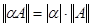 
(a - число), в частности 
в)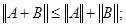 
г) 
Норма называется канонической, если дополнительно выполнены условия:
д) если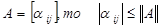 
причем для скалярной матрицы 
е) из неравенства 
следует неравенство 
A и B – матрицы
Достаточное условие сходимости процесса итерации можно сформулировать, используя понятие нормы матрицы:
Процесс итерации для приведенной линейной системы 
. Сходится к единственному её решению, если какая-нибудь каноническая норма матрицы 
. (
- произвольно).
Следствие: процесс итерации для приведенной линейной системы сходится, если
а) 
или
б) 
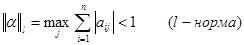или
в)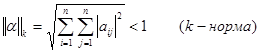 
В частности, процесс итерации заведомо сходится, если элементы матрицы a удовлетворяют неравенству 
, где n – число неизвестных в системе.
Метод Зейделя. Этот метод можно рассматривать как модификацию метода Якоби. Идея заключается в том, что при нахождении очередного (k+1) приближения неизвестного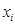 
используют уже известные приближения x1,x2,...xi-1, а не k-е приближения.
Пусть дана приведенная линейная система 
Выберем произвольно начальное приближение корней 
стараясь, конечно, чтобы они в какой-то мере соответствовали искомым неизвестным 
. Предполагая, что k-ое приближение корней 
известны, согласно методу Гаусса-Зейделя будем строить (k+1)-е приближение корней по следующим формулам:
(5.17)
Заметим, что теорема сходимости для простой итерации остается верной для итерации по методу Гаусса-Зейделя.
Постановка задачи для нелинейной системы уравнений: Найти такие действительные числа 
, что все уравнения системы
(1.1)
одновременно обращаются в тождества. Другая форма записи системы (1.1):
, i = 1,2,..., n. (1.2)
Соотношения (1.1) - (1.2) - это запись системы уравнений в нормальном виде.
Порядок применения методов простых итераций и Зейделя
Исходная система преобразуется к эквивалентному виду: 
, i = 1,2,..., n (из одного уравнения выражается 
, из другого –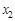 
и т.д.). Выбираются начальные значения неизвестных: 
, i =1,2,..., n и реализуется итерационный процесс вычисления приближений к решению системы по правилам:
метод простых итераций - 
, k =0,1,2,...; i =1,2,..., n;
метод Зейделя - 
, k =0,1,2,...; i =1,2,..., n.
Условие прекращения процесса:
для систем нелинейных уравнений – 
< e (1.4)
(e- заданная точность решения), при этом 
, i = 1,2,..., n.
Достаточное условие сходимости итерационных процессов:
1) функции 
, i =1,2,..., n определены и непрерывно дифференцируемы в некоторой окрестности решения системы;
2) начальное 
и все вычисляемые приближения к решению системы находятся в этой окрестности;
3) во всех точках окрестности одновременно выполняются неравенства
, i =1,2,..., n. (1.5)
В вычислительной практике методы простых итераций и Зейделя применяются для решения систем нелинейных уравнений сравнительно редко – когда порядок системы не превышает 3. С увеличением порядка становится все сложнее проверять условие сходимости итераций, т.е. формировать и решать систему нелинейных неравенств (1.5). Гораздо чаще эти методы применяют для решения систем линейных уравнений:
Метод Ньютона. Метод Ньютона - наиболее популярный численный метод решения систем нелинейных уравнений. Он предусматривает выделение из уравнений системы линейных частей, которые играют определяющую роль при малых приращениях аргументов. В результате решение системы нелинейных уравнений сводится к решению последовательности систем линейных уравнений.
Обозначим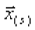 
некоторое приближение к корню системы уравнений 
. Пусть малое 
. Вблизи 
каждое уравнение системы можно линеаризовать следующим образом:
, 1 ≤ k ≤ n. (2)
Это можно интерпретировать как первые два члена разложения функции в ряд Тейлора вблизи 
. Тогда система примет вид:
, 1 ≤ k ≤ n. (3)
Мы получили систему линейных уравнений, неизвестными в которой выступают величины 
. Решив ее, например, методом Гаусса, мы получим некое новое приближение к 
, т.е. 
. Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона:
, (4)
где в данном случае
– матрица Якоби, которая считается для каждого (s) приближения.
Критерием окончания итерационного процесса является условие 
(Можем принять под 
как норму 
, так и 
). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если 
, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.