Обыкновенным дифференциальным уравнением называется выражение
 , где x – независимая переменная; y – искомая функция от x;
, где x – независимая переменная; y – искомая функция от x;  - производные соответственного порядка.
- производные соответственного порядка.
Уравнение называется разрешенным относительно старшей производной, если имеет вид: y (n) = f (x, y, y ',..., y (n − 1)).
Уравнение, разрешенное относительно старшей производной, сводится к системе n обыкновенных дифференциальных уравнений первого порядка с помощью замены y 1 = y ', y 2 = y '',..., yn − 1 = yn − 1, что дает:
 ,
,
 ,
,
...
 ,
,
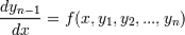 .
.
Задача Коши для дифференциального уравнения n-ого порядка
y (n) = f (x, y, y ',..., y (n − 1)) заключается в отыскании функции y=y(x), удовлетворяющей этому уравнению и начальным условиям  , где
, где  - заданные числа.
- заданные числа.
Задача Коши для системы дифференциальных уравнений

заключается в отыскании функций y 1, y 2,..., yn, удовлетворяющих этой системе и начальным условиям y 1(x 0) = y 10, y 2(x 0) = y 20,..., yn (x 0) = yn 0.
Если удается найти общее решение уравнения или системы, то задача Коши сводится к отысканию значений произвольных постоянных. Но найти общее решение задачи Коши удается в редких случаях; чаще всего приходится решать задачу Коши приближенно.
Для приближенных вычислений существует несколько численных методов, как то: метод последовательных приближений, метод Эйлера, метод Рунге-Кутта, метод Милна и др.
Метод Эйлера. Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

где yi+1 это искомое значение функции в точке xi+1.
Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить yi+1, если известно yi в точке хi:
 (6.4)
(6.4)
Графическая интерпретация метода Эйлера также не представляет затруднений (см. рисунок ниже). Действительно, исходя из вида решаемого уравнения) следует, что значение  есть значение производной функции y(x) в точке x=xi -
есть значение производной функции y(x) в точке x=xi -  , и, таким образом, равно тангенсу угла наклона касательной, проведенной к графику функции y(x) в точке x=xi.
, и, таким образом, равно тангенсу угла наклона касательной, проведенной к графику функции y(x) в точке x=xi.
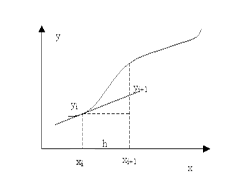
Из прямоугольного треугольника на рисунке можно найти
 ,откуда и получается формула Эйлера. Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=xi. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:
,откуда и получается формула Эйлера. Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=xi. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:
Процесс вычислений строится следующим образом. При заданных начальных условиях x0 и y0 можно вычислить таблицу значений функции y(x) с определенным шагом (h) по x на отрезке [x0, xN]. Ошибка в определении значения y(xi) при этом будет тем меньше, чем меньше выбрана длина шага h (что определяется точностью формулы интегрирования). Шаг интегрирования h берется меньше шага сетки, на которой определяется решение.
Для погрешности метода Эйлера на одном шаге справедлива оценка

а для оценки погрешности решения на всём отрезке [ a, b ] справедливо

Для практической оценки погрешности можно рекомендовать правило Рунге: производятся вычисления с шагом h — вычисляются значения y ( h ) i, затем производятся вычисления с половинным шагом h /2 — вычисляются значения y ( h /2) i. За оценку погрешности вычислений с шагом h /2 принимают величину 
Если соединить точки (xi, yi) прямолинейными отрезками, получим ломаную Эйлера — ломаную линию, каждое звено которой с началом в точке (xi, yi) имеет угловой коэффициент, равный f (xi, yi).
Пример. Решим задачу Коши
y ' = y 2 − x, y (1) = 0 на отрезке [1, 3] методом Эйлера с шагом h = 0.2 и с шагом h = 0.1.
Изобразим решение графически. Оценим погрешность.
Вычисления с шагом h = 0.2:
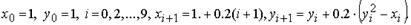
Ниже приведены: таблица значений приближённого решения в узлах равномерной сетки с шагом h = 0.2, график приближённого решения и ломаная Эйлера.

Метод Рунге-Кутта. Метод Рунге-Кутта основан на использовании для вычисления интегралов 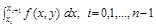 формулы Симпсона:
формулы Симпсона:
 .
.
Определив значения 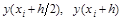 по методу Эйлера, получим
по методу Эйлера, получим
 i =0,1,…, n.
i =0,1,…, n.
Это формула метода Рунге-Кутта 3-го порядка. На практике чаще используется метод Рунге-Кутта 4-го порядка:
 (1.32)
(1.32)
где 
 Ошибка формулы (1.32) пропорциональна h 5.
Ошибка формулы (1.32) пропорциональна h 5.
Этот метод намного более точен, чем методы Эйлера, но требует и большего объема вычислений: положение точки (xi +1, yi +1) определяется в результате 4-кратного вычисления значения функции f (x, y). С появлением ЭВМ этот недостаток перестал быть существенным и метод Рунге-Кутта 4-го порядка применяется на практике чрезвычайно широко.
Пример. Используя алгоритм Рунге-Кутты третьего и четвертого порядков решить задачу с шагом h =0.1:
 На сетке с шагом 0,1 в интервале [0, 1]
На сетке с шагом 0,1 в интервале [0, 1]
Решение:
Для алгоритма третьего порядка (для узла x=0.1) вычисления таковы:



Для алгоритма четвертого порядка (для узла x=0.1) вычисления таковы:




В качестве примера удобно брать дифференциальное уравнение вида: y' = y (для него известно точное решение y = ex) с простейшим начальным условием y(0) = 1, и решать итерационно методом Рунге-Кутта.
Краевая задача. Если дополнительные условия задаются более чем в одной точке, т.е. при разных значения независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются при этом граничными (или краевыми) условиями. На практике, обычно граничные условия задаются в двух точках  и
и  , являющихся границами отрезка, на котором рассматривается решение дифференциального уравнения. Минимальный порядок ОДУ, для которого может быть сформулирована краевая задача, равен двум.
, являющихся границами отрезка, на котором рассматривается решение дифференциального уравнения. Минимальный порядок ОДУ, для которого может быть сформулирована краевая задача, равен двум.
Ниже приведен пример ОДУ второго порядка с граничными условиями (заданы значения функции в двух различных точках):

Метод прогонки (Конечно-разностный метод). Пусть на отрезке  требуется найти решение дифференциального уравнения
требуется найти решение дифференциального уравнения
 8.1 удовлетворяющее следующим краевым условиям:
8.1 удовлетворяющее следующим краевым условиям: 


 8.2
8.2
Численное решение задачи состоит в нахождении приближённых значений  искомого решения
искомого решения  в точках
в точках  . Точки
. Точки  называются узлами сетки. Используем равномерную сетку, образованную системой равноотстоящих узлов
называются узлами сетки. Используем равномерную сетку, образованную системой равноотстоящих узлов 
 . При этом
. При этом  ,
,  ,
,  . Величина
. Величина  – шаг сетки. Пусть
– шаг сетки. Пусть  ,
, 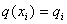 ,
,  ,
,  ,
,  ,
,  . Аппроксимируем
. Аппроксимируем  и
и  в каждом внутреннем узле центральными разностными производными
в каждом внутреннем узле центральными разностными производными
 ,
, 
и на концах отрезка – односторонними производными
 ,
, 
Используя эти формулы, получаем разностную аппроксимацию исходной задачи (8.1) – (8.2):
 (8.3)
(8.3)
Чтобы найти приближённые значения  искомого решения, необходимо решить систему
искомого решения, необходимо решить систему  линейных уравнений (8.3) с
линейных уравнений (8.3) с  неизвестными. Эту систему можно решить одним из стандартных методов решения линейных систем. Однако матрица системы (8.3) трёхдиагональная, поэтому для её решения применим специальный метод, называемый методом прогонки.
неизвестными. Эту систему можно решить одним из стандартных методов решения линейных систем. Однако матрица системы (8.3) трёхдиагональная, поэтому для её решения применим специальный метод, называемый методом прогонки.
Перепишем систему (3) следующим образом:

 (8.4)
(8.4)
где  ,
,  ,
,  ,
, 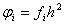 ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
,  .
.
Будем искать решение системы в виде  .(
.( ) Подставляя это выражение в (8.4) получаем что
) Подставляя это выражение в (8.4) получаем что  ,
, 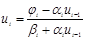 где
где  ,
,  . Вычисляем
. Вычисляем  ,
,  . (Прямой ход прогонки). Обратный ход подразумевает вычисление
. (Прямой ход прогонки). Обратный ход подразумевает вычисление  в обратном порядке
в обратном порядке 

