Нормативная скорость ветра максимальной интенсивности

 

Ветровые районы России	I	II	III	IV	V	VI	VII
Нормативная скорость ветра v„, м/с		25.

Таблица 9

Аэродинамический коэффициент лобового сопротивления

провода ветру С_х для различных проводов, в том числе

Покрытых гололедом

 

Провода	Коэффициент
Одиночные провода и тросы диаметром 20 мм	1,2
Одиночные контактные провода и несущие тросы контактной подвески с учетом зажимов и струн	1,25
Одиночные овальные контактные провода	1,15
Одиночные контактные провода сечением 150 мм2	1,30
Двойные контактные провода при расстоянии между ними 40 мм	1,85

Результирующая (суммарная) нагрузка на несущий трос в даН/м в режиме максимального ветра определяется по формуле:

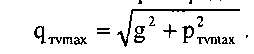(5)

При определении результирующей нагрузки на несущий трос ветровая нагрузка на контактные провода не учитывается, т.к. она в основном воспринимается фиксаторами.

2.3. В режиме гололеда с ветром на несущий трос действуют вертикальные нагрузки от собственного веса проводов контактной подвески, от веса гололеда на проводах подвески и горизонтальная нагрузка от давления ветра на несущий трос, покрытый гололедом при скорости ветра v_r; t_x = t_r = -5°С.

Вертикальная нагрузка от собственного веса 1 м проводов подвески определена выше по формуле (3).

Вертикальная нагрузка от веса гололеда на несущем тросе в даН/м определяется по формуле:

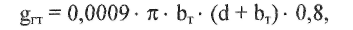(6)

 

где Ь_т - толщина стенки гололеда на несущем тросе, мм; d - диаметр несущего троса, мм; 71 = 3,14. Толщина стенки гололеда на несущем тросе Ь_т в мм опреде­ляется путем умножения нормативной для данного района тол­щины Ь„ на поправочный коэффициент к_г, учитывающий влияние местных условий расположения подвески на отложение гололеда:

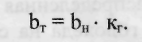(7)

Нормативную толщину стенок гололеда Ь„ в мм на высоте Юме повторяемостью 1 раз в 10 лет в зависимости от заданного гололедного района модно найти по табл. 10.

Таблица 10

Нормативные значение скорости ветра при гололеде и нормативная толщина гололеда

 

Районы территории России по толщине стенки гололеда		II	III	IV	V
Нормативная толщина стенки гололеда Ь„, мм
Нормативная скорость ветра при гололеде vrH, м/с

Значение коэффициента к_г в контрольной работе № 1 в соот­ветствии с заданием (см. примечания к табл. 3) следует принять равным 1.

Вертикальная нагрузка от веса гололеда на контактном про­воде в даН/м определяется по формуле:

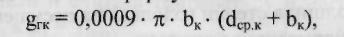(8) где Ь_к - толщина стенки гололеда на контактном проводе, мм;

d_cp к - средний диаметр контактного провода, мм. На контактных проводах толщину стенки гололеда прини­мают равной 50% от толщины стенки гололеда на несущем тросе:

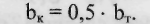(9) Средний диаметр контактного провода в мм:

(10)

где Н и А - соответственно высота и ширина сечения кон­тактного провода, мм принимаются из табл. 5.

 

Остальные величины, входящие в формулу (8), те же, что и в формуле (6).

Полная вертикальная нагрузка от веса гололеда на проводах контактной подвески в даН/м равна:

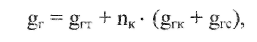(И)

где п_к - число контактных проводов;

g_rc - равномерно распределенная по длине пролета вер­тикальная нагрузка от веса гололеда на струнах и зажимах при одном контактном проводе, даН/м, которая в зависимости от тол­щины стенки гололеда Ь_н составляет:

 

Ь„, мм
grc, даН/м	0,01	0,03	0,06	0,1

Горизонтальная ветровая нагрузка на несущий трос, покры­тый гололедом в даН/м при скорости ветра v_rH, определяется по формуле:

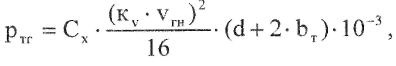(12)

где С_х - аэродинамический коэффициент лобового сопро­тивления несущего троса ветру; табл. 9;

k_v - ветровой коэффициент; в данном расчете принять Ку = 1;

d - диаметр несущего троса, мм;

Ь_т - толщина стенки гололеда на несущем тросе, мм;

v_rH - нормативная скорость ветра при гололеде, м/с; оп­ределяется по табл. 10.

Результирующая (суммарная) нагрузка на несущий трос в режиме гололеда с ветром, даН/'м определяется по формуле:

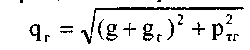(И)

В заключении следует сравнить полученные значения ре­зультирующих нагрузок, действующих на несущий трос в трех расчетных режимах: g; ц„ _тах и q_r и выявить режим наибольшей нагрузки. Для реальных условий на железных дорогах России ре­жимом наибольшей нагрузки чаще всего является режим гололеда с ветром.

 

 

 

 

3. Определение длины эквивалентного и критического про­летов и установление расчетного режима

Длина эквивалентного пролета в м определяется по формуле:

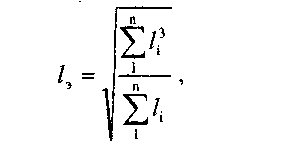
где h - длина пролета с номером ц

п - число пролетов в анкерном участке.

Для дальнейших расчетов полученную длину эквивалентно­го пролета округлить до целого числа.

Из теории механического расчета цепной подвески [1] из­вестно, что для определения по уравнению состояния несущего троса цепной подвески значения натяжения Т_х при любой темпе­ратуре t_x и любой нагрузке q_x, нужно знать исходное состояние (исходный режим), т.е. знать температуру t_b нагрузку qi и соот­ветствующее этим условиям значение натяжения несущего троса

Поскольку первоначально из всех возможных натяжений не­сущего троса известно только его максимальное натяжение Т_тах, то необходимо установить, при каком из расчетных режимов для заданного типа подвески и заданных климатических условий в несущем тросе создается наибольшее натяжение, принять этот режим за исходный и считать температуру и нагрузку при этом режиме за ti и q_b а Т\ = Т_тах.

Таким исходным режимом может быть либо режим мини­мальной температуры (t_min), при которой натяжение в несущем тросе может оказаться наибольшим за счет сжатия материала тро­са, либо режим наибольшей дополнительной нагрузки - режим гололеда с ветром (или режим максимального ветра), при которых натяжение в несущем тросе может оказаться наибольшим за счет растяжения, вызываемого дополнительной нагрузкой на трос от гололеда и ветра.

Чтобы определить, какой из названных режимов для кон­кретных заданных климатических условий и заданного анкерного участка контактной подвески должен быть принят за исходный,

 

 

нужно рассчитать длину критического пролета в м для режима наибольшей дополнительной нагрузки.

Так для режима гололеда с ветром критический пролет равен:

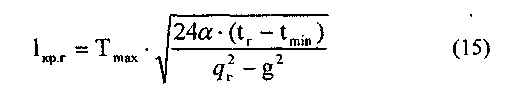
В формуле (15) значение 24а должно быть взято для несу­щего троса заданной подвески по табл. 5.

В соответствии с определением понятия "критический про­лет" - см. [1] - можно сделать вывод, что для того, чтобы натяже­ние в несущем тросе при режиме гололеда с ветром создалось та­кое же, как и при заданной минимальной температуре и было бы равно Т_тах, длина эквивалентного пролета /_э заданного анкерного участка должна быть равна длине /_крг, полученной по формуле (15).

Остается сравнить полученную длину /_{кр г} с найденной выше длиной эквивалентного пролета /_э для заданного анкерного участ­ка цепной подвески.

Если окажется, что значение критического пролета больше 1_э (4_Р.г > h), то исходный расчетный режим - минимальная темпера­тура.

Если окажется, что значение /кр_Г меньше, чем /_э (/кр._г < 4)> то исходный расчетный режим - режим гололеда с ветром.

4. Определение натяжений несущего троса. Построение монтажной кривой Ту (О. Составление монтажной таблицы

4.1. Расчет зависимости натяжения нагруженного несущего троса от температуры и построение монтажной кривой Т_х (t _v).

Расчет зависимости Т_х (t_x) выполняется по уравнению со­стояния несущего троса цепной полукомпенсированной контакт­ной подвески

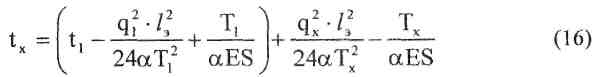
В уравнении состояния величины с индексом " 1" относятся к исходному режиму, при котором Т, = Т_тах (наибольшее допускае­мое натяжение):

 

 

а) если исходный расчетный режим -минимальная темпера­
тура, то Tj = T_rnax; tj = t_rain; qj = g;

б) если исходный расчетный режим - гололед с ветром, то
Ti = T_max; t] = t_r = -5 С; qi = q_r.

Величины с индексом "х" в уравнении состояния - это ис­комые значения натяжения несущего троса Т_х и соответствующие им значения температуры t_x и нагрузки q_x.

При этом, поскольку вначале предстоит рассчитать зависи­мость натяжения несущего троса только от температуры Т_х (t_x), без учета влияния дополнительных нагрузок от ветра и гололеда, то в данном разделе расчета следует принять q_x = g.

Значения произведений 24а и aES для несущего троса за­данной подвески должны быть взяты из табл. 5.

Для упрощения дальнейшего расчета уравнение состояния может быть приведено к виду:

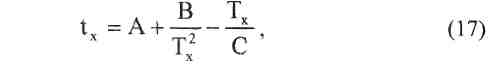
где А, В, С - постоянные для данного расчета коэффициен­ты:

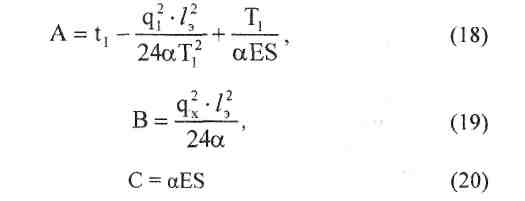
Подставляя в уравнение (17) различные значения Т_х, взятые с интервалом 200 даН, получают соответствующие им значения t_x. Начать следует с Т_х - Т_тах. Расчет следует продолжать до тех пор, пока значениями t_x не будет охвачен весь заданный диапазон температур от t_min до t_max - в итоге будет получен ряд значений (Т_х, t_x), которые удобно свести в промежуточную таблицу и по этим результатам построить на листе миллиметровой бумаги кри­вую Т_х (t_x) - монтажную кривую натяжения нагруженного (кон­тактным проводом) несущего троса полукомпенсированной цеп­ной подвески в зависимости от температуры.

 

 

При построении кривой Т_х (t_x) рекомендуется принять мас­штаб:

по вертикали (Т_х) 10 мм - 100 даН;

по горизонтали (t_x) 10 мм - 10°С,

ось Т_х следует провести через 0°С.

4.2. Определение натяжений несущего троса при всех трех расчетных режимах:

при минимальной температуре T_tm;_n;

при максимальном ветре T_{v max};

при гололеде с ветром Т_г.

Один из этих расчетных режимов, как это определено выше, является исходным расчетным, натяжение несущего троса при этом режиме равно максимальному Т_тах (см. определение исход­ного расчетного режима).

Таким образом, предстоит определять значения натяжения несущего троса при двух режимах (кроме исходного).

При этом обычно возможны два варианта расчета в зависи­мости от установленного выше исходного расчетного режима для уравнения состояния несущего троса полукомпенсированной кон­тактной подвески:

а) Если исходным расчетным режимом оказался режим ми­нимальной температуры, то значение T_{t min} = T_max.

Находить же нужно в этом случае натяжение несущего троса при максимальном ветре T_v max и при гололеде с ветром Т_г.

Значения T_{v max} и Т_г определяются методом подбора по урав­нению состояния несущего троса полукомпенсированной кон­тактной подвески (17).

Для этого в уравнении состояния величины с индексом "1" следует отнести к исходному расчетному режиму, т.е. так же, как и в предыдущем расчете, в данном случае будет

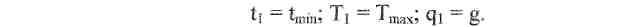
Иными словами, коэффициент А в уравнении состояния (в его упрощенном виде) будет иметь найденное в предыдущем рас­чете значение; коэффициент С также остается прежним. Уравне­ние состояния приобретает вид:

 

 

 

 

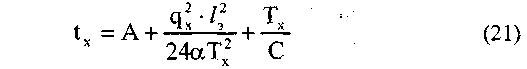
Величины с индексом "х" в уравнении состояния следует вначале отнести к режиму максимального ветра, а затем - к ре­жиму гололеда с ветром.

Метод подбора состоит в следующем:

Пусть вначале определяется значение T_{v max}. Тогда в уравне­нии состояния q_x = q_{v max}.

Значение q_vmax найдено ранее по формуле (5).

Далее следует произвольно задаться значением T_v max и при­нять его за Т_х.

Примечани е. Для ускорения расчета следует начать подбор со значения Т_х, несколько большего, чем значение Т_х на кривой, соответствующее температуре t_x = t _{v max} = -5 С. Можно также ори­ентироваться на данные табл. 6.

Пусть, например, задались Т_х = 1400 даН. Подставив значе­ния q_x и Т_х в уравнение состояния (21), вычислим t_x. Пусть полу­чилось t_x = -3,5° (а рассчитывали получить (-5°)).

Возьмем большее значение Т_х = 1500 даН, подставим в уравнение (21); пусть при этом получилось t_x = -6,5°.

Температура t_vmax = -5° оказалась между двумя полученными t_x; значение T_{v max} также будет между двумя принятыми выше зна­чениями Т_х.

Действительное значение T_{v raax} найдем методом линейной интерполяции. В нашем примере будет:

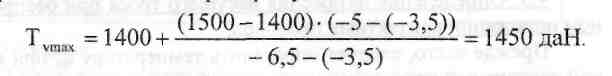
Аналогично методом подбора определяется и значение Т_г. В этом случае в уравнении состояния (21) величины с индексом "х" должны относится к режиму гололеда с ветром, т.е. q_x = q_r.

Значение q_r найдено выше по формуле (13).

Значениями Т_х = Т_г задаются и ожидают получить при под­становке q_x и Т_х в уравнение состояния (21) значение:

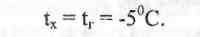
Полученные значения T_v max и Т_г должны быть точками с ко­ординатами (T_v щи, t_vmax) и (T_r, t_r) отмечены над кривой Т_х (t_x).

б) Если исходным расчетным режимом оказался режим го­лоледа с ветром, то значение Т_г = Т _тах.

 

 

 

Находить же нужно в этом случае натяжение несущего троса при максимальном ветре T_{v max} и при минимальной температуре

11 min-IS этом случае в уравнении состояния величины с индексом "1", относящиеся к исходному расчетному режиму, имеют сле­дующие значения:

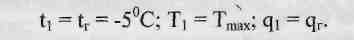
Коэффициенты А и С в уравнении состояния (в его упро­щенном виде) будут иметь значения, найденные ранее при расче­те кривой Т_х (t_x).

Натяжение несущего троса при режиме максимального ветра T_{v max} можно определить по уравнению состояния (21) методом подбора; так как это описано выше, принимая:

Значение натяжения несущего при режиме минимальной температуры также можно определить методом подбора по урав­нению состояния несущего троса, приняв:

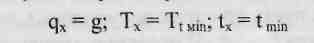
Однако, это можно сделать проще: значение несущего троса при режиме минимальной температуры может быть определено по монтажной кривой Т_х (t_x), построенной выше, соответственно температуре t_mi_n.

4.3. Определение натяжения несущего троса при беспровес­ном положении контактных проводов.

Прежде всего, следует определить температуру to, при кото­рой контактный провод будет занимать беспровесное положение.

Для полукомпенсированной цепной подвески температуру to беспровесного положения контактных проводов обычно прини­мают несколько ниже (на величину f), чем среднее значение тем­пературы в заданном районе. В связи с этим, формула для опреде­ления температуры беспровесного положения контактных прово­дов может быть записана так:

 

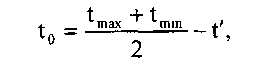
где t' - величина, зависящая от типа и количества контакт­ных проводов; ее значения приведены в табл. 11.

 

Таблица 11

 

Для одиночных контактных проводов сечением 85-100 мм2	f = 15°
Для одиночных контактных проводов сечением 150 мм2	t'=10°-M5°
Для двойных контактных проводов	f = 5°+10°

Величину натяжения несущего троса при беспровесном по­ложении контактных проводов Т₀ следует определить по постро­енной выше монтажной кривой натяжения несущего троса Т_х (t_x) соответственно найденной температуре беспровесного положения контактных проводов to.

4.4. Составление монтажной таблицы натяжения несущего троса.

По монтажной кривой натяжения нагруженного несущего троса Т_х (t_x) определяют значения натяжения несущего троса, со­ответствующее заданным значениям t_x и заносят их в монтажную таблицу по образцу табл. 12.

Таблица 12 Монтажная таблица натяжений несущего троса

 

lx> v^	Tmin=…	-20	t0=...		+20	tmax
; Тх,даН			Т0 =...

Примечания:

1. Графа температуры беспровесного положения контакт­ных проводов t₀ в каждом варианте должна быть распо­ложена в порядке повышения температуры слева напра­во.

2. Под монтажной таблицей следует указать найденные выше значения натяжений T_{v ma}x, T_r.

5. Расчет и построение монтажных кривых стрел провеса не­сущего троса и контактных проводов

5.1.Определение стрел провеса нагруженного несущего троса.

Стрелы провеса нагруженного контактного проводом несу­щего троса F_x в м для каждого из заданных действительных про­летов, входящих в анкерный участок, определяют по формуле:

 

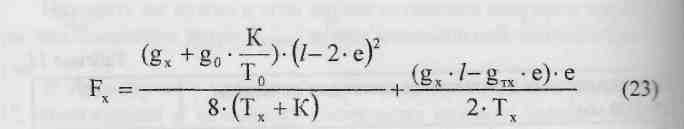
В этой формуле:

/ - длина пролета в м, для которого рассчитывается стрела провеса несущего троса;

е - расстояние от опоры до первой простой (нерессорнойО струны в м; задано в табл. 1;

К - натяжение контактных проводов в даН;

Т₀ - натяжение несущего троса при беспровесном положе­нии контактных проводов в даН, определено выше;

Т_х - натяжение несущего троса в даН, соответствующее температуре t_x, для которого рассчитывается значение стрелы провеса F_x;

go - вертикальная нагрузка на несущий трос от веса всех проводов цепной подвески при беспровесном положении кон­тактных проводов в даН/м, т.е. go = g;

g_x - вертикальная нагрузка на несущий трос от веса всех проводов цепной подвески, соответствующая расчетным услови­ям, даН;

g_TX - нагрузка от веса несущего троса при расчетных услови­ях, даН.

Поскольку в данном расчете определяются значения F_x в за­висимости только от температуры, без учета гололеда и макси­мального ветра, то g_x = g₀ = g - подсчитана по формуле (3), g„ = g_T (взять из табл. 3).

Из формулы (23) следует, что расчет стрел провеса несущего троса должен быть выполнен отдельно для каждой заданной дли­ны пролета и отдельно для каждой заданной температуры t_x, т.е. для соответствующих заданным температурам значений натяже­ний несущего троса Т_х. Такой расчет рационально сделать в таб­лице по образцу табл. 13.

 

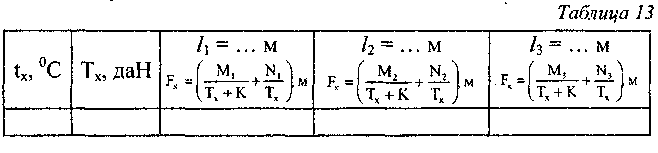
Значения Т_х, соответствующие заданным температурам, t_x, принимаются по составленной выше монтажной таблице натяже­ний несущего троса (табл. 12). Все прочие величины, кроме Т_х, входящие в формулу (23), не зависят от изменения температуры, что позволяет упростить формулу (23), предварительно определив Mi, М₂, Мз и Ni, N2, N3 - числовые значения не зависящих от тем­пературы t_x частей формулы (23) соответственно для длин проле­тов /_ь /₂, /₃:

Для .

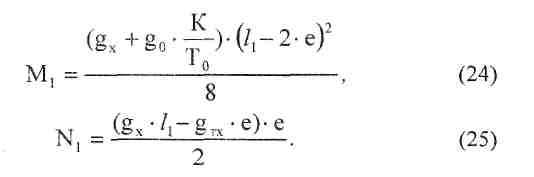
Аналогично для /₂, /₃ определяются М₂, N₂ и М₃, N₃

На основании итогов расчета стрел провеса несущего троса нужно построить монтажные кривые стрел провеса несущего тро­са F_x (t_x).

При построении кривых F_x (t_x) рекомендуется принять мас­штаб:

по вертикали (F_x) 10 мм - 0,1 м;

по горизонтали (t_x) 10 мм - 10°С;

ось F_x следует провести через 0°С.

5.2. Определение стрел провеса контактных проводов.

Стрелы провеса контактных проводов f_KX в м определяются

по формуле:

 

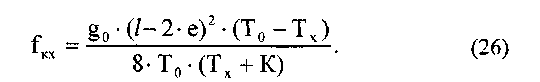
Все величины, входящие в формулу f_KX (26) объяснены при­менительно к формуле (23).

Из формулы (26) видно, что стрелы провеса контактных проводов должны быть определены в том же порядке, что и стре­лы провеса несущего троса, т.е. отдельно для каждой заданной длины пролета и отдельно для каждой заданной температуры t_x (для каждого значения Т_х, соответствующего заданным значениям температуры t_x).

 

 

 

 

Расчет fja рационально выполнить в таблице, аналогичной табл. 13, предварительно определив для каждой длины пролета не зависящую от температуры часть формулы (26) обозначив ее Д. Например для ;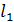

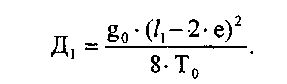
Аналогично определяют Д₂ и Д₃ для l₂ и l₃.

По окончании расчетов стрел провеса контактных проводов следует себя проконтролировать, убедившись,

что при t_x ниже to f_KX - отрицательны и тем больше, чем ниже температура;

4TonpHt_x = to f_Kx = 0;

что при t_x выше to - f^ положительны и тем больше, чем выше температура.

Если эта зависимость нарушена, значит в расчете f^ есть ошибки.

На основании итогов расчета стрел провеса f_KX следует по­строить монтажные кривые стрел провеса контактных проводов

fKx(t_x).

При построении кривых f_KX (t_x) рекомендуется принять мас­штаб:

по вертикали (f_KX) 10 мм - 0,01 м; по горизонтали (t_x) 10 мм - 10°С; ось ^ следует провести через 0 С.

6. Составление итоговой монтажной таблицы, Выводы из расчета

Полученные для заданных значений t_x величины натяжения Т_х и стрел провеса F_x несущего троса, а также стрел провеса кон­тактных проводов f^ следует свести в итоговую монтажную таб­лицу по образцу табл. 14.

 

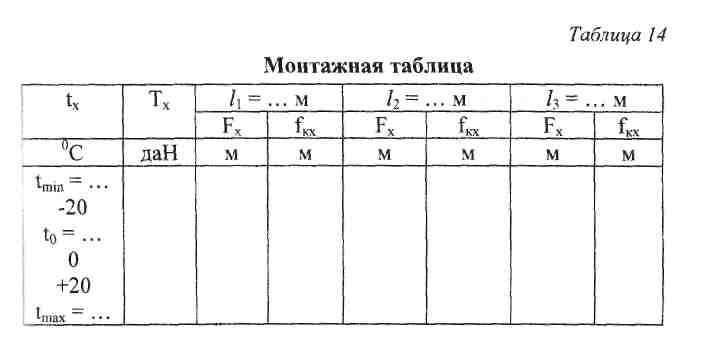
В выводах, как это указано в задании, необходимо пояснить, как изменяются натяжение несущего троса Т_х и стрелы провеса несущего троса F_x и контактных проводов f^ полукомпенсиро­ванной контактной подвески при изменении температуры от t_min

ДО 1щах*

Выводы должны быть сделаны на основании анализа поме­щенной выше итоговой монтажной таблицы, в которой изменение всех перечисленных параметров контактной подвески при изме­нении температуры окружающего воздуха представлено нагляд­но.

При формировании выводов необходимо особое внимание уделить олисанию изменения стрел провеса контактных проводов при изменении температуры, указав, как изменяется стрела про­веса контактных проводов f_KX при изменении температуры:

от t_min до t₀;

ОТ to ДО tmaxJ

какой будет f_KX при t_x = to.

Кроме этого следует указать, как влияет длина пролета на величины Fj и f_KX.