Определение коэффициента режима работы

Ресурс передачи определяется по зависимости

t = L 365 К_год 24 К_сут – (10…25%), (час)

где L – число лет работы передачи;

К_год – коэффициент использования передачи в течение года;

К_сут – коэффициент использования передачи в течение суток;

10…25% – время необходимое на профилактику, текущий ремонт, нерабочие дни.

t = 5 ´ 0,6 ´ 365 ´ 24 ´ 0,3 – 10% = 7096 час.

Расчёт зубчатых передач

Расчёт зубчатых закрытых передач производится в два этапа. На первом этапе выполняется проектный расчёт, согласно которому по допускаемых контактным напряжениям определяются геометрические параметры взаимодействующих зубчатых колёс. В процессе этого выбираются табличные значения, некоторые из вычисленных величин округляются до стандартных значений. Проверочный расчёт, выполняемый на втором этапе, окончательно подтверждает правильность или указывает на неверно выбранные значения, а также определяет соотношения между расчётными и допускаемыми изгибными напряжениями.

2.4.1 Выбор твёрдости, термообработки
и материала зубчатых колёс

Эквивалентное число циклов нагружения зубьев при расчете на контактную прочность

,

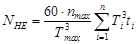где Т_max – максимальный крутящий момент (по графику нагрузки);

t_max – время действия максимального момента;

n_max – число оборотов при максимальном моменте.

В нашем случае (n₁ = n = const, Т_max = Т_н) эквивалентное число циклов нагружения зубьев шестерни при расчете на контактную прочность

,

или

N_HE1 = 60 ´ n_вх ´ t ´ (0,2 + 0,7³ ´ 0,3 + 0,4³ ´0,5),

где n₁ – число оборотов шестерни, мин^-1;

Т_н – номинальный крутящий момент шестерни, Нм;

t – время работы зубчатой передачи (ресурс), час.

N_HE1 = 60 ´ n_вх ´ t ´ (0,2 + 0,7³ ´ 0,3 + 0,4³ ´0,5)

N_HE1 = 60 ´ 1224 ´ 7096 ´ (0,2 + 0,7³ ´ 0,3 + 0,4³ ´0,5) =
= 1,75´10⁸

Эквивалентное число циклов нагружения для зубьев колеса

Эквивалентное число циклов нагружения при расчёте на изгиб

.

Для шестерни

N_FE1 = 60 ´ n_вх ´ t ´ (0,2 + 0,7⁹ ´ 0,3 + 0,4⁹ ´0,5)

N_FE1 = 60 ´ 1224 ´ 7096 ´ (0,2 + 0,7⁹´0,3 + 0,4⁹´0,5) = 1,1 ´ 10⁸

Эквивалентное число циклов нагружения для зубьев колеса

.

Материал зубчатой пары выбираем по таблице 7. Допускаемые контактные напряжения в зависимости от принятого материала определяют по таблице 8, термическая обработка и механические характеристики металла по таблице 9.

Принимаем материал шестерни и колеса – сталь 40X. Термообработка – улучшение. Твёрдость шестерни – 280НВ, колеса – 260НВ. s_в = 790 МПа.

Коэффициент долговечности при расчёте на контактную прочность

,

Базовое число циклов, соответствующее пределу выносливости для шестерни и зубчатого колеса равно N_{H lim} = 10⁷.

Поскольку N_НE1 > 10⁷ и N_HE2 > 10⁷, то К_H = 1,0.

Определение коэффициента долговечности при расчете на изгиб

,

Таблица 7 – Материалы зубчатых колёс

Шестерня	Зубчатое колесо
40Л
45Л
Ст5
45Л
Ст5
40Х
40Х
40ХЛ
45Х	40Х
45ХН	40Х
45Х

Таблица 8 Допускаемые контактные и изгибные напряжения
для зубчатых колес [1]

Группа сталей	Контактное sHlim, МПа	SHmi n	Изгибное sFlim, МПа	SF	[ sH ] max, МПа	[ sF ] max, МПа
40, 45, 40Х, 40ХН, 45ХЦ, 35ХМ	2HB + 70	1,1	1,8 HB	1,75	2,8sт	2,74 HB
40Х, 40ХН, 45ХЦ, 36ХМ	18HRC + 150		2,8sт
55ПП, У6, 35ХМ	17НRCпов +200	1,2		40HRCпов
40Х, 40ХН 35ХМ, 40Х, 40ХН	17НRCпов + 200		40HRCпов	>>
35ХЮА, 38ХМЮА, 40Х 40ХФА, 40ХНМА	>>		12HRCсердц + 300
	1,75	40HRCпов 30HRCпов	>>
Цементируемые стали всех марок	23HRCпов		1,5	40HRCпов
Молибденовые стали 25ХГМ, 25ХГНМ	23HRCпов		40HRCпов
Безмолибденовые стали 25ХГТ, 30ХГТ, 35Х	23HRCпов		40HRCпов

Таблица 9 Термическая обработка сталей для зубчатых колес [1]

Марка стали	sB, МПа	sТ, МПа	Термическая обработка
			Нормализация
			Нормализация
			Улучшение
			Улучшение
40Х			Улучшение
40Х			Улучшение
40Х			Улучшение + закалка ТВЧ
35ХМ			Улучшение
35ХМ			Улучшение
35ХМ			Улучшение + закалка ТВЧ
40ХН			Улучшение
40ХН			Улучшение
40ХН			Улучшение + закалка ТВЧ
20ХНМ			Улучшение + цементация + закалка
18ХГТ			Улучшение + цементация + закалка
12ХНЗА			Улучшение + цементация + закалка
25ХГМ			Улучшение + цементация + закалка
40ХНМА			Улучшение + азотирование
35Л			Нормализация
45Л			Улучшение

 

Базовое число циклов напряжений N_{F lim} = 4 ´10⁶.

Если N_FE ≥ 4·10⁶, то следует принять К_F = 1,0.

Для углеродистых и легированных сталей любых марок при HB ≤ 350 (нормализация и улучшение) допускаемые контактные напряжения определяют по зависимости

[σ]_H = σ_{H lim} K_H Z_R Z_V /S_H,

где σ_{H lim} – предел контактной выносливости при базовом числе циклов нагружения;

K_H – коэффициент долговечности;

Z_R – коэффициент, учитывающий шероховатость поверхности зубьев (для приближенных расчетов Z_R = 1,0);

Z_V – коэффициент, учитывающий окружную скорость (для приближенных расчетов можно принимать Z_V = 1,0);

S_H – коэффициент запаса прочности. Для зубчатых колёс при нормализации и объемной закалке S_H =1,1. Для зубчатых колёс с поверхностным упрочнением зубьев S_H = 1,2.

Поскольку допускаемое контактное напряжение для колеса меньше, чем для шестерни, примем его в качестве расчетного. Тогда

[ σ ] _H = (2´ 260 + 70)´1´1´1 /1,1 = 536 МПа.

Допускаемые изгибные напряжения выбирают для двух случаев нагружения.

Одностороннее действие нагрузки (отнулевой цикл)

,

где [n] – требуемый коэффициент запаса прочности, [n]=1,4…2,2;

К_F – коэффициент долговечности при изгибе;

К_σ – эффективный коэффициент концентрации напряжений у ножки зуба, К_σ = 1,4…1,6;

σ_-1 – предел выносливости сталей:

для углеродистых сталей σ_-1 ≈ 0,43 σ_В МПа;

для легированных сталей σ_-1≈0,35 σ_В +(70…120) МПа.

Переменное направление нагрузки (симметричный знакопеременный цикл)

В нашем случае зубчатая передача испытывает одностороннее действие нагрузки, поэтому допускаемое напряжение изгиба

МПа.

2.4.2 Прочностной расчёт
цилиндрических закрытых передач

Вычислим предварительное значение межосевого расстояния

,

где K – коэффициент зависящий от поверхностной твёрдости зубьев, для твёрдости шестерни и колеса H₁ £ 350 HB и
H₂ £ 350 HB K = 10;

U_ред – передаточное число одноступенчатого цилиндрического редуктора;

+ (–) – знак, учитывающий внешнее (внутреннее) зацепление;

Т_вх – номинальный крутящий момент на шестерне в Нм.

мм.

По найденному предварительному значению межосевого расстояния определим окружную скорость в зацеплении

, м/с,

где n_вх – частота вращения входного вала редуктора.

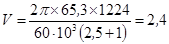м/с.

По таблице 10 исследуемая зубчатая передача 8 степени точности.

Таблица 10 Рекомендуемая степень точности изготовления
зубчатых передач

Степень точности по ГОСТ 1643–81	Окружная скорость V, м/с
прямозубые	непрямозубые
6 (передачи повышенной точности)	до 20	до 30
7 (передачи нормальной точности)	до 12	до 20
8 (передачи пониженная точности)	до 6	до 10
9 (передачи низкой точности)	до 2	до 4

 

Уточняем предварительно найденное значение межосевого расстояния цилиндрической зубчатой передачи

,

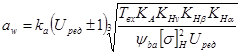где k_a = 450 – вспомогательный коэффициент для прямозубых колёс;

K_А – коэффициент внешней динамической нагрузки, K_А = 1,0 (таблица 11);

K_Hv – коэффициент внутренней динамики нагружения; интерполируя значения по таблице 12 получим K_Hv = 1,12;

K_Hb – коэффициент неравномерности распределения нагрузки по ширине венца (рисунок 2);

K_Ha – коэффициент распределения нагрузки между зубьями; по ГОСТ 21354–87 для прямозубых передач K_Ha = 1,0;

y_ba = 0,4 – коэффициент ширины шестерни относительно межосевого расстояния, выбирается из ряда стандартных чисел: 0,1; 0,15; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63 в зависимости от положения зубчатого колеса относительно опор (при симметричном расположении – y_ba = 0,315…0,5);

[σ]_H – допускаемое контактное напряжение в МПа.

Для определения коэффициента K_Hb необходимо вычислить коэффициент ширины шестерни относительно её диаметра y_bd

.

.

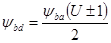Величина коэффициента K_Hb = 1,06 (рисунок 2).

мм,

Определение ширины венцов:

зубчатого колеса

,

b₂ = 0,4 ´ 63,95 = 26 мм.

шестерни

b₁ = b₂ + (3…5)

b₁ = 26 + 4 =30 мм.

Примем предварительно число зубьев шестерни и определим модуль зацепления

, мм

Таблица 11 Значения коэффициента
внешней динамической нагрузки K_А

Режим нагружения двигателя	Режим нагружения ведомой машины
	Равномерный	1,00	1,25	1,50	1,75
	С малой неравномерностью	1,10	1,35	1,60	1,85
	Со средней неравномерностью	1,25	1,50	1,75	2,00 и выше
	Со значительной неравномерностью	1,50	1,75	2,00	2,25 и выше

Пояснение к таблице 11.

Характерные режимы нагружения двигателей:

равномерный – электродвигатели;

с малой неравномерностью – гидравлические двигатели;

со средней неравномерностью – многоцилиндровые двигатели внутреннего сгорания;

со значительной неравномерностью – одноцилиндровые двигатели внутреннего сгорания.

Характерные режимы нагружения ведомых машин:

равномерный – равномерно работающие ленточные, пластин­чатые конвейеры, легкие подъемники, вентиляторы и т.д.;

с малой неравномерностью – неравномерно работающие лен­точные и пластинчатые транспортеры, шестеренчатые и рота­ционные насосы, главные приводы станков, тяжелые подъемники, крановые механизмы, промышленные и рудничные вен­тиляторы, поршневые многоцилиндровые насосы, станы хо­лодной прокатки и т.д.;

со средней неравномерностью – мешалки для резины и пластмасс, легкие шаровые мельницы, деревообрабатывающие стан­ки, одноцилиндровые поршневые насосы и т.д.;

со значительной неравномерностью – экскаваторы, черпалки, тяжелые шаровые мельницы, дробилки, буровые машины, станы горячей прокатки и т.д.

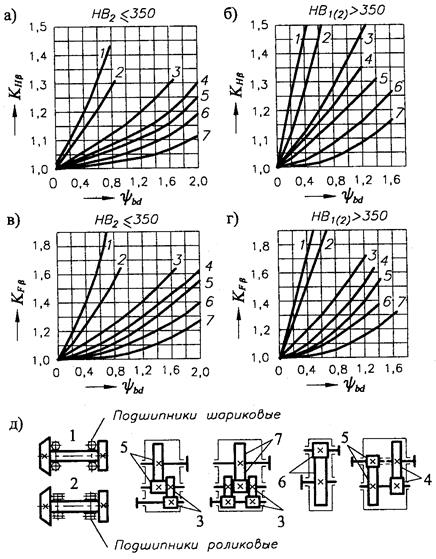
Рисунок 2 – Графики для определения коэффициентов неравномерности распределения нагрузки по ширине венца:
а) и б) при расчете контактной прочности зубьев K_Hβ, в) и г) при расчете зубьев на изгиб K_Fβ для схем редукторов 1-7; д) схемы редукторов

Таблица 12 – Значения коэффициента внутренней динамики нагружения K_Hv для прямозубых зубчатых колес

Степень точности по ГОСТ 1643-81	Твердость на поверхности зубьев колеса	Значения KHv при v, м/с
	> 350 НВ	1,02	1,06	1,10	1,16	1,20
£ 350 НВ	1,03	1,09	1,16	1,25	1.32
	> 350 НВ	1,02	1,06	1,12	1,19	1,25
£ 350 НВ	1,04	1,12	1,20	1,32	1,40
	> 350 НВ	1,03	1,09	1,15	1,24	1,30
£ 350 НВ	1,05	1,15	1,24	1,38	1,48
	> 350 НВ	1,03	1,09	1,17	1,28	1,35
£ 350 НВ	1,06	1,12	1,28	1,45	1,56

 

мм.

Полученное расчётное значение m¢ округлим до ближайшей величины m = 2,0 мм, в соответствии с ГОСТ 9563–80 (таблица 13).

Таблица 13 – Модули зубчатых колес по ГОСТ 9563-80 (мм)

1-ряд		1,25	1,5		2,5
2-ряд	1,125	1,375	1,75	2,25	2,75	3,5	4,5	5,5

 

Определяем действительное число зубьев шестерни, при этом должны выполняться следующие условия z₁ – целое число и z₁ ³ 17

,

.

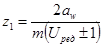Окончательно выбираем число зубьев шестерни z₁ = 18.

Определяем число зубьев колеса

z₂ = z₁ ´ U.

z₂ = 18 ´ 2,5 = 45.

Окончательно выбираем число зубьев колеса z₂ = 45.

Действительное передаточное число зубчатой передачи

.

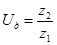
Диаметры начальных окружностей (определяются с точностью до 2 знака после запятой)

d_w =m´ z.

для шестерни

d_w1 = 2,0 ´ 18 = 36 мм

для колеса

d_w2 = 2,0 ´ 45 = 90 мм

Диаметры вершин зубьев (определяются с точностью до 2 знака после запятой)

d_а =m´ (z + 2);

для шестерни

d_а1 = 2,0 ´ (18 + 2) = 40 мм;

для колеса

d_а2 = 2,0 ´ (45 + 2) = 94 мм.

Расчётное межосевое расстояние

мм

Вычисленное значение межосевого расстояния а_w округляют до ближайшего стандартного значения по ГОСТ 2185-88 по ряду размеров Ra 40 (таблица 14). Ближайшее стандартное значение а_w = 63 мм.

Таблица 14 – Межосевые расстояния по ГОСТ 2185–88, мм

1 ряд
2 ряд