Пример выполнения задания.

Определить реакции шарнирно-подвижной и шарнирно-неподвижной опор балки, нагруженной силой F и парой с моментом М. Весом балки пренебречь.

F = 8 кН; М =14 кН·м; l₁ = AC = 0,8м; l₂ = CD = 0,6м; l₃ = DB = 0, 4 м.

 

 

 

 

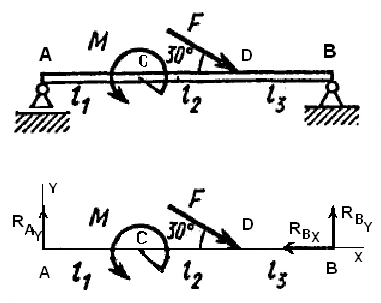
Балка находится в равновесии. Отбрасываем связи (опоры) А и В. Заменяем их действие реакциями. Реакция шарнирно- подвижной опоры А направлена по нормали вверх – R_AY. Горизонтальная составляющая отсутствует. R_BXи R_BY - составляющие реакции шарнирно-неподвижной опоры В.

Составляем три уравнения равновесия.

1. ∑ М_А = 0 М – F · Cos 60⁰ ·AD + R_BY· AB = 0

14 – 8 · 0, 5 · 1,4 + R _BY · 1,8 = 0

R _BY = - 4,67кН

2. ∑ М_В = 0 - R _AY · AB + M – F · Cos 60⁰ · BD = 0

-R _AY · 1,8 + 14 + 8 · 0,5 · 0,4 = 0

R _AY = 8,67кН

 

3. ∑ F _X = 0 F · Cos 30⁰ - R _BX = 0

8 · 0,866 - R_{BX = 0}

R_BX = 6,93 кН

 

Проверка

∑ F _Y = 0 R _AY - F · Cos 60⁰ + R _BY = 0

8,67 - 8 · 0,5 + (- 4,67) = 0

0 = 0

Расчет верен. Реакция R_BYдолжна быть направлена вниз.

 

Контрольные вопросы.

 

1. Какие системы сил называются эквивалентными?

2. В чем сходство между равнодействующей и уравновешивающей силами и чем они отличаются друг от друга?

3. Если две непараллельные силы, лежащие в одной плоскости

приложены в разных точках твердого тела, можно ли при их

сложении применить правило параллелограмма (или треугольника)

и в какой точке будет приложена равнодействующая этих сил?

4. Можно ли силу в 50 Н разложить на две силы, например, по

200 Н?

5. Какие разновидности связей рассматриваются в статике?

 

 

Литература.

 

Аркуша А.И. Техническая механика: Теоретическая механика и сопротивление материалов: Учебник для машиностроительных специализированных техникумов.- 2-е изд., доп.-М.: Высшая школа, 2008.- 352 с., ил.

 

 

Практическое занятие №3.

Определение центра тяжести сечения, составленного из стандартных прокатных профилей.

Цель работы.

Научится анализировать конфигурацию сложных плоских сечений тел, их рациональное разбиение на простые и симметричные фигуры, успешно решать задачи по определению центра тяжести однородных тел.

Задание.

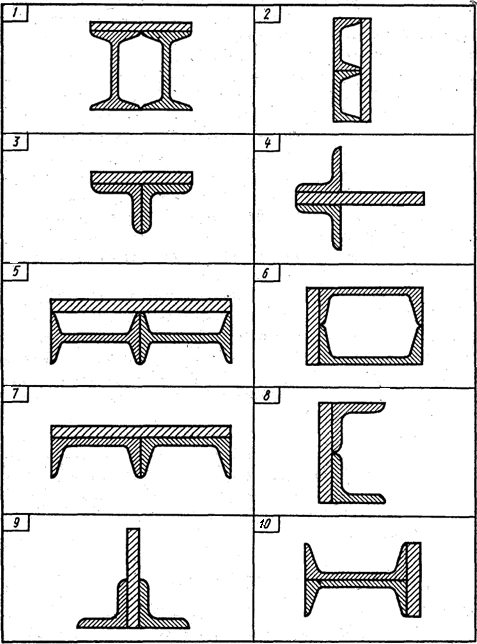
В соответствии с исходными данными для соответствующей схемы (из таблицы для своего варианта) сечения, составленного из приваренных друг к другу прокатных профилей определить координаты центра тяжести этого сложного сечения.

 

№ вар	№ схемы	№ профиля	сечение полосы, мм	№ вар	№ схемы	№ профиля	сечение полосы, мм
			25х320			10.	14х110
			15х100				14х240
			15х 180				10х80
			9х90				14х100
			25х660				20х280
		6,5	25х72				20х140
			15х540				14х160
			15х220				10х280
			15х 150				14х200
			25х210				16х310
			25х270				20х128
			20х240				15х360
			15х160				12х160
			15х180				15х200
			18х400				18х80

 

Схемы плоских сечений

 

С

 

 

 

Общие сведения.

Силы притяжения отдельных частиц тела направлены к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Рав­нодействующая этих параллельных сил, равная их сумме, есть вес тела, а центр этой системы параллельных сил, в котором приложен вес тела, называется центром тяжести тела. Чтобы найти поло­жение центра тяжести тела, необходимо изучить, как складывают­ся параллельные силы и определяются координаты точки приложе­ния их равнодействующей.

В случаях, когда тело можно разбить на конечноечисло простых элементов, применяется способ разбиения на фигуры, положение центров тяжести которых известно. Координаты центра тяжести всего сечения в этом случае определяют по формулам:

X_C= (∑A_IX_I) / A; Y_C= (∑A_IY_I) / A,

где A_I – площадь I-го элемента разбиения, а X_I и Y_I - координаты его центра тяжести; A - суммарная площадь сечения всех элементов.

Геометрические характеристики простых фигур (сечение полосы – прямоугольник) рассчитываются аналитически, характеристики сечений двутавров, швеллеров и уголков принимаются по таблицам сортамента на металлопрокат (соответственно ГОСТ 8239-89; 8240-97 и 8509-93).