Пример выполнения задания.

ОП 00 ОП.03. ТЕХНИЧЕСКАЯ МЕХАНИКА

 

Методическое пособие

По проведению практических занятий

Для специальностИ

Строительство железных дорог, путь и путевое хозяйство

Базовая подготовка среднего профессионального образования

 

 

Ростов-на-Дону

 

 

 

 

РАССМОТРЕНО

Предметной (цикловой)

комиссией

«Специальности

общепрофессиональных

и социально-экономических

дисциплин»

Протокол №_______

От __________2014 г.

 

 

Председатель комиссии

__________А. С. Родионов

Методические пособие по проведению практических

занятий разработаны

на основе рабочей программы,

учебной дисциплины

«Техническая механика», специальности08.02.10«Строительство железных дорог, путь и путевое хозяйство (базовый уровень)»

 

Заместитель директора

по учебной работе

__________И. В. Дурынин

 

 

Автор — канд.техн.наук, доцент Байер А.Б.

 

 

Практическое занятие №1

Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способом.

 

Цель работы.

Получение твёрдых навыков в решении задач на равновесие тел, обратив особое внимание на рациональный выбор направления координатных осей.

Задание.

В соответствии с исходными данными таблицы для своего варианта определить силу натяжения троса, удерживающего в равновесии шар весом G, а также силу давления шара на опорную плоскость.

 

 

№ вар.	G, Н	α, град	β, град	№ вар.	G, Н	α, град	β, град

 

Общие сведения.

Статика, рассматривая равновесие системы действующих на тело сил, дает правила для определения входящих в эту систему неиз­вестных сил. Знание модулей и направлений всех действующих на тело сил необходимо при выполнении большинства технических расчетов курса технической механики.

При рассмотрении равновесия тела, наложенные на него связи следует отбросить, заменив их действие реакциями (т. е. силами действия связей на тело). Реакция гладкой опорной по в е р х н о с т и направлена по нормали к этой поверхности в сторону к телу. Реакция точечной опоры (ребро двугранного угла) направлена по нормали к гладкой поверхности опирающегося тела в сторону к телу. Реакция гибкой связи (трос, нить и т. п.) направлена вдоль связи в сторону от тела. Гибкая связь, перекинутая через блок, изменяет направ­ление передаваемой силы без изменения ее моду­ля. Реакция жесткого прямого стер ж н я с шарнирным закреплением концов направлена вдоль его оси в сторону от тела (если стержень нагружен растягивающей силой) или в сторону к телу (если эта сила сжимающая). Реакция ш а р н и р н о - п о д в и ж н о й опоры нап­равлена по нормали к опорной поверхности,шарнира. Реакцию шар н и рно-неподвижной опоры приня­то представлять в виде двух составляющих реакций по осям координат. В заделке помимо двух составляющих реакций по осям координат возникает реактивный момент.

При аналитическом методе решения применяемая система двух урав­нений равновесия имеет вид ∑F_x = 0; ∑ F_y = 0(сумма проекций сил системы на каждую из координатных осей равна нулю).

Проекция силы на ось равна произ­ведению модуля силы на косинус ее острого угла с осью. Знак проек­ции определяется совпадением направлений проекции и оси.

 

 

Пример выполнения задания.

 

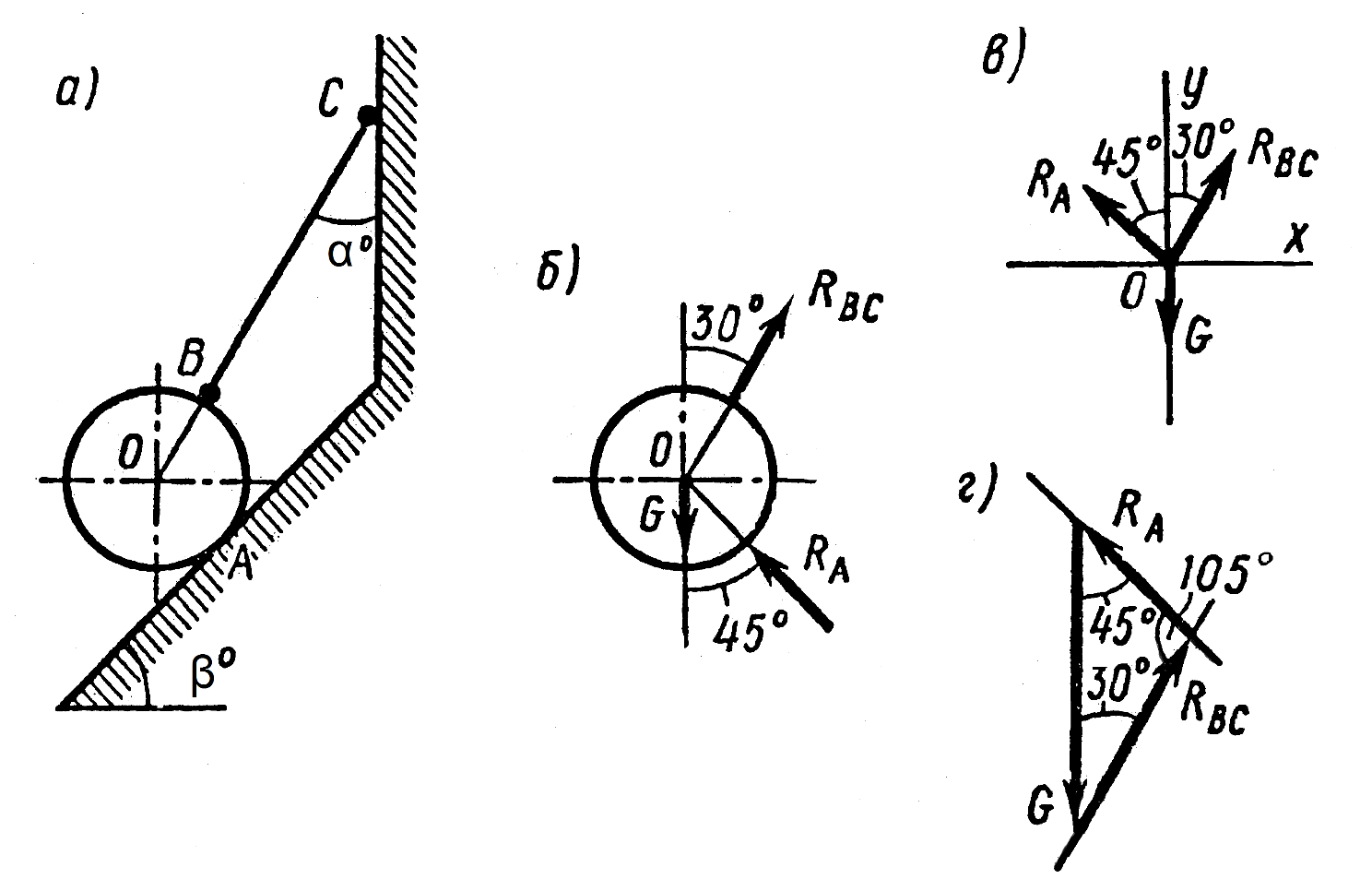
Определить силу натяжения троса, удержи­вающего в равновесии шар весом G = 20 Н, а также силу давления шара на наклонную опорную плоскость, если α = 30°, β = 45°.

Задачу решаем аналитическим методом. К шару приложена заданная активная сила — вес шара G. Отбрасываем связи (трос ВС и опорная плоскость), заменяя их действие реакциями R_BC и R_A. Реакцию растянутого троса направляем от шара, а реакцию опорной плоскости — по нормали к ней в сторону к шару.

Рассматриваем равновесие точки O схода всех сил. Полученная расчет­ная схема изображена на рис.б.

Принимаем обычное вертикально-горизонтальное направление координатных осей (рис. в). Для полученной плоской системы сходящихся сил составляем два уравнения равновесия:

 

1) ∑F_X= 0; R_BCcos60° - R_Acos 45° = 0;

R_BC0,5 - R_A0,707= 0;

2) ∑ F_Y= 0; R_BCcos30° + R_Acos 45° - G = 0;

R_BC0,866 +R_A 0,707 - 20 = 0;

 

Решая полученную систему уравнений, находим:R_A= 10,3 Н и R_BC=14,6Н. Искомая сила натяжения троса и сила давления шара на плоскость соответственно равны найденным реакциям, а по направ­лению противоположны им.

Для проверки правильности решения применяем графоаналитиче­ский метод - строим замкнутый силовой треугольник (рис. г). От произвольной точки откладываем вектор заданной силы G, через начало и конец которого проводим известные направления искомых реакций троса и опоры. Построенный графическим методом силовой треугольник решаем аналитическим методом — здесь удобно применить известную из математики теорему синусов:

G /sin105° = R_BC/sin45° =R_A /sin 30°;

20/0,967 = R_BC/ 0,707 = R_A / 0,5.

Решая пропорции, получаем

R_BC= 20 ∙ 0,707/0,967 =14,6 кН;

R_A = 20 ∙0,5/0,967 = 10,3 кН.

 

 

Контрольные вопросы.

1. Перечислить основные виды (модели) связей, показать направле­ния их реакций.

2. Дайте определение сходящейся системы сил.

3. Изложите правило построения силового многоугольника.

4. Как определить значение и знак проекции силы на ось координат?

5. Сколько и каких уравнений можно составить при рассмотрении
равновесия плоской системы сходящихся сил?

6. В чем состоит аналитический способ нахождения равнодействующей сходящихся сил на плоскости?

7. Найти углы, составляемые силами F1 = 2,5 кН и F2 = 2,0 кН с равнодействующей R = 3,5 кН.

8. Найти равнодействующую R двух сил: F1 = 50 Н и F2 = 25 Н если угол между их векторами равен 135°. Решение провести аналитически и графически. Результаты сравнить.

9. В каком случае проекция силы на ось равна нулю?

г

 

 

Литература.

 

Аркуша А.И. Техническая механика: Теоретическая механика и сопротивление материалов: Учебник для машиностроительных специализированных техникумов.- 2-е изд., доп.-М.: Высшая школа, 2008.- 352 с., ил.