Для заданного сечения, составленного из прокатных профилей двух швеллеров и полосы, определитьположение центра тяжести.
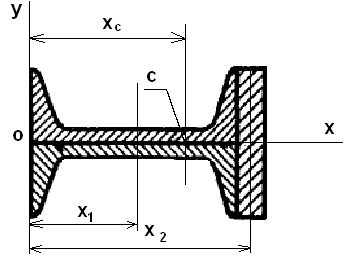
Данное сечение состоит из двух швеллеров №24 и полосы 16 х 180 мм. Геометрические характеристики сечения швеллера находим из сортамента ГОСТ 8240-97. Фигура имеет ось симметрии. Центр тяжести лежит на этой оси. Совмещаем ее с осью X. Начало координат – в левом крае сечения. Координата центра тяжести сечения по оси Y: yc= 0. Координата центра тяжести сечения по оси X:
xc = (2· A1 · x1 + A2 · x2)/ (2 · A1 + A2) =
= (2 · 30,6 · 12 + 28,8 · 24,8)/ (2 · 30,6 + 28,8) = 16,1 см, где
А1 = 30,6 cм2 – площадь сечения швеллера №24 из сортамента
x1 = h/2 = 24/2= 12cм – координата x центра тяжести сечения швеллера №24
h = 24 см – высота швеллера № 24
A2 = 1,6 · 18 = 28,8 см2 – площадь сечения полосы
x2 = h + 1,6 /2 = 24 + 0,8 = 24,8 см –координата xцентра тяжести полосы.
Контрольные вопросы.
1. Является ли центр тяжести тела центром параллельных сил?
2. Где находится центр тяжести тела, имеющего ось симметрии,
центр симметрии? Привести примеры.
3 Изменится ли положение центра тяжести тела от поворота его на некоторый угол?
4. Как найти координаты центра тяжести треугольника и круга?
Плоского составного сечения?
Литература.
Аркуша А.И. Техническая механика: Теоретическая механика и сопротивление материалов: Учебник для машиностроительных специализированных техникумов.- 2-е изд., доп.-М.: Высшая школа, 2008.- 352 с., ил.
Практическое занятие №4.
Решение задачи по трению скольжения.
Цель работы.
Используя законы сухого трения при скольжении, научится вести расчёты предельного равновесного состояния систем с реальными связями (связями с трением).
Задание.
На барабан радиуса r насажен тормозной шкив радиуса R = 2r. С барабана сбегает трос, к концу которого подвешен груз Q. К шкиву с помощью рычага DAB прижимается тормозная колодка K. Определить силу F, которую необходимо приложить к рычагу DAB чтобы удержать барабан от вращения, если коэффициент трения между тормозной колодкой и тормозным шкивом равен ƒ. Весом рычага DAB, а также размерами колодки пренебречь. Значения параметров для расчёта принять из таблицы для своего варианта.
| № вар. | Q, Н | a, м | b, м | c, м | f | № вар. | Q, Н | a, м | b, м | c, м | f |
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,6 | 0,6 | 0,4 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 | ||||
| 0,7 | 0,8 | 0,8 | 0,35 | 0,4 | 0,5 | 0,5 | 0,45 |
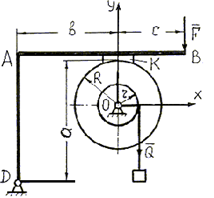
Рассматриваемая конструкция состоит из двух тел. Возможными объектами равновесия является конструкция в целом, рычаг DAB с колодкой и барабан со шкивом.
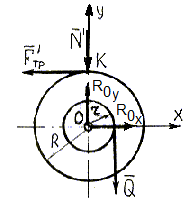
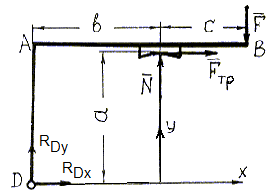
Для решения задачи достаточно рассмотреть два каких-либо объекта из трех.
Первый объект - барабан со шкивом.На него действуют три неизвестные силы: Royи Rox– проекции на оси Yи X реакции отброшенной опоры (подшипника) вала барабана и шкива; Nʹ - сила давления колодки на тормозной шкив. Столько же можно составить уравнений равновесия.
Вторым объектом может быть либо рычаг DAB, либо конструкция в целом. Возмем за объект рычаг DAB с колодкой, так как на него действует меньше сил, чем на конструкцию в целом.
Запишем уравнения равновесия сил, приложенных к барабану со шкивом:
∑Fx= 0; Rox- Fʹтр= 0.
∑Fy= 0; Roy- Nʹ -Q= 0.
∑ Mо(Fi) = 0; Fʹтр ∙ 2r –Q ∙r= 0.
Из последнего уравнения при Q= 200Н:
Fʹтр= Q ∙r/(2r) = Q/2 =200/2 = 100Н.
В предельном состоянии равновесия Fʹтр=f∙Nʹ. Тогда при f = 0,4:
Nʹ = Fʹтр/f = 100/0,4 = 250Н.
Далее рассмотрим равновесие рычага DAB, на который действуют следующие силы: F– активная сила, величину которой следует определить; RD– реакция шарнира D; N– реакция шкива, Fтр– сила трения. Учтем, что по закону равенства действия и противодействия N = - Nʹ; Fтр= - Fʹтр.
Для определения силы F достаточно составить одно уравнение равновесия:
∑ MD(Fi) = 0; - F ∙ (b + c) – Fтр ∙ a + N∙ b = 0.
При a = 0,4м; b = 0,5м; с = 0,5м получим F = 85Н.
.