a. числами степеней свободы m и n
b. числом степеней свободы n
c. числом степеней свободы n-m
31. В экономике чаще всего большинство случайных величин задается в виде:
a. закрытых случайных величин
b. непрерывных случайных величин
32. Заключительным этапом эконометрических исследований является:
a. интерпретация результатов
b. получение данных и анализ их качества
c. оценка параметров
d. спецификация модели
33. Если коэффициент корреляции между двумя случайными величинами больше нуля, то значит:
a. случайные величины имеют прямую линейную зависимость
b. случайные величины имеют обратную линейную зависимость
c. случайные величины не зависимы
34. Альтернативной называется:
a. гипотеза, необходимая для проверки нулевой гипотезы
b. гипотеза, которая отклоняется
c. гипотеза, которая содержит несколько конкретных предположений
35. Случайным называется такое событие, которое:
a. может произойти или не произойти в условиях данного эксперимента
b. не происходит никогда в условиях данного эксперимента
c. происходит всегда в условиях данного эксперимента
36. Способы уменьшения вероятности ошибок при проверке статистических гипотез состоят в:
a. минимизации потерь от ошибок
b. уменьшении вероятностей ошибок
c. увеличении объема выборки
37. Средние расходы домохозяйств в расчете на одну потребительскую единицу составляли, ден. ед. в месяц: на питание – 62 при σ=9,3, на одежду и обувь – 26 при σ=9,1. Степень вариации расходов на питание и покупку одежды и обуви:
a. одинакова
b. вариация расходов на питание больше
c. вариация расходов на питание меньше
38. Установите правильное соответствие:
a. 1-2, 2-1, 3-4
b. 1-2,2-3, 3-4
c. 1-3,2-1,3-2
39. Пространственными данными является:
a. набор сведений по разным объектам наблюдения, взятым за один и тот же период или момент времени
b. набор сведений, характеризующий один и тот же объект, но за разные периоды или моменты времени
c. набор сведений по разным объектам наблюдения за разные периоды или моменты времени
40. Укажите правильную последовательность этапов эконометрического моделирования:
a.выбор общего вида модели (спецификация),
b. оценка параметров модели (идентификация),
c. определение конечных целей модели,
d. сбор информации, анализ ее качеств,
41. Достоверным называется такое событие, которое:
a. происходит всегда в условиях данного эксперимента
b. может произойти или не произойти в условиях данного эксперимента
c.не происходит никогда в условиях данного эксперимента
42. Средний уровень жизни Х и Y двух стран (США и Англии соответственно) примерно одинаковы, но разброс в доходах этих стран различны. За последние двадцать лет получены следующие результаты:
Sx2 =300; Sy2 = 120. На основании выборочных данных можно утверждать, что:
a. на уровне значимости α=0,1 и 0,05 разброс в доходах в США больше, чем в Англии
b. на уровне значимости α=0,01 разброс в доходах США больше, чем в Англии
c.на любом уровне значимости нет оснований утверждать, что разброс в доходах в США больше, чем в Англии
43 Оцените качество построенной модели, не прибегая к таблицам, совпадает ли направление влияния объясняющих переменных с теоретическим?
a. качество модели высокое, направление влияния совпадает
b. качество модели низкое, направление влияния совпадает
c. качество модели высокое, но направление влияния не совпадает
d. качество модели низкое, направление влияния совпадает
44. Критерий Стьюдента предназначен для:
a. Определения экономической значимости каждого коэффициента уравнения
b. Определения статистической значимости каждого коэффициента уравнения
c. Проверки модели на автокорреляцию остатков
d. Определения экономической значимости модели в целом
45. Остаточная сумма квадратов отклонений отражает влияние на разброс у:
a. изучаемого фактора х
b. прочих факторов
c. изучаемого фактора х и прочих факторов
46. Если фактор не оказывает влияния на результат, то линия регрессии на графике:
a. параллельна оси ох
b. параллельна оси оу
c. является биссектрисой первой четверти декартовой системы координат
47. Общая сумма квадратов отклонений совпадает с остаточной, когда:
a. фактор х не оказывает влияния на результат
b. прочие факторы не влияют на результат
c. фактор х и прочие факторы в равной степени влияют на результат
48. Остаточная сумма квадратов отклонений в парной регрессии имеет число степеней свободы, равное:
a. n-2
b. 
c. 
d. 
49. Эмпирический коэффициент регрессии b является несмещенной оценкой 
если:
a. 
b. 
c. 
50. Графический метод подбора вида уравнения регрессии основан на:
a. поле корреляции
b. математической природе связи
с. равнении остаточной дисперсии для разных моделей
51. Аналитический метод подбора вида уравнения регрессии основан на:
a. поле корреляции
b. математической природе связи
c. сравнении остаточной дисперсии для разных моделей
52. Если свободный коэффициент в уравнении регрессии больше нуля, то:
a. вариация результата меньше вариации фактора
b. вариация результата больше вариации фактора
c. относительное изменение результата происходит быстрее, чем изменение фактора
53. Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом: 
Сравнить эластичности затрат по каждому виду продукции при x=50 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
a. 
b. 
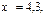
c. 
d. 
54. Дана следующая модель спроса и предложения:
Спрос: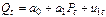 
, 
;
Предложение: 
, 
:
a. данная модель точно идентифицируема
b. данная модель сверхидентифицируема
c. данная модель неидентифицируема
55. Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -0,31 + 1,5 x t + 3 x t-1 + 4,5 x t-2 + 0,5 x t-3
Краткосрочный, долгосрочный мультипликатор и средний лаг равны:
a. краткосрочный 0,5, долгосрочный 9,2, средний лаг 2,3
b. краткосрочный 1,5, долгосрочный 9,5, средний лаг 0,791
c. краткосрочный -0,67, долгосрочный
Примерные вопросы для подготовки
к зачету
Предмет, задачи, критерии и принципы эконометрики.
1. Типы моделей, используемые для анализа и прогноза экономических процессов.
2. Метод наименьших квадратов.
3. Основные эконометрические методы.
4. Построение модели парной регрессии.
5. Теорема Гаусса - Маркова.
6. Построение модели множественной регрессии.
7. Оценка коэффициентов линейной регрессии.
8. Коэффициент корреляции.
9. Коэффициент детерминации.
10. Мультиколлинеарность. Тесты на наличие мультиколлинеарности.
11. Тесты на устранение мультиколлинеарности.
12. Гомогедастичность и гетероскедастичность. Тесты на наличие гетероскедастичности
13. Тесты на устранение гетероскедастичности.
14. Фиктивные переменные. Критерий Чоу.
15. Временные ряды. Стационарные и нестационарные временные ряды.
16. Автокорреляция остатков временного ряда. Тесты на наличие автокорреляции.
17. Устранение автокорреляции.
18. Понятие об авторегрессионных моделях.
19. Модели скользящей средней.
20. Метод инструментальных переменных.
21. Оценивание моделей с распределенными лагами.
22. Системы одновременных уравнений.
23. Двухшаговый метод наименьших квадратов.
24. Трехшаговый метод наименьших квадратов.
Литература
Основная:
1. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс. Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 1997. – 245 с.
2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2007. – 402 с.
Дополнительная:
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: Юнити, 1998. – 1022 с.
2. Многомерный статистический анализ в экономике / Под ред. В.Н. Тамашевича. – М.: Юнити-Дана, 1999. – 598 с.
3. Айвазян С.А., Енюков Й.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, 1983.
4. Айвазян С.А., Енюков Й.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей. – М.: Финансы и статистика, 1985.
5. Айвазян С.А., Бухштабер В.М., Енюков С.А., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. – М.: Финансы и статистика, 1989.
6. Бард Й. Нелинейное оценивание параметров. – М.: Статистика, 1979.
7. Демиденко Е.З. Линейная и нелинейная регрессия. – М.: Финансы и статистика, 1981.
8. Джонстон Д. Эконометрические методы. – М.: Статистика, 1980.
9. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. В 2-х кн. – М.: Финансы и статистика, 1986.
10. Себер Дж. Линейный регрессионный анализ. – М.: Мир, 1980.
11. Андерсон Т. Cтатистический анализ временных рядов. – М.: Мир, 1976.
12. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. (Вып. 1, 2). – М.: Мир, 1972.
13. Дженкинс Г., Ваттс Д. Cпектральный анализ и его применения. – М.: Мир, 1971.
14. Гренджер К., Хатанака М. Cпектральный анализ временных рядов в экономике. – М.: Статистика, 1972.
15. Кендэл М. Временные ряды. – М.: Финансы и статистика, 1981.
16. Вапник В.Н. Восстановление зависимостей по эмпирическим данным. – М.: Наука, 1979.
17. Дюран Б., Оделл П. Кластерный анализ. – М.: Статистика, 1977.
18. Ермаков C.М., Жиглявский А.А. Математическая теория оптимального эксперимента. – М.: Наука, 1982.
19. Лоули Д., Максвелл А. Факторный анализ как статистический метод. – М.: Мир, 1967.
20. Розин Б.Б. Теория распознавания образов в экономических исследованиях. – М.: Статистика, 1973.
21. Справочник по прикладной статистике. – М.: Финансы и статистика, 1990.
22. Хьюбер П. Робастность в статистике. – М.: Мир, 1984.
23. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980.
Приложение
Глоссарий
(Основные термины и определения)
1. Уравнение Y t = b 0 + b 1 X t + e t , t = 1,….,n, где
X t -неслучайная (детерминированная) величина,
Yt, b 0 и b 1 – неизвестные параметры,
e t -случайные величины, называется линейным регрессионным уравнением.
Yt называется объясняемой (зависимой) переменной, а Xt - объясняющей (независимой) переменной или регрессором
2. Основные гипотезы:
1. Y t = b 0 + b 1 X t + e t , t = 1,….,n, - спецификация модели.
2. X t - детерминированная величина;
3. e i - случайная величина, удовлетворяющая следующим предпосылкам
3а) Ee t = 0, (ЕY t =b 0 + b 1 X t), E (e t2) = V(e t) = s 2, (V(Y t) = s 2) - не зависит от t.
3б) E(e t e s) = 0 (Cov (Y t, Y s)=0), t ¹ s - некоррелированность ошибок для разных наблюдений.
Часто добавляется условие:
3в) e t ~ N(0, s 2), т.е. e t - нормально распределенная случайная величина со средним 0 и дисперсией s 2.
Условие независимости дисперсии ошибки от номера наблюдений E (e t2) = s 2, t = 1,….,n, называется гомоскедастичностью (а); случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью (б).
Теорема Гаусса - Маркова.
Для модели 1 -3ab:
оценки b 0, b 1 параметров регрессии, полученные по методу наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок s 2.
3. Коэффициент детерминации.
Q - вся дисперсия, Qe - остаточная дисперсия, QR - объясненная часть всей дисперсии.
Коэффициентом детерминации R 2 или долей объясненной дисперсии называется
R 2 = 1 - 
= 
.
4. Классическая нормальная линейная модель множественной регрессии.
Модель множественной регрессии:
y i = b 0 + b 1 x i1 + b 2 x i3 + b p x i p + e i i = 1,2, … n;
где х tp - значения регрессора х p в наблюдении t.
Основные гипотезы, лежащие в основе модели множественной регрессии, являются естественным обобщением модели парной регрессии:
1. yi = b0 + b1 xi1 + b2 x i3 + b p x i p + e i i = 1,2, … n;
- спецификация модели.
2. xi1, x i2,…. x i p - детерминированные величины. Векторы х s = (x1s, …. xns)', s = 1,….p линейно независимы в R n.
3. ei - случайная величина, удовлетворяющая следующим предпосылкам:
3a) Е(e i) = 0; D (e i) = s 2 для любого i;
3б) e i и e j не коррелированы: Е(e i, e j) = 0 при i ¹ j; выводится из условия некоррелированности Cov (e i, e j) = 0; (Cov (e i, e j) = Е[(e i - 0) ((e j - 0)]) = Е(e i, e j) = 0).
Часто добавляется условие:
3в) e t ~ N(0, s 2), т.е. et - нормально распределенная случайная величина со средним 0 и дисперсией s 2.
В этом случае модель называется нормальной линейной регрессионной.
Все эти условия удобно записать в матричной форме:
У = Х × b + e
или
у i = b 0 + 
+ e i, i = 1,2,….n.
где У = (у 1,…у n) ' - вектор значений зависимой переменной;
- матрица значений объясняющих переменных, в которую дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что модели (МР1) свободный член b 0 умножается на фиктивную переменную х i 0, принимающую значение 1 для всех i:
х i 0 =1 (i = 1,2,….n);
b = (b 0, b1, …… b p)' - вектор параметров размера (р + 1); e = (e 1,e 2,…. e n) – вектор возмущений (случайных ошибок) размера n.
Теорема Гаусса - Маркова.
Предположим, что:
1. у = Х b + e;
2. Х - детерминированная n ´ (p+1) матрица, имеет максимальный ранг (p+1);
3. Е(e) = 0; Е(e e ') = s 2 1 n.
4. e - нормально распределенный случайный вектор e ~ N(0, s 21 n);
5. r (X) = p + 1 < n
Тогда при выполнении предпосылок (1-3, 5) оценка МНК b = (X' X)- 1 X' y является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных (по у) несмещенных оценок.
5. Ковариационная матрица и ее выборочная оценка.
Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их вычисления используют ковариационную матрицу вектора оценок параметров å b.
å b = 
,
где sij2 - ковариации (корреляционные моменты) оценок параметров bi и bj.
s ij 2 = Е[ (b i - Е(b i))(b j - Е(b j))]. (МР7)
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
Оценка дисперсии ошибок s 2. Распределение s 2.
S 2 = 
= 
является несмещенной оценкой дисперсии ошибок (возмущений) s 2, т.е. Еs 2 = s 2.
6. Оценка значимости коэффициентов регрессии b j.
Значимость коэффициентов регрессии b j можно проверить, если учесть, что статистика (b j - b j0)/ s b j имеет t - распределение Стьюдента с к = n - p - 1 степенями свободы. Поэтому b j значимо отличается от нуля (т.е. гипотеза Н 0 о равенстве параметра b j нулю Н 0: b j0 = 0, отвергается) на уровне значимости a, если 
, где t 1 - a; n - p -1 - табличное значение t - критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы к = n - p - 1.
7. Доверительный интервал для параметра b j есть
b j - t 1 - a; n - p -1 s b j £ b j £ b j + t 1 - a; n - p -1 s b
8. Доверительный интервал для функции регрессии или для условного математического ожидания зависимой переменной Е х(У):
- t 1 - a; k 
< Е(Y) < + t 1 - a; k
где - групповая средняя, определяемая по уравнению регрессии,
= 
- ее стандартная ошибка.
9. Доверительный интервал для индивидуальных значений зависимой переменной у *0 примет вид:
- t 1 - a; n - p -1 
< у *0 < + t 1 - a; n - p - 1 ,
где = 
.
10. Доверительный интервал для параметра s 2 в множественной регрессии:
.
11. Оценка значимости уравнения регрессии.
Проверить значимость уравнения регрессии - значит установить, соответствует ли математическая модель, выражающая зависимость между переменными и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
При отсутствии линейной зависимости между зависимой переменной и объясняющей переменными несмещенные оценки дисперсий
s2R = QR/(m - 1) и s2e = Qe/(n - m) имеют c 2 -распределение с соответственно к = m-1 и к = n-m степенями свободы, а их отношение - F -распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики
F = 
> Fa; k1;k2,
где Fa; k1;k2 - табличное значение F - критерия Фишера - Снедекера, определенное на уровне значимости a при к 1 = m - 1 и к 2 = n - m степенях свободы.
Значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
12. Оценка значимости коэффициента корреляции при отсутствии корреляционной связи статистика t = 
имеет распределение Стьюдента с (n - 2) степенями свободы. Коэффициент корреляции r значим на уровне a (т.е. гипотеза Н0 о равенстве генерального коэффициента корреляции r = 0 отвергается), если
½ t½ = 
> t 1 - a; n - 2.
13. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.
14. Автокорреляции ошибок, если E(e t e s) = r ¹ 0,
15. Стандартизированные коэффициенты регрессии b'j и коэффициенты эластичности Е j (j = 1,….p):
b'j = 
;
E j = 
.
Стандартизированный коэффициент регрессии b'j показывает, на сколько величин sy изменится в среднем зависимая переменная У при увеличении только j -ой объясняющей переменной на sxj, а коэффициент эластичности Е j - на сколько процентов (от средней) изменится в среднем У при увеличении только Х j на 1 %.
16. Временным рядом (динамическим рядом или рядом динамики) в экономике называется последовательность наблюдений некоторого признака (случайной величины) У в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые обозначаются у t (t = 1,2,….n), где n - число уровней.
В общем виде при исследовании экономического временного ряда у t выделяются несколько составляющих:
у t = u t + n t + c t + e t t = 1,2,….n,
где u t - тренд,
n t - сезонная компонента,
c t - циклическая компонента,
e t - случайная компонента,
u t, n t, c t - закономерные, неслучайные составляющие.
17. Стационарные временные ряды.
Временной ряд у t (t=1,2,…,n) называется строго стационарным, если совместное распределение вероятностей n наблюдений у 1, у 2,…..уn такое же, как и n наблюдений у 1 + t, у 2 + t,…у n + t при любых n, t и t, т.е. свойства строго стационарных рядов у t (закон распределения и его числовые характеристики) не зависят от момента t.
18. Степень тесноты связи между последовательностями наблюдений временного ряда у 1, у 2,…у n и у 1 + t, у 2 + t,….у n + t (сдвинутых относительно друг друга на t единиц, т.е. с лагом t) может быть определена с помощью коэффициента корреляции
так как Е(у t) = Е(у t + t) = a, s y(t) = s y(t + t) = s.
Так как коэффициент r(t) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость r(t) - автокорреляционной функцией. В силу стационарности временного ряда у t автокорреляционная функция r(t) зависит от лага t, причем r(- t) = r(t), т.е. при r(t) можно ограничиться рассмотрением только положительных значений t.
19. Статистической оценкой r(t) является выборочный коэффициент автокорреляции r(t), определяемый по формуле
r(t) = 
.
Функцию r(t) называют выборочной автокорреляционной функцией, а ее график - коррелограммой.
Приложение 2
Критические значения критерия F (Фишера)
для уровней статистической значимости р < 0,05 и р < 0,01:
df1 - число степеней свободы в числителе,
df2 - число степеней свободы в знаменателе
(по Snedecor., 1956)
Таблица 1
| ||||||||||||
| P = 0.05 | ||||||||||||
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 | 19,40 | 19,41 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 | 8,76 | 8,74 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | 5,93 | 5,91 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,78 | 4,74 | 4,70 | 4,68 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | 4,03 | 4,00 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,63 | 3,60 | 3,57 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,34 | 3,31 | 3,28 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,13 | 3,10 | 3,07 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 | 2,94 | 2,91 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,86 | 2,82 | 2,79 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 | 2,80 | 2,76 | 2,72 | 2,69 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 | 2,72 | 2,67 | 2,63 | 2,60 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 | 2,65 | 2,60 | 2,56 | 2,53 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,70 | 2,64 | 2,59 | 2,55 | 2,51 | 2,48 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,45 | 2,42 | |
| P = 0.01 | ||||||||||||
| 98,49 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,36 | 99,37 | 99,39 | 99,40 | 99,41 | 99,42 | |
| 34,12 | 30,82 | 29,46 | 28,71 | 28,24 | 27,91 | 27,67 | 27,49 | 27,34 | 27,23 | 27,13 | 27,05 | |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,98 | 14,80 | 14,66 | 14,54 | 14,45 | 14,37 | |
| 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,45 | 10,29 | 10,15 | 10,05 | 9,96 | 9,89 | |
| 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,26 | 8,10 | 7,98 | 7,87 | 7,79 | 7,72 | |
| 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 7,00 | 6,84 | 6,71 | 6,62 | 6,54 | 6,47 | |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,19 | 6,03 | 5,91 | 5,82 | 5,74 | 5,67 | |
| 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,62 | 5,47 | 5,35 | 5,26 | 5,18 | 5,11 | |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,21 | 5,06 | 4,95 | 4,85 | 4,78 | 4,71 | |
| 9,65 | 7,20 | 6,22 | 5,67 | 5,32 | 5,07 | 4,88 | 4,74 | 4,63 | 4,54 | 4,46 | 4,40 | |
| 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,65 | 4,50 | 4,39 | 4,30 | 4,22 | 4,16 | |
| 9,07 | 6,70 | 5,74 | 5,20 | 4,86 | 4,62 | 4,44 | 4,30 | 4,19 | 4,10 | 4,02 | 3,96 | |
| 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,28 | 4,14 | 4,03 | 3,94 | 3,86 | 3,80- | |
| 8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,14 | 4,00 | 3,89 | 3,80 | 3,73 | 3,67 | |
| 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 4,03 | 3,89 | 3,78 | 3,69 | 3,61 | 3,55 |
Таблица 1. Продолжение
| df1 | ||||||||||||
| df2 | P = 0.05 | |||||||||||
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,62 | 2,55 | 2,50 | 2,45 | 2,41 | 2,38 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 3,66 | 2,58 | 2,51 | 2,46 | 2,41 | 2,37 | 2,34 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2.55 | 2,48 | 2,43 | 2,38 | 2,34 | 2,31 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,52 | 2,45 | 2,40 | 2,35 | 2,31 | 2,28 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,49 | 2,42 | 2,37 | 2.32 | 2,28 | 2,25 | |
| 4.30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,47 | 2,40 | 2,35 | 2,30 | 2,26 | 2,23 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,45 | 2,38 | 2,32 | 2,28 | 2,24 | 2,20 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,43 | 2,36 | 2,30 | 2,26 | 2,22 | 2,18 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,41 | 2,34 | 2,28 | 2,24 | 2,20 | 2,16 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 | 2,27 | 2,22 | 2,18 | 2,15 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,37 | 2,30 | 2,25 | 2,20 | 2,16 | 2,13 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,36 | 2,29 | 2,24 | 2,19 | 2,15 | 2,12 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,35 | 2,28 | 2,22 | 2,18 | 2,14 | 2,10 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,34 | 2,27 | 2,21 | 2,16 | 2,12 | 2,09 | |
| 4,15 | 3,30 | 2,90 | 2,67 | 2,51 | 2,40 | 2,32 | 2,25 | 2,19 | 2,14 | 2,10 | 2,07 | |
| 4,13 | 3,28 | 2,88 | 2,65 | 2,49 | 2,38 | 2,30 | 2,23 | 2,17 | 2,12 | 2,08 | 2,05 | |
| P = 0.01 | ||||||||||||
| 8,40 | 6,11 | 5,18 | 4,67 | 4,34 | 4,10 | 3,93 | 3,79 | 3,68 | 3,59 | 3,52 | 3,45 | |
| 8,28 | 6,01 | 5,09 | 4,58 | 4,25 | 4,01 | 3,85 | 3,71 | 3,60 | 3,51 | 3,44 | 3,37 | |
| 8,18 | 5,93 | 5,01 | 4,50 | 4,17 | 3,94 | 3,77 | 3,63 | 3,52 | 3,43 | 3,36 | 3,30 | |
| 8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,71 | 3,56 | 3,45 | 3,37 | 3,30 | 3,23 | |
| 8,02 | 5,78 | 4,87 | 4,37 | 4,04 | 3,81 | 3,65 | 3,51 | 3,40 | 3,31 | 3,24 | 3,17 | |
| 7,94 | 5,72 | 4,82 | 4,31 | 3,99 | 3,76 | 3,59 | 3,45 | 3,35 | 3,26 | 3,18 | 3,12 | |
| 7,88 | 5,66 | 4,76 | 4,26 | 3,94 | 3,71 | 3,54 | 3,41 | 3,30 | 3,21 | 3,14 | 3,07 | |
| 7,82 | 5,61 | 4,72 | 4,22 | 3,90 | 3,67 | 3,50 | 3,36 | 3,25 | 3,17 | 3,09 | 3,03 | |
| 7,77 | 5,57 | 4,68 | 4,18 | 3,86 | 3,63 | 3,46 | 3,32 | 3,21 | 3,13 | 3,05 | 2,99 | |
| 7,72 | 5,53 | 4,64 | 4,14 | 3,82 | 3,59 | 3,42 | 3,29 | 3,17 | 3,09 | 3,02 | 2,96 | |
| 7,68 | 5,49 | 4,60 | 4,11 | 3,79 | 3,56 | 3.39 | 3,26 | 3,14 | 3,06 | 2,98 | 2,93 | |
| 7,64 | 5,45 | 4,57 | 4,07 | 3,76 | 3,53 | 3,36 | 3,23 | 3,11 | 3,03 | 2,95 | 2,90 | |
| 7,60 | 5,42 | 4,54 | 4,04 | 3,73 | 3,50 | 3,33 | 3,20 | 3,08 | 3,00 | 2,92 | 2,87 | |
| 7,56 | 5,39 | 4.51 | 4,02 | 3,70 | 3,47 | 3,30 | 3,17 | 3.06 | 2,98 | 2,90 | 2,84 | |
| 7,50 | 5,34 | 4,46 | 3,97 | 3,66 | 3,42 | 3,25 | 3,12 | 3,01 | 2,94 | 2,86 | 2,80 | |
| 7,44 | 5,29 | 4,42 | 3,93 | 3,61 | 3,38 | 3,21 | 3,08 | 2,97 | 2,89 | 2,82 | 2,76 |
Таблица 1. Продолжение
| df2 | ||||||||||||
| df1 | P = 0.05 | |||||||||||
| 4,11 | 3,26 | 2,86 | 2,63 | 2,48 | 2,36 | 2,28 | 2,21 | 2,15 | 2,10 | 2,06 | 2,03 | |
| 4,10 | 3,25 | 2,85 | 2,62 | 2,46 | 2,35 | 2,26 | 2,19 | 2,14 | 2,09 | 2,05 | 2,02 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | 2,07 | 2,04 | 2,00 | |
| 4,07 | 3,22 | 2,83 | 2,59 | 2,44 | 2,32 | 2,24 | 2,17 | 2,11 | 2,06 | 2,02 | 1,99 | |
| 4,06 | 3,21 | 2,82 | 2,58 | 2,43 | 2,31 | 2,23 | 2,16 | 2,10 | 2,05 | 2,01 | 1,98 | |
| 4,05 | 3,20 | 2,81 | 2,57 | 2,42 | 2,30 | 2,22 | 2,14 | 2,09 | 2,04 | 2.00 | 1,97 | |
| 4,04 | 3,19 | 2,80 | 2,56 | 2,41 | 2,30 | 2,21 | 2,14 | 2,08 | 2,03 | 1,99 | 1,96 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2.40 | 2,29 | 2,20 | 2,13 | 2,07 | 2,02 | 1,98 | 1,95 | |
| 4,02 | 3,17 | 2,78 | 2,54 | 2,38 | 2,27 | 2,18 | 2,11 | 2,05 | 2,00 | 1,97 | 1,93 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | 1,99 | 1,95 | 1,92 | |
| 3,99 | 3,14 | 2,75 | 2,51 | 2,36 | 2,24 | 2,15 | 2,08 | 2,02 | 1,98 | 1,94 | 1,90 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,14 | 2,07 | 2,01 | 1,97 | 1,93 | 1,89 | |
| 3,96 | 3,11 | 2,72 | 2,48 | 2,33 | 2,21 | 2,12 | 2,05 | 1,99 | 1,95 | 1,91 | 1,88 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,10 | 2,03 | 1,97 | 1,92 | 1,88 | 1,85 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,08 | 2,01 | 1,95 | 1,90 | 1,86 | 1,83 | |
| 3,91 | 3,06 | 2,67 | 2,43 | 2,27 | 2,16 | 2,07 | 2,00 | 1,94 | 1,89 | 1,85 | 1,82 | |
| 3,89 | 3,04 | 2,65 | 2,41 | 2,26 | 2,14 | 2,05 | 1,98 | 1,92 | 1,87 | 1,83 | 1,80 | |
| 3,86 | 3,02 | 2,62 | 2,39 | 2,23 | 2,12 | 2,03 | 1,96 | 1,90 | 1,85 | 1,81 | 1,78 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-16 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |