Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
Под фигурой Ω будем понимать ограниченное замкнутое тело с вкл. гран. Множ. Диаметр d фигурыΩ будем называть максимальное из расстояний между двумя точками этой фигуры. Для эллипса – большая ось. Под мерой ω для плоской фигуры и поверхности будем понимать площадь S, для линии – длину линии, для пространственного тела объём.
Определённый интеграл по фигуре Ω от заданной на ней функции f(p) называется предел n-интегральной суммы, когда  . В случае когда фигура плоск. обл.Д, интеграл называется двойным.
. В случае когда фигура плоск. обл.Д, интеграл называется двойным.
Масса фигуры переменной плотности
. Масса фигуры (отрезка, дуги, плоской фигуры, части криволинейной поверхности, тела)
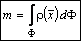 ,
,
если подынтегральная функция 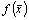 ,
,  , задает
, задает
плотность 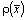 линейная
линейная 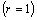 распределения поверхностная (
распределения поверхностная ( )
)
массы по 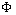 объемная (
объемная (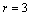 )
)
в зависимости от размерности фигуры,  ,
,  ,
, 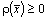
на 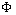 .
.
Геометрический смысл ДИ (двойного интеграла)
Вычислим V цилиндрического тела. Сверху ограниченного поверхностью z=f(x,y) проекция поверхности на плоскость xoy =>область Д и цилиндр. образующ. кот. // oz
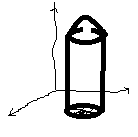 Разобьем область Д на n-цилиндрических тел основаниями которых будут элементы области ∆
Разобьем область Д на n-цилиндрических тел основаниями которых будут элементы области ∆ 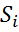 . Возьмём произвольную точку
. Возьмём произвольную точку 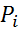 в области ∆
в области ∆ 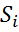 и h-z=f (
и h-z=f (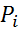 ), тогда ∆
), тогда ∆ 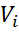 =f(
=f(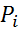 )* ∆
)* ∆ 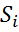 , a V ≈
, a V ≈ 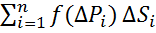 =>
=>
V= 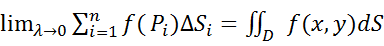
Двойной интеграл – V цилиндрического тела с основанием Д ограниченного сверху поверхностью z=f(x,y)
Замечания: 1. Если объём ограниченный сверху z=f(x,y), снизу z=f1(x,y), то V= 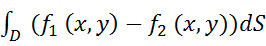
2. Если f(x,y)≤0 неопред. в области Д, то ДИ от этой функции = V цилиндрического тела взятому со знаком «-»
Геометрический смысл Кр И -1
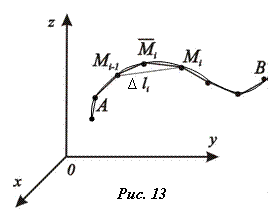
1. Дугу кривой 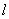 или или 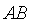 в пространстве XOYZ разбиваем на n малых частей точками M 0= A, M 1,…, Mn = B; обозначаем длины хорд в пространстве XOYZ разбиваем на n малых частей точками M 0= A, M 1,…, Mn = B; обозначаем длины хорд 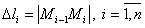 , (Рис. 13) , (Рис. 13)
| 
|
2. Вычисляем значения функции f (x, y, z) в произвольно выбираемых точках  на i -той части разбиения и умножаем их на соответствующие длины хорд Δ li:
на i -той части разбиения и умножаем их на соответствующие длины хорд Δ li: 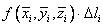 ,
, 
3. Составляем интегральную сумму

и вычисляем её предел при λ → 0, где  – это ранг разбиения.
– это ранг разбиения.
4. Если предел интегральной суммы существует, является конечным и не зависит ни от способа разбиения дуги (l) на элементарные части, ни от выбора на них точек 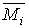 , то он называется криволинейным интегралом I рода от функции
, то он называется криволинейным интегралом I рода от функции
f (x, y, z) по линии l:

|
Свойства определённого интеграла по фигуре
пусть функция f(p)  непрерывна на фигуре Ф т.е. ОИ по фигуре Ф существует, тогда выполняются следующие свойства:
непрерывна на фигуре Ф т.е. ОИ по фигуре Ф существует, тогда выполняются следующие свойства:
1.  f1(p)∓f2pdw=
f1(p)∓f2pdw=  f1pdw∓
f1pdw∓  f2pdw
f2pdw
2.  kf(p)dw=k
kf(p)dw=k  f(p)dw
f(p)dw
3. если фигуру Ф  разбить на конечное число частей, то интеграл равен сумме частей интегралов.
разбить на конечное число частей, то интеграл равен сумме частей интегралов.
4. если 
 dw=w
dw=w  ,
,
то 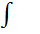 dl=l,
dl=l,  ds=s,d
ds=s,d  σ=σ,
σ=σ, 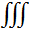 dv=v
dv=v
5. если f1(p)<f2(p), то  f1pdw<
f1pdw<  f2pdw
f2pdw
6. 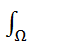 /f(p)dw/≤
/f(p)dw/≤  /f(p)/dw
/f(p)/dw
7. оценка интеграла по фигуре. Если m и M наибольшее и наименьшее значение функции f(p) на фигуре Ф, то mw ≤  f(p)dw≤Mw
f(p)dw≤Mw 
8. (о среднем значении) если функция f(p) непрерывна на Ф с
мерой w, то найдется точка Р ∈Ф, то  f(p)dw=
f(p)dw=  (Po)w
(Po)w
Вычисление криволинейного интеграла 1-ого рода
волинейный интеграл 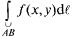 легко сводится к определенному интегралу. Примем за параметр длину дуги
легко сводится к определенному интегралу. Примем за параметр длину дуги 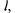 отсчитываемую от точки А по кривой
отсчитываемую от точки А по кривой  получим параметрическое представление кривой
получим параметрическое представление кривой  где
где 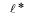 —
—
длина дуги 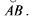 Пусть в (25.3) промежуточным точкам
Пусть в (25.3) промежуточным точкам 
соответствует 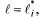 т.е.
т.е. 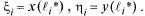 Тогда
Тогда
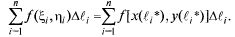
Последняя сумма является интегральной для определения интеграла 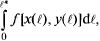 т.е.
т.е.
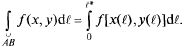 (25.4)
(25.4)
Эта формула доказывает существование криволинейного интеграла 1 рода от функции 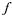 (х,у), непрерывной в D, если
(х,у), непрерывной в D, если 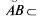 D — непрерывная кусочно-гладкая кривая.
D — непрерывная кусочно-гладкая кривая.
Рассмотрим формулы для вычислений криволинейного интеграла в следующих случаях:
а) 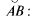 х = x(t), у = y{t),
х = x(t), у = y{t), 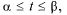 где x{t) и y{t) непрерывно
где x{t) и y{t) непрерывно
дифференцируемы на  тогда (см. разд. 18.3)
тогда (см. разд. 18.3)

т.е. из (25.4) имеем
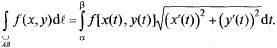
Формула может быть обобщена на пространственный случай, т.е. если 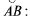 х = x(t), у = y(t), z = z(t),
х = x(t), у = y(t), z = z(t), 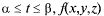 непрерыв-
непрерыв-
на в D, 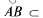 В, тогда
В, тогда
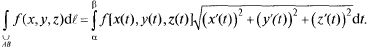
Аналогично записывается формула для большего числа переменных.