Вычисление ДИ в полярных координатах
Пусть область D записывается системой неравенств в полярных координатах:
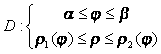
Такая область называется правильной в полярной системе координат, если каждый луч, выходящий из полюса, пересекает границу области не более, чем в 2-x точках.
По определению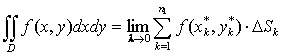 
.
Т. к. значение двойного интеграла не зависит от способа разбиения области D на элементарные части, то сделаем это разбиение координатными линиями полярной системы координат (лучами из полюса и концентрическими окружностями).
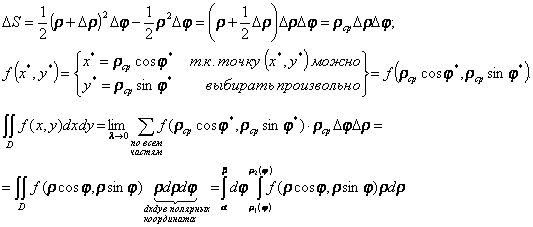
Переведенный в полярные координаты двойной интеграл сведен к повторному по имеющейся записи области D неравенствами для переменных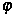 
и 
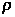. В результате получаем формулу для вычисления двойного интеграла в полярных координатах:
.
Обратите внимание, что в правой части формулы присутствует множитель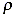 
- это якобиан (определитель Якоби) преобразования, который находится следующим образом:
Вычисление тройного интеграла в декартовых координатах
Пусть в трехмерной области V пространства OXY задана функция 
. Разобьем произвольным образом область V на элементарные подобласти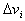 
, в каждой подобласти зафиксируем произвольную точку ( 
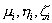) и составим трехмерную интегральную сумму 
.
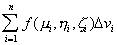Тройным интегралом от функции по ограниченной области V называется предел последовательности соответствующих интегральных сумм при стремлении к нулю наибольшего из диаметров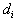 
элементарных областей 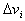, если этот предел не зависит ни от способа разбиения области V на части, ни от выбора точек 
:
.
Вычисление тройного интеграла сводится к вычислению двойного интеграла и одного однократного либо к вычислению трех повторных интегралов. Если область V ограничена сверху поверхностью 
, снизу поверхностью 
, с боков – прямым цилиндром, вырезающим на плоскости OXY область D, то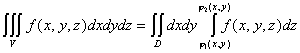 
.
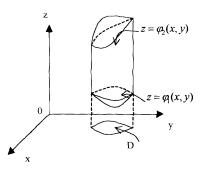
Рис. 9
С помощью тройного интеграла объем тела, изображенного на рис. 9, вычисляют по формуле: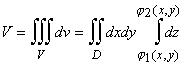 
.
Вычисление Тройного интеграла в цилиндрических координатах
Рассмотрим цилиндрическую систему координат: Оrφz, которая совмещена с декартовой системой координат Оxyz (рис. 2.19).
При этом
Вычислим Якобиан перехода от декартовой системы к цилиндрической:
Следовательно, 
Тогда тройной интеграл примет вид:
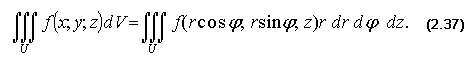
Вычисление тройного интеграла в сферических координатах
Рассмотрим сферическую систему координат ОρΘφ, совмещённую с декартовой системой Оxyz. При этом максимальные пределы изменения сферических координат таковы: 0 ≤ φ ≤ 2 π, 0 ≤ ρ ≤ ∞
Из рис. 2.21 нетрудно вывести следующие формулы, связывающие декартовые и сферические координаты:
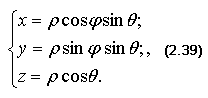
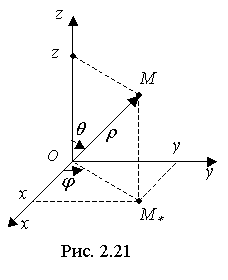
с помощью которых получим Якобиан преобразования:
Таким образом, переход к сферическим координатам в тройном интеграле осуществляется по формулам:
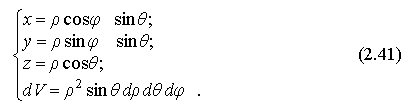
Вычисление ПИ-1
Поверхностный интеграл первого рода от функции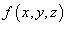 
по поверхности S определяется следующим образом:
где частные производные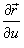 
и 
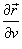равны
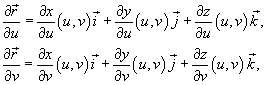
а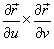 
означает векторное произведение. Вектор 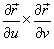перпендикулярен поверхности в точке 
.
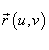Абсолютное значение 
называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).
|