| Номера интервала i | Серединные значения xi | Частоты ni | ni·xi |
| Σ |
Как следует из табл. 4, среднее выборочное значение:
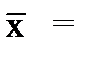
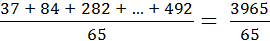= 61см.
Средняя величина обобщает количественное выражение признака, погашает индивидуальные различия статистических величин совокупности, вызванные случайными обстоятельствами.
Кроме среднего выборочного значения существуют другие характеристики, определяющие положение центра эмпирического распределения: медиана и мода.
2. Медиана (Ме) – выборочное значение, разделяющее вариационный ряд на две части, равные по числу вариант.
При нечетном объеме выборки (n = 2k+1) Ме = хk+1,
при чётном (n = 2k) значение медианы равно: 
Приведем расчет медианы для примера 1. Исходные данные результатов прыжков спортсменов ранжируют (располагают в порядке возрастания или убывания): 37, 40, 43, 47, 47, 47, 47, 48, 48, 50, 50, 50, 51, 51, 52, 53, 53, 53, 54, 54, 55, 56, 57, 57, 57, 57, 57, 57, 58, 59, 59, 59, 60, 60, 60, 61, 61, 61, 61, 62, 62, 63, 64, 65, 65, 66, 66, 66, 67, 69, 69, 70, 71, 71, 73, 76, 76, 76, 77, 81, 81, 81, 82, 83, 83.
Объем выборки n = 65 = 2·32 + 1, тогда Ме = х32+1 = x33 = 60 см.
При вычислении медианы в интервальном вариационном ряду сначала находят медианный интервал (т. е. содержащий медиану) по накопленным частотам или частостям. Медианным является первый интервал, накопленная частота которого превышает половину объема совокупности:
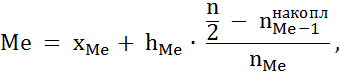
где xMe – нижняя граница медианного интервала;
hMe – ширина медианного интервала;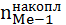 
- накопленная частота интервала, предшествующего медианному;
nMe – частота медианного интервала; n – объём выборки.
|
|
В табл. 2 примера 1 медианным является интервал наблюдений от 59,5 см. до 64,5 см., так как именно его накопленная частота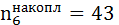 
превышает половину числа проведенных измерений выполнения прыжков вверх с места спортсменов-баскетболистов.
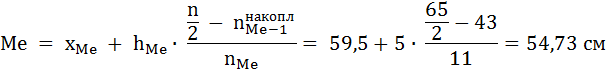
3. Мода выборки (Мо) – варианта, имеющая наибольшую частоту или относительную частоту. Мода представляет высшую точку графического распределения – полигона частот.
Иногда выборка содержит более чем одну моду (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае говорят, что совокупность мультимодальна. Мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.
В интервальных вариационных рядах для нахождения моды сначала по наибольшей частоте определяют модальный интервал (интервал, содержащий моду), затем её рассчитывают по формуле:
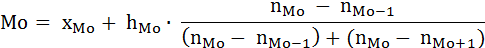
где xMo – нижняя граница модального интервала;
hMo – длина (шаг) модального интервала;
nMo - частота модального интервала;
nMo-1, nMo+1 - частоты, соответственно в предыдущем и следующим за модальным интервалах.
Значение моды данных примера 1 равно 57 см (встречается 6 раз). Модальный интервал 54,5 – 59,5 см (частота n5 =12).
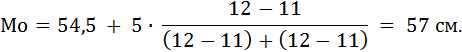
Средние значения не дают полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки.