Вероятности, признанные достаточным для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называют доверительными.
Обычно, в качестве доверительных вероятностей выбирают значения 0,95; 0,99; 0,999 (их принято выражать в процентах – 95%, 99%, 99,9%). Чем выше мера ответственности, тем более высокий уровень доверительной вероятности: 99% или 99,9%.
Доверительная вероятность 0,95 (95%) считается достаточной в научных исследованиях в области физической культуры и спорта.
Интервал, в котором с заданной доверительной вероятностью находится выборочное среднее арифметическое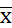 
генеральной совокупности, называется доверительным интервалом.
Уровень значимости оценивания – малое число α, значение которого предполагает вероятность того, что 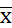выходит за границы доверительного интервала. В соответствии с доверительными вероятностями: α1= (1- 0,95) = 0, 05; α2 = (1 – 0,99) = 0, 01 и т.д.
Доверительный интервал для среднего (математического ожидания) a нормального распределения:
,
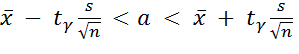где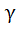 
- надежность (доверительная вероятность) оценивания; 
- выборочное среднее; s - исправленное среднеквадратическое отклонение; n – объем выборки; tγ - величина, определяемая по таблице распределения Стьюдента (см. приложение, табл. 1) при заданных n и γ.
Чтобы найти границы доверительного интервала среднего значения генеральной совокупности необходимо:
1. Вычислить 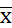и s.
2. Следует задасться доверительной вероятностью (надежностью) γ оценивания 0,95 (95 %) или уровнем значимости α 0,05 (5 %)
3. По таблице t – распределения Стьюдента (приложение, табл. 1) найти граничные значения tγ.
Так как t– распределение симметрично относительно нулевой точки, достаточно знать только положительное значение t. Например, если объем выборки n=16, то число степеней свободы (degrees of freedom, df) t – распределения df = 16 - 1=15. По табл. 1 приложения t 0,05 = 2,13.
|
|
4. Находим границы доверительного интервала для α = 0,05 и n = 16:
Границы доверия: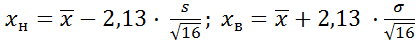 
При больших объемах выборки (n ≥ 30) t – распределение Стьюдента переходит в нормальное. Поэтому доверительный интервал для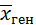 
при n ≥ 30 можно записать следующим образом:
;
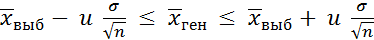где u - процентивные точки нормированного нормального распределения [6 - 8].
Для стандартных доверительных вероятностей (95%, 99%; 99, 9%) и уровней значимости α значения (u) приведены в таблице 8.
Таблица 8
Значения для стандартных доверительных уровней α
| α | u |
| 0,05 | 1,96 |
| 0,01 | 2,58 |
| 0,001 | 3,28 |
Опираясь на данные примера 1, определим границы 95 % - го доверительного интервала ( α = 0,05) для среднего результата прыжка вверх с места. В нашем примере объем выборки n = 65, тогда для определения границ доверительного интервала можно использовать рекомендации для большого объема выборки:
1. Среднее выборочное значение 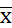= 60,8 см., исправленное среднеквадратическое отклонение s = 11,2 см.
2. Задаемся доверительной вероятностью γ = 0,95 (95%);
3. Из таблицы 8 находим u 0,05 = 1,96;
4. Определяем границы искомого доверительного интервала:
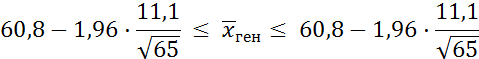
60,8 – 1,96·1,38 ≤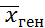 
≤ 60,8 + 1,96·1,38
58,1 см ≤ 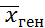≤ 63,5 см
Иными словами данные по высоте прыжка у 65 испытуемых позволяют судить о типичной величине этого теста для всех спортсменов - баскетболистов с некоторой неопределённостью.
Истинное значение среднего результата прыжка вверх с места спортсменов-баскетболистов находится в интервале от 58,1 см. до 63,5 см. с доверительной вероятностью γ = 0, 95 (95%).
|
|