Характеристики рассеивания

Основными характеристиками рассеивания, применяемых для оценки вариации величин относительно выборочной средней, являются дисперсия, среднеквадратическое отклонение, коэффициент вариации.

1. Дисперсия (от лат. dispersio - рассеяние) – среднее арифметическое из квадратов отклонений величин x_i от их среднего арифметического.

Дисперсия (D) - мера рассеивания (отклонения от среднего), определяется следующим образом - из каждого варианта вычитают среднюю арифметическую, разность возводят в квадрат и умножают на соответствующую ей частоту. Далее определяют сумму всех произведений и делят её на объём совокупности:

D =

Для сгруппированных данных дисперсию определяют:

D =

Размерность дисперсии не совпадает с единицами измерения варьирующего признака.

При решении практических задач помимо использования формул расчета выборочной дисперсии используется величина, которая называется исправленной дисперсией. Дело в том, что значение выборочной дисперсии дает заниженные значения по отношению к действительной дисперсии, поэтому при малых выборках (n < 30) необходимо применять исправленную дисперсию и среднеквадратическое отклонение [2, 7]:

или

2. Выборочное и исправленное среднеквадратическое отклонение (σ, s) – корень квадратный из дисперсии. Размерность среднеквадратического отклонения в отличие от размерности дисперсии совпадает с единицами измерения экспериментальных данных, поэтому его в основном используют для характеристики рассеивания изучаемого признака.

Приведем расчет дисперсии (табл. 5) для примера 1.

Промежуточные вычисления расчета дисперсии

№п/п	Серединные значения, xi	Классовые частоты, ni
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
сумма

Дисперсия для сгруппированных данных примера равна:

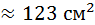
Среднеквадратическое отклонение соответственно равно:

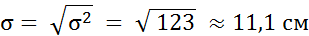
Исправленное среднеквадратическое отклонение равно:

Заметим, что формулы для вычисления выборочной и исправленной дисперсий отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n < 30 [2, 7].

3. Коэффициент вариации (v) – является относительной мерой рассеивания признака, используется как показатель однородности выборочных наблюдений (табл. 6).

Коэффициент вариации - это отношение среднеквадратического отклонения к средней арифметической, выраженное в процентах. Кроме того, коэффициент вариации часто используется при сопоставлении (сравнении) степени варьирования различных признаков, выраженных в различных единицах измерения.

Для определения характера рассеивания безразмерный коэффициент вариации v рассчитывают по формуле:

,

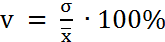где σ – среднеквадратическое отклонение;

- среднее арифметическое выборочных данных.

Таблица 6