С помощью вышеприведенных методов можно находить первоначальный план поставок. Теперь надо выяснить, является ли найденный план оптимальным и, если нет, то, как его оптимизировать. Для этого надо составить матрицу оценок.
Оценка клетки (i, j) вычисляется по следующему правилу: оценка i-й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j). Оценки строки и столбца выбираются таким образом, чтобы оценки всех отмеченных клеток были равны нулю. После этого оценки всех клеток записываются в виде матрицы – матрицы оценок. Если матрица оценок не содержит отрицательных чисел, то получен оптимальный план поставок. Иначе проводится оптимизация плана поставок.
Двигаясь из клетки с отрицательно оценкой по отмеченным клеткам (причем запрещается делать два последовательных шага в одной строке или в одном столбце), строят так называемый цикл пересчета. Внутри этого цикла перераспределяются поставки. Для полученной таблицы находят матрицу оценок и т.д. Рассмотрим подробнее эту схему на конкретном примере.
Пример 3. В примере 1 был получен план поставок. Исследуем его на оптимальность.
Таблица 2.16 – Исходные данные для исследования плана поставок на оптимальность
 60
| 130
| 120
| |||||
| | |||||||
| 240
| 2
|
Начинать можно с любой строки или столбца. Начнем с 1-го столбца, приписав ему ноль (впрочем, на 1-м шаге можно приписать столбцу любую оценку). В 1-м столбце находятся две отмеченные клетки (1,1) и (2,1). Их оценки должны быть нулевыми. Из этого условия, зная оценку 1-го столбца, найдем оценки 1-й и 2-й строк.
Оценка клетки (1,1) = оценка 1-й строки + оценка 1-го столбца + число в левом верхнем углу клетки (1,1) = оценка 1-й строки 
(так должно быть для отмеченной клетки). Отсюда оценка 1-й строки 
.
Оценка клетки (2,1) = оценка 2-й строки + оценка 1- го столбца + число в левом верхнем углу клетки (2,1) = оценка 2-й строки 
(так должно быть для отмеченной клетки). Отсюда оценка 2-й строки 
. Найденные оценки столбцов запишем под таблицей, найденные оценки строк – справа от таблицы.
После этого получаем таблицу 2.17.
Таблица 2.17 - Оценки строк и столбцов
| 60
| 130
| 120
| ||||||
| −5 | ||||||||
| | −4 | |||||||
| 240
| 2
| |||||||
Теперь надо найти отмеченную клетку, для которой известны оценка строки или оценка столбца. Например, это клетка (2,2). Для нее известна оценка строки. Оценка клетки (2,2) = оценка 2-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (2,2) = (−4) + оценка 2-го столбца 
. Отсюда оценка 2-го столбца 
После этого шага получаем таблицу 2.18.
Таблица 2.18 - Измененные оценки. Шаг 1.
| 60
| 130
| 120
| ||||||
| −5 | ||||||||
| | −4 | |||||||
| 240
| 2
| |||||||
Для отмеченной клетки (2,3) мы знаем только оценку строки. Оценка клетки (2,3) = оценка 2-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (2,3) = (−4) + оценка 3-го столбца 
. Отсюда оценка 3-го столбца = 1.
После этого шага получаем таблицу 2.19.
Таблица 2.19 – Измененные оценки. Шаг 2.
| 60
| 130
| 120
| ||||||
| −5 | ||||||||
| | −4 | |||||||
| 240
| 2
| |||||||
Оценка клетки (3,3) = оценка 3-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (3,3) = оценка 3-й строки 
. Отсюда оценка 3-й строки 
После этого шага получаем таблицу 2.20.
Таблица 2.20 – Измененные оценки. Шаг 3.
| 60
| 130
| 120
| ||||||
| −5 | ||||||||
| | −4 | |||||||
| 240
| 2
| −5 | ||||||
Оценка клетки (3,4) = оценка 3-й строки + оценка 4-го столбца + число в левом верхнем углу клетки (3,4 
оценка 4-го столбца 
Отсюда оценка 4-го столбца 
.
После этого шага получаем таблицу 2.21.
Таблица 2.21 – Оценки для всех строк и столбцов
| 60
| 130
| 120
| ||||||
| −5 | ||||||||
| | −4 | |||||||
| 240
| 2
| −5 | ||||||
| −2 |
Найдены оценки всех строк и столбцов. Вычислим оценки всех клеток и составим матрицу оценок.
Оценка клетки (1,2) = оценка 1-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (1,2) 
.
Оценка клетки (1,3) = оценка 1-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (1,3) 
И т.д.
Получаем следующую матрицу оценок: 
.
Так как матрица оценок содержит отрицательные числа, то наш план поставок является неоптимальным. Проведем его оптимизацию. Выбираем клетку с наименьшей оценкой. Это клетка (1,4). Ее оценка равна −5. Задача – построить цикл пересчета. Выходя из клетки (1,4) и двигаясь только по отмеченным клеткам, нужно вернуться в стартовую клетку (1,4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце. Например, подходит цикл (1,4) – (1,1) – (2,1) – (2,3) – (3,3) – (3,4) – (1,4). Нарисуем этот цикл (рисунок 2.1.). Для каждой клетки указаны ее индексы и объем поставок.
Стартовой клетке (1,4) припишем знак «+». Двигаясь по циклу, чередуем знаки. Среди поставок в клетки со знаком «−» (это клетки (1,1), (2,3), (3.4)) найдем минимальную: 
. После этого в клетках со знаком «−» уменьшим поставки на этот минимум, а в клетках со знаком «+» увеличим этот минимум. Клетка (1,4) становится отмеченной.
| (1,1) |
| (1,4) |
| (2,1) |
| (2,3) |
| (3,3) |
| (3,4) |
| + |
| + |
| + |
Рисунок 2.1 – Цикл пересчета
Если получена одна клетка с нулевой поставкой, то она становится пустой. Если таких две, то только одну из них с наибольшим тарифом объявляем пустой. А в другую делаем нулевую поставку. Это делается для выполнения соотношения: число отмеченных клеток = число строк + число столбцов – 1. Получаем новый план поставок (таблица 2.22).
Нужно следить, чтобы суммы поставок по строкам и столбцам были равны мощностям поставщиков и спросу потребителей соответственно.
Таблица 2.22 – Новый план поставок
| 60
| 130
| 120
| |||||
| | −4 | |||||||
| 240
| 2
| −5 | ||||||
| −2 |
Для нового плана находим оценки строк и столбцов. Затем получим матрицу оценок клеток: 
.
План является неоптимальным, так как оценки клеток (2,4) и (3,1) меньше нуля. Строим для нее цикл пересчета: (3,1) – (2,1) – (2,3) – (3,3) – (3.1) (рисунок 2.2.).
| (2,3) |
| (3,1) |
| (3,3) |
| + |
| + |
| − |
| − |
| (2,1) |
Рисунок 2.2 – Цикл пересчета для новой матрицы
. Клетка (2,1) становится пустой, а клетка (3,1) – отмеченной. Новый план поставок – таблица 2.23.
Таблица 2.23 – План поставок после пересчета. Шаг 2.
| 20
| 5
| 3
| ||||||
| 200
| 4
| 5
| −1 | |||||
| −2 | ||||||||
| −2 | −5 |
Для нового плана находим оценки строк и столбцов. Затем получим матрицу оценок клеток: 
.
| (2,4) |
| (2,3) |
| (3,3) |
| (3,4) |
| + |
| + |
| − |
| − |
Рисунок 2.3 – Цикл пересчета, вариант 3
. Клетка (2,1) становится пустой. Новый план поставок – таблица 2.24.
Таблица 2.24 – План поставок после пересчета. Шаг 3
| 20
| 5
| 3
| 8
| |||||
| 2
| -2 | |||||||
| -1 | -2 | -5 |
Находим оценки строк и столбцов. Получаем матрицу оценок:
Матрица оценок не содержит отрицательных чисел. Получен оптимальный план поставок. Суммарные затраты на перевозку груза равны: 
. Суммарные затраты на перевозку груза для первоначального плана были 1610.
Поставщик А1 должен поставить 20 единиц груза потребителю В4, поставщик А2 должен поставить 130 единиц груза потребителю В2 и 70 единиц груза потребителю В4. Поставщик А3 должен поставить 60 единиц груза потребителю В1, 120 единиц груза потребителю В3 и 60 единиц груза потребителю В4.
Открытая модель
Открытая модель сводится к закрытой модели с использованием фиктивного поставщика или фиктивного потребителя.
Фиктивный потребитель
Если суммарная мощность поставщиков больше суммарного спроса потребителей, то вводится фиктивный потребитель, которому приписывается спрос, равный разнице между суммарной мощностью поставщиков и суммарным спросом потребителей. Стоимость перевозки единицы груза от поставщиков до фиктивного потребителя полагается равной нулю. Полученная закрытая модель решается. Груз, предназначенный фиктивному потребителю, остается у поставщика.
Пример 4.
Исходные данные приведены в таблице 2.25.
Таблица 2.25 – Исходные данные для примера 4.
Суммарная мощность поставщиков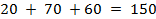 
, суммарный спрос потребителей 
Это открытая модель. Вводим фиктивного потребителя, которому припишем спрос 
. Стоимость перевозки единицы груза до фиктивного потребителя равна нулю. Получаем следующую закрытую модель (таблица 2.26).
Таблица 2.26 – Исходные данные с фиктивным потребителем
Фиктивный поставщик
Если суммарная мощность поставщиков меньше суммарного спроса потребителей, то вводится фиктивный поставщик, которому приписывается мощность, равная разнице между суммарным спросом потребителей и суммарной мощностью поставщиков. Стоимость перевозки единицы груза от фиктивного поставщика до потребителей полагается равной нулю. Полученная закрытая модель решается. Потребитель, приписанный к фиктивному поставщику просто не получает соответствующего груза.
Пример 5.
Исходные данные приведены в таблице 2.27.
Таблица 2.27 - Исходные данные для примера 5
Суммарная мощность поставщиков 
, суммарный спрос потребителей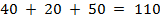 
. Модель – открытая. Вводим фиктивного поставщика, которому припишем мощность 
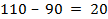. Стоимость перевозки единицы груза от фиктивного поставщика до потребителей равна нулю. Получаем следующую закрытую модель (таблица 2.28).
Таблица 2.28 - Исходные данные с фиктивным поставщиком