Одной из основных задач транспортной логистики является задача выбора рационального маршрута перевозки груза. При определении маршрута доставки груза основными критериям являются следующие:
· суммарная величина расходов на транспортировку;
· срок доставки груза;
· гарантированность сроков доставки;
· надежность и безопасность транспортировки товара;
· сезонность и зависимость от погодных условий.
Выбор оптимального маршрута доставки производится, как правило, экспедитором грузовладельца при получении заявки на организацию транспортировки нового для него груза или известного груза на новом направлении. На основании предварительной оценки возможных решений определяются 2–4 конкурентоспособных варианта. По каждому из них собираются исходные данные, а затем на основе выполненных расчетов рекомендуется оптимальный вариант. На практике наиболее часто используются критерии стоимости перевозки и срока доставки.
Задача: Определить рациональный маршрут перевозки 20 футового контейнера из порта Пуссан (Республика Корея) до терминала в Москве (Российская Федерация). На рисунке 4.1 приведены возможные маршруты доставки, а в таблице 4.1 - их стоимостные и временные характеристики, полученные по результатам исследования деятельности крупных экспедиторских компаний.
Решение. Из рисунка 4.1 видно, что маршрут №1 следующий: из Пуссана груз следует морем до порта Гамбург, затем перегружается в другое судно и следует до порта Котка. Из порта Котка следует автомобильным транспортом до Москвы и доставляется на склад грузополучателя.
Маршрут№2: из Пуссана груз следует морем до порта Гамбург, затем перегружается в другое судно и следует до Санкт-Петербурга. Из Санкт-Петербурга следует до Москвы и доставляется на склад автомобильным транспортом.
|
|
Маршрут №3: из Пуссана груз следует морем до порта Гамбург, затем перегружается в другое судно и следует до Санкт-Петербурга. Из Санкт-Петербурга следует до Москвы и доставляется на склад железнодорожным транспортом.
Маршрут№4: из Пуссана груз следует морем до порта Гамбург, затем перегружается в другое судно и следует до Санкт-Петербурга. Из Санкт-Петербурга доставляется на склад грузополучателя.
| В |
| Терминал |
| К |
| Г |
| П |
| Получатель |
| СП |
Рисунок 4.1- Маршруты по направлению Пуссан – Москва
Маршрут№5: из Пуссана груз следует морем до порта Восточный, затем до Москвы и доставляется на склад железнодорожным транспортом.
Таблица 4.1 - Краткая характеристика маршрутов доставки
| Номер маршрута | Характеристика | Виды транспорта |
| Через порт Котка (Финляндия) | Морской + автомобильный | |
| Через порт Санкт-Петербург | Морской + автомобильный | |
| Продолжение таблицы 4.1. | ||
| Через порт Котка | Морской + железнодорожный + автомобильный | |
| Через порт Санкт-Петербург | Морской+железнодорож-ный + автомобильный | |
| Через порт Восточный (по Транссибу) | Морской+железнодорож-ный + автомобильный |
В таблице 4.2 приведены составляющие затрат интермодальной перевозки и общие затраты по вариантам.
Таблица 4.2 - Составляющие затрат перевозки груза
| Номер марш рута | Виды транспорта | Составляющие затрат | Общие затраты, евро | ||
| морская | автомобильная | Железнодо-рожная | |||
| Морской + автомобильный | - | ||||
| Морской + автомобильный | - | ||||
| Морской + железно-дорожный + автомобильный | |||||
| Морской + железно-дорожный + автомобильный | |||||
| Морской + железно-дорожнный + автомобильный |
В таблице 4.3 приведены обобщенные данные о сроках доставки по маршрутам.
|
|
Таблица 4.3 - Сроки доставки груза по вариантам
| Номер маршрута | Морская перевозка | Наземная перевозка | Дополнительное время | Срок доставки |
| 26+3=29 | 2+2=4 | |||
| 26+4=30 | 2+7+1+1=11 | |||
| 26+3=29 | 2+3+2=7 | |||
| 26+4=30 | 2+7+2=11 | |||
Приведенные стоимостные и временные оценки маршрутов представляют собой два критерия, т.е. получена многокритериальная задача. Для получения однокритериальной оценки воспользуемся следующей формулой:
С* = (СТ + Спер) (1 + i) n, (4.1)
где С* – оценка стоимости груза и его доставки с учетом фактора времени (интегральная оценка);
СТ – закупочная стоимость товара;
Спер – стоимость перевозки;
(1 + i) n – множитель наращения процентов по процентной ставке i за n периодов.
Средняя банковская ставка i по краткосрочным валютным кредитам, равна 15% в год.
Величина n может быть рассчитана с учетом срока доставки Т:
n = Т/365, (4.2)
В качестве стоимости перевозки при расчете по формуле используются ставки на соответствующих маршрутах.
Примем для сравнительных расчетов для 20-футового контейнера
СТ = 35 тыс. евро
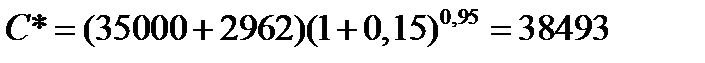-для первого варианта.
-для второго варианта.
|
|
-для третьего варианта.
-для четвертого варианта.
-для пятого варианта.
Результаты расчета интегральной оценки приведены в таблице 4.4.
Таблица 4.4 - Результаты расчета интегральной оценки
| Номер маршрута | Общие затраты | Срок доставки | Интегральная оценка |
Вывод: Пятый маршрут является лучшим, т.к. общие затраты и срок доставки в этом варианте меньше, чем в остальных вариантах.
Исходные данные для самостоятельной работы приведены в Приложении 4.
ПРИМЕНЕНИЕ СЕТЕВЫХ ГРАФИКОВ ДЛЯ ПЛАНИРОВАНИЯ МЕЖДУНАРОДНЫХ ИНТЕРМОДАЛЬНЫХ ПЕРЕВОЗОК ГРУЗОВ
Для построения сетевого графика необходимо определить временные и стоимостные характеристики различных вариантов доставки, каждый из которых характеризуется определенным набором операций и услуг, оказываемых при перевозке. При этом следует учитывать, что при выборе варианта доставки можно использовать не только такие критерии как время и стоимость, но и, например приведенная стоимость.
Пример. В качестве основы возьмем перевозку груза из Хельсинки до терминала в Москве (Российская Федерация) (рисунок 5.1).
Рисунок. 5.1 - Маршруты по направлению Хельсинки – Москва
Решение. Анализируя маршруты доставки, с учетом дополнительных не движенческих (нетранспортных) составляющих, можно построить сетевой график, представляющий собой альтернативные пути доставки (рисунок 5.2). Для первой работы параметры время Т, стоимость С и приведенная стоимость С приравниваются к нулевым значениям. Учитывая, что количество вариантов схем доставки определяет количество значений параметров, в рассматриваемом примере их будет двенадцать.
Охарактеризуем работы, включаемые в сетевой график, а так же параметры времени и стоимости для каждой из них (таблица 5.1).
Стоимость (интегральная оценка) определяется по формуле 4.1. 
Рисунок 5.2 - Варианты доставки контейнера из Хельсинки грузополучателю в Москве.
Таблица 5.1 - Работы по доставке грузов по направлению Хельсинки – Москва
| № работы | Характеристика работы | Стоимость, долл. | Время, дни | |
| Затамаживание груза в Хельсинки | 1,0 | |||
| Оформление документов и погрузка на автомобильный транспорт | 1,0 | |||
| Оформление документов и погрузка на железную дорогу | 3,0 | |||
| Оформление документов и погрузка на судно в п. Хельсинки | 2,0 | |||
| Доставки морским транспортом до п. Санкт-Петербург | 2,0 | |||
| Разгрузка в.п Санкт-Петербург | 1,0 | |||
| Выпуск контейнера из п. Санкт-Петербург собственными силами с таможенной гарантией* | 3,0 | |||
| Выпуск контейнера из п. Санкт-Петербург экспедитором | 1,0 | |||
| Выпуск контейнера из п. Санкт-Петербург под гарантию таможенного перевозчика | - | 2,0 | ||
| Выпуск груза из п. Санкт-Петербург на железную дорогу | 4,0 | |||
| Доставка автомобильным транспортом до Москвы (СВХ) | 1,5 | |||
| Доставка таможенным перевозчиком автомобильного транспорта до Москвы (СВХ) | 1,5 | |||
| Доставка железной дорогой из. П. Санкт-Петербург в Москву (СВХ) | 4,0 | |||
| Доставка автомобильным транспортом из Хельсинки до Москвы (СВХ) | 1 500 | 4,0 | ||
| Доставка железной дорогой из Хельсинки до Москвы (СВХ) | 7,0 | |||
| Растамаживание в Москве собственными силами | 4,0 | |||
| Растамаживание в Москве таможенным брокером | 1,5 | |||
| Доставка по Москве автомобильным транспортом от СВХ до терминала грузополучателя | 0,5 | |||
| * - для выпуска контейнера собственными силами грузовладелец должен быть владельцем склада временного хранения (СВХ) и иметь возможность оформлять гарантийный сертификат |
Таблица 5.2 - Результаты расчета параметров для различных схем доставки
| Номер маршрута (№ п/п) | Схема доставки | Время Т, дни | Стоимость С, у.е. | Интегральная оценка С*, у.е. |
| 1 (1) | 1, 2, 3, 12, 13, 15 | 10,5 | 37 229,38 | |
| 1 (2) | 1, 2, 3, 12, 14, 15 | 8,0 | 37 344,22 | |
| 2 (3) | 1, 2, 4, 12, 13, 15 | 15,5 | 36 303,83 | |
| 2 (4) | 1, 2, 4, 12, 14, 15 | 13,0 | 36 419,84 | |
| 3 (5) | 1, 2, 5, 6, 7, 8, 12, 13, 15 | 15,0 | 37 253,36 | |
| 3 (6) | 1, 2, 5, 6, 7, 8, 12, 14, 15 | 12,5 | 37 368,43 | |
| 3 (7) | 1, 2, 5, 6, 7, 9, 12, 13, 15 | 13,0 | 37 476,09 | |
| 3 (8) | 1, 2, 5, 6, 7, 9, 12, 14, 15 | 10,5 | 37 590,83 | |
| 3 (9) | 1, 2, 5, 6, 7, 10, 12, 13, 15 | 14,0 | 37 389,90 | |
| 3 (10) | 1, 2, 5, 6, 7, 10, 12, 14, 15 | 11,5 | 37 504,79 | |
| 4 (11) | 1, 2, 5, 6, 7, 11, 12, 13, 15 | 18,5 | 37 040,46 | |
| 4 (12) | 1, 2, 5, 6, 7, 11, 12, 14, 15 | 16,0 | 37 155,94 |
В том случае, если маршрут по каким-либо причинам не удовлетворяет грузовладельца, существует два варианта.
Во-первых, выбор может быть произведен на основе одного определяющего на данный момент времени показателя. Например, если определяющим является стоимость доставки, то предпочтительным будет десятый вариант доставки по третьему маршруту. Во-вторых, если важность показателей имеет примерно одинаковое значение и если ни для одной из схем доставки не оказалось, что все значения ниже, чем для любой другой (тогда выбор очевиден), то для выбора схемы перевозки можно использовать критерии принятия решения в условиях неопределенности.
Наиболее известны критерии Лапласа, Вальда, Сэвиджа и Гурвица, позволяющие принимать решение на основе анализа матрицы возможных результатов, которая в нашем случае приведена в таблице 5.2: строки соответствуют возможным действиям Rj (вариантам доставки грузов); столбцы – возможным состояниям “природы” Si (параметрам доставки); элементы матрицы – результат при выборе j -го действия и реализации i -го состояния Vji.
Для получения сопоставимых результатов из анализа исключили пятый маршрут и привели матрицу в относительный вид, поделив элементы каждого столбца на его минимальное значение (таблица 5.3).
Критерий Лапласа опирается на принцип недостаточного основания, согласно которому все состояния природы Si (i = 
) полагаются равновероятными. Таким образом, каждому состоянию Si соответствует вероятность qi:
, (5.1)
Таблица 5.3 - Относительные значения параметров по маршруту Хельсинки – Москва
| Номер маршрута (№ п/п) | Схема доставки | Относительные значения параметров | ||
| Т | С | С * | ||
| 1 (1) | 1, 2, 3, 12, 13, 15 | 1,3125 | 1,9100 | 1,0255 |
| 1 (2) | 1, 2, 3, 12, 14, 15 | 1,0000 | 2,0478 | 1,0287 |
| 2 (3) | 1, 2, 4, 12, 13, 15 | 1,9375 | 1,0000 | 1,0000 |
| 2 (4) | 1, 2, 4, 12, 14, 15 | 1,6250 | 1,1377 | 1,0032 |
| 3 (5) | 1, 2, 5, 6, 7, 8, 12, 13, 15 | 1,8750 | 1,8733 | 1,0262 |
| 3 (6) | 1, 2, 5, 6, 7, 8, 12, 14, 15 | 1,5625 | 2,0110 | 1,0293 |
| 3 (7) | 1, 2, 5, 6, 7, 9, 12, 13, 15 | 1,6250 | 2,1028 | 1,0323 |
| 3 (8) | 1, 2, 5, 6, 7, 9, 12, 14, 15 | 1,3125 | 2,2406 | 1,0355 |
| 3 (9) | 1, 2, 5, 6, 7, 10, 12, 13, 15 | 1,7500 | 2,0110 | 1,0299 |
| 3 (10) | 1, 2, 5, 6, 7, 10, 12, 14, 15 | 1,4375 | 2,1488 | 1,0331 |
| 4 (11) | 1, 2, 5, 6, 7, 11, 12, 13, 15 | 2,3125 | 1,6336 | 1,0203 |
| 4 (12) | 1, 2, 5, 6, 7, 11, 12, 14, 15 | 2,0000 | 1,7713 | 1,0235 |
| Строки - возможные действия Rj (варианты доставки грузов); столбцы – возможные состояния «природы» Si (критерии доставки); элементы матрицы – результат при выборе j -го действия и реализации i -го состояния Vj i |
Для принятия решения для каждого действия Rj вычисляется среднее арифметическое значение потерь:
, (5.2)
Среди Mj (R) выбирают минимальное значение, если, как в рассматриваемом случае, матрица возможных результатов представлена матрицей потерь (или максимальное, во всех других ситуациях), которое и будет соответствовать оптимальной стратегии:
, (5.3)
где W – значение параметра, соответствующее оптимальной стратегии (варианту доставки груза).
Вероятность qi = 1/3. Для первого маршрута доставки найдем среднее арифметическое значение потерь М 1 = 1/3 * (1,3125 + 1,9100 + 1,0255) = 1,4160.
Критерий Вальда (минимаксный или максиминный критерий), основанный на принципе наибольшей осторожности. В случае, когда результат Vji представляет собой потери, при выборе оптимальной стратегии используется минимаксный критерий. Требуется на первом этапе в каждой строке найти наибольший элемент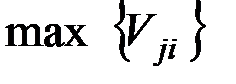 
, а далее выбирается действие Rj (строка j), которому будет соответствовать наименьший элемент из этих наибольших элементов:
, (5.4)
Таким образом, для первого маршрута наибольшее значение 1,9100, для второго - 2,0478.
Критерий Сэвиджа использует матрицу рисков, элементы rji которой определяют по формуле:
, (5.5)
Таким образом, rji есть разность между наилучшим значением в столбце i и значениями Vji при том же i. Согласно критерию рекомендуется выбрать ту стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации:
, (5.6)
Для первого варианта доставки: r 11 = 1,3125 – 1,00 = 0,3125; r 12 = 1,9100 – 1,00 = 0,9100; r 13 = 1,0255 – 1,00 = 0,0255. Максимальное значение – 0,9100.
Критерий Гурвица основан на двух следующих предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью (1 - 
) и в самом выгодном состоянии с вероятностью 
, где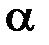 
- коэффициент доверия. Если элементы матрицы представляют собой потери, то выбирают действие, которое выполняет следующее условие:
, (5.7)
Значение 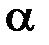определяется в зависимости от склонности лица, принимающего решение, к пессимизму или к оптимизму. При отсутствии ярко выраженной склонности наиболее часто используется 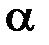= 0,5.
Для первого варианта 0,5 * 1,0255 + 0,5 * 1,9100 = 1,4559.
Сводные данные по маршрутам со значениями перечисленных критериев приведены в таблице 5.4.
Таблица 5.4 - Выбор схемы доставки по критериям принятия решения
| Номер маршрута (N п/п, j) | Критерий Лапласа Mj (R) | Критерий Вальда max (Vji) | Критерий Севиджа max (rji) | Критерий Гурвица 
|
| 1 (1) | 1,4160 | 1,9100 | 0,9100 | 1,4678 |
| 1 (2) | 1,3588 | 2,0478 | 1,0478 | 1,5239 |
Продолжение таблицы 5.4.
| 2 (3) | 1,3125 | 1,9375 | 0,9375 | 1,4688 |
| 2 (4) | 1,2553 | 1,6250 | 0,6250 | 1,3141 |
| 3 (5) | 1,5915 | 1,8750 | 0,8750 | 1,4506 |
| 3 (6) | 1,5343 | 2,0110 | 1,0110 | 1,5202 |
| 3 (7) | 1,5867 | 2,1028 | 1,1028 | 1,5676 |
| 3 (8) | 1,5295 | 2,2406 | 1,2406 | 1,6380 |
| 3 (9) | 1,5970 | 2,0110 | 1,0110 | 1,5205 |
| 3 (10) | 1,5398 | 2,1488 | 1,1488 | 1,5909 |
| 4 (11) | 1,6555 | 2,3125 | 1,3125 | 1,6664 |
| 4 (12) | 1,5983 | 2,0000 | 1,0000 | 1,5117 |
Вывод: 4 вариант по 2 маршруту перевозки является лучшим, т.к. имеет наименьшие значения критериев принятия решений, чем в остальных вариантах.
Исходные данные для самостоятельной работы приведены в Приложении 4.