В Excel существует надстройка «Поиск решения (Solver)», которая, в частности, помогает решать транспортные задачи. Нужно воспользоваться меню Сервис – Поиск решения. Если в меню Сервис отсутствует команда Поиск решения, необходимо выполнить команду Сервис – Надстройки. Найти элемент Поиск решения и поставить «галочку» рядом с ним. Если в окне Надстройки нет элемента Поиск решения, то необходимо доустановить Excel.
Пример 6.
Рассматривается транспортная задача с исходными данными, приведенными в таблице 2.29.
Таблица 2.29 - Исходные данные для примера 6
В 1-м столбце указаны мощности поставщиков, в 1-й строке – спрос потребителей. Остальные числа таблицы – это стоимость перевозки единицы груза от соответствующего поставщика к соответствующему потребителю. Например, стоимость перевозки единицы груза от 3-го поставщика ко 2-му потребителю равна 4. Нужно составить оптимальный план поставок.
Если модель открытая, то ее нужно свести к закрытой модели. При решении закрытой модели можно воспользоваться Excel. В данном случае модель закрытая 
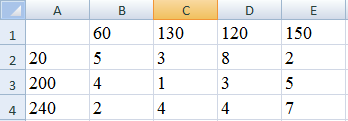
Рисунок 2.4 – Исходные данные
Вводим формулы. Выделяем ячейку В8, в которой вычисляется целевая функция (используется функция суммпроизв (см. рисунок 2.5.)). Вызываем Сервис – Поиск решения. В диалоговом окне в поле ввода «Установить целевую ячейку» уже содержится $B$8. Установим переключатель Равный минимальному значению. В поле ввода, и зменяя ячейки нужно указать $B$5:$E$7.
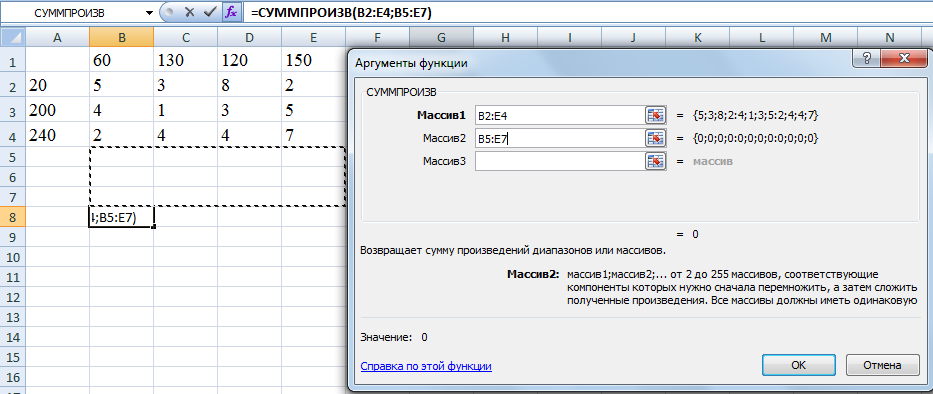
Рисунок 2.5 – Целевая функция
Щелкнем кнопку «Добавить». Появится диалоговое окно «Добавление ограничения». В поле ввода Ссылка на ячейку укажем $B$10. Правее в выпадающем списке с условными операторами выберем =. В поле ввода Ограничение введем $A$10. Щелкнем кнопку «Добавить» и ведем другие ограничения (В1=В5+6+В7, А2=В5+С5+D5+E5 и т.д.). ОК. Мы окажемся в диалоговом окне и увидим введенные ограничения. С помощью кнопок «Изменить» и «Удалить» мы можем изменить и удалить ограничение (см. рисунок 2.6.).
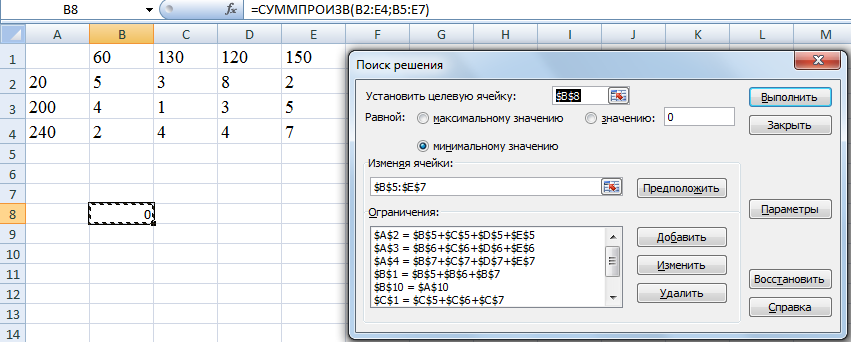
Рисунок 2.6 – Поиск решения
Щелкнем кнопку «Параметры». Установим два флажка: Линейная модель и Неотрицательные значения. ОК. Выполнить.
В ячейке B8 указано 1540 (см. рисунок 2.7.). Это минимальные затраты на перевозку. В ячейках В5:Е7 указаны значения оптимального плана поставок.
Рисунок 2.7 – Оптимальный план поставок
Из рисунка 2.7. видно, что 1-й поставщик должен доставить 20 единиц груза 4-му потребителю, 2-й поставщик должен доставить 130 единиц груза 2-му потребителю и 70 единиц груза 4-му потребителю. 3-й поставщик должен доставить 60 единиц груза 1-му потребителю, 120 единиц груза 3-му потребителю и 60 единиц груза 4-му потребителю.
Транспортная сеть
Транспортная задача может быть задана в виде специальной схемы – транспортной сети. Пункты расположения поставщиков и потребителей изображаются кругами и называются вершинами сети. Мощности поставщиков будем отмечать положительными числами, а спрос потребителей – отрицательными числами. Дороги, связывающие поставщиков и потребителей, изображаются в виде линий и называются ребрами сети. Реальный масштаб не соблюдается. Возможны вершины с нулевым запасом груза – нулевые вершины.
В процессе решения открытая модель всегда сводится к закрытой модели. Поэтому сначала рассмотрим закрытую модель. Нужно построить первоначальный план поставок любым способом. Поставки груза из вершины в вершину будем обозначать стрелками с указанием величин поставок.
На план поставок налагаются следующие условия:
1) все мощности поставщиков должны быть распределены;
2) весь спрос потребителей должен быть удовлетворен;
3) к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;
4) число стрелок = число вершин – 1;
5) стрелки не должны образовывать замкнутый контур (при этом неважно, двигаемся мы по стрелкам или против них).
Особый случай транспортной задачи в сетевой постановке проявляется в том, что при полном использовании мощностей поставщиков и полном удовлетворении спроса потребителей число стрелок 
, где 
– общее число вершин (в том числе и нулевые). Тогда дополнительно вводится нужное количество стрелок. При этом стрелки не должны образовывать контур.
2.8.1 Первоначальный план поставок в транспортной сети
| −60 |
| −140 |
| −130 |
| −150 |
Рисунок 2.8 – Первоначальный план поставок.
Способ расстановки стрелок может быть любым. Важно только выполнение условий 1 – 5. Все поставки указаны стрелками (см. рисунок 2.9.).
| −60 |
| −140 |
| −130 |
| −150 |
Рисунок 2.9 – План поставок, вариант 2
У нас стрелок пять и вершин семь. Не выполняется следующее условие: число стрелок = число вершин – 1, так как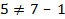 
. Введем еще одну стрелку с нулевой поставкой. Например, 1→5. Получим следующий первоначальный план поставок (см. рисунок 2.10.).
| −60 |
| −140 |
| −130 |
| −150 |
Рисунок 2.10 - План поставок, вариант 3
Затраты на перевозку равны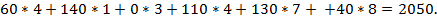 
2.8.2 Проверка плана поставок на оптимальность
Нужно проверить план поставок на оптимальность. Для этого требуется вычислить потенциалы вершин.
Одной из вершин припишем неотрицательное значение потенциала (например, 0). Для наглядности потенциал будем заключать в квадрат. Двигаясь по стрелкам, определяем потенциалы остальных вершин по следующему правилу:
1) если мы двигаемся по стрелке, то к потенциалу вершины прибавляем стоимость перевозки единицы груза по этой стрелке (а не число, которое написано на стрелке);
2) если мы двигаемся против стрелки, то из потенциала вершины вычитаем стоимость перевозки единицы груза по этой стрелке.
После вычисления потенциалов вершин нужно найти характеристики ребер без стрелок по следующему правилу: стоимость перевозки единицы груза для данного ребра – больший потенциал вершин этого ребра + меньший потенциал вершин этого ребра.
Если нет ребер с отрицательными характеристиками, то получен оптимальный план поставок.
Пример 8. Проверим план поставок из примера 7 на оптимальность. Припишем вершине 1 потенциал 0.
Из вершины 1 в вершину 2 ведет стрелка. Стоимость перевозки единицы груза для данного ребра равна 1. Поэтому потенциал вершины 2 равен 0 (потенциал вершины 1) + 1 (стоимость перевозки единицы груза по ребру 1→2) = 1.
Из вершины 1 в вершину 5 ведет стрелка. Стоимость перевозки единицы груза для данного ребра равна 3. Поэтому потенциал вершины 5 равен 0 (потенциал вершины 1) + 3 (стоимость перевозки единицы груза по ребру 1→5) =3.
В вершину 5 из вершины 7 ведет стрелка. Стоимость перевозки единицы груза для данного ребра равна 4. Поэтому потенциал вершины 7 равен 3 (потенциал вершины 5) – 4 (стоимость перевозки единицы груза по ребру 7→5) = −1. И т.д. (см. рисунок 2.11.).
| −60 |
| −140 |
| −130 |
| −150 |
| -5 |
| -1 |
Рисунок 2.11 – План поставок, вариант 4
У нас четыре ребра без стрелок (1,6), (2,4), (3,4), (4,6). Найдем их характеристики.
Характеристика ребра (1,6) = стоимость перевозки единицы груза для ребра (1,6) – больший потенциал вершин ребра (1,6) + меньший потенциал ребра (1,6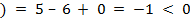 
.
Характеристика ребра (2,4) = стоимость перевозки единицы груза для ребра (2,4) – больший потенциал вершин ребра (2,4) + меньший потенциал ребра (2,4)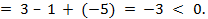 
Характеристика ребра (3,4) = стоимость перевозки единицы груза для ребра (3,4) – больший потенциал вершин ребра (3,4) + меньший потенциал ребра (3,4) 
Характеристика ребра (4,6) = стоимость перевозки единицы груза для ребра (4,6) – больший потенциал вершин ребра (4,6) + меньший потенциал ребра (4,6)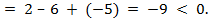 
Характеристики ребер (1,6), (2,4), (3,4), (4,6) отрицательны. Поэтому полученный план поставок не является оптимальным.
2.8.3 Улучшение плана поставок
Выбираем ребро с наименьшей отрицательной характеристикой и рисуем к нему стрелку от вершины с меньшим потенциалом к вершине с большим потенциалом. Образуется замкнутый контур из стрелок (при этом не важно, двигаемся мы по стрелкам или против них).
Определяем минимум среди поставок для стрелок этого контура, направление которых противоположно направлению новой стрелки.
Для контура поставки на стрелках в направлении новой стрелки увеличим на этот минимум, а поставки на стрелках противоположного направления уменьшим на этот минимум. Стрелка, которой соответствует выбранный минимум, ликвидируется. Поставки для стрелок вне контура остаются без изменений.
Для нового плана поставок число стрелок = число вершин 1. К этому плану поставок мы можем применить рассмотренный выше алгоритм проверки на оптимальность.
Пример 9. Характеристика ребра (1,6) 
.
Характеристика ребра (2,4)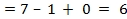 
.
Характеристика ребра (3,4) 
.
Характеристика ребра (4,6)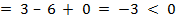 
.
У ребра (4,6) наименьшая отрицательная характеристика (−3). Рисуем к нему стрелку от вершины с меньшим потенциалом (4) к вершине с большим потенциалом (6) (см. рисунок 2.12.).
| −70 |
| −120 |
| −130 |
| −150 |
| -1 |
Рисунок 2.12 – План поставок, вариант 5
Образуется замкнутый контур из стрелок 4 – 6 – 7 – 5 – 4 (при этом не важно, двигаемся мы по стрелкам или против них). В этом контуре направление стрелок 7→6 и 4→5 противоположно направлению новой стрелки 4→6.
Определим минимум среди поставок для стрелок 7→6 и 4→5: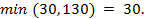 
Для контура 4 – 6 – 7 – 5 – 4 поставки на стрелках в направлении новой стрелки 4→6 (4→6 и 7→5) увеличим на этот минимум: 
и 
соответственно.
Для контура 4 – 6 – 7 – 5 – 4 поставки на стрелках 7→6 и 4→5 уменьшим на этот минимум: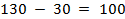 
и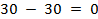 
соответственно, то есть стрелку 4→5 ликвидируем.
Поставки для стрелок вне контура остаются без изменений. Число стрелок = 6 = число вершин – 1. Получаем следующий план поставок (см. рисунок 2.13). Исследуем его на оптимальность.
| −70 |
| −120 |
| −130 |
| −150 |
| -1 |
Рисунок 2.13 – План поставок, вариант 6
Припишем вершине 1 потенциал 0 и пересчитаем потенциалы других вершин. У нас 4 ребра без стрелок: (1,6), (2,4), (3,4), (4,5). Найдем их характеристики.
Характеристика ребра (1,6) = стоимость перевозки единицы груза для ребра (1,6) – больший потенциал вершин ребра (1,6) + меньший потенциал ребра (1,6) .
Характеристика ребра (2,4) = стоимость перевозки единицы груза для ребра (2,4) – больший потенциал вершин ребра (2,4) + меньший потенциал ребра (2,4)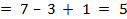 
.
Характеристика ребра (3,4) = стоимость перевозки единицы груза для ребра (3,4) – больший потенциал вершин ребра (3,4) + меньший потенциал ребра (3,4)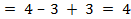 
.
Характеристика ребра (4,5) = стоимость перевозки единицы груза для ребра (4,5) – больший потенциал вершин ребра (4,5) + меньший потенциал ребра (4,5)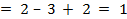 
.
Характеристика ребра (1,6) отрицательна. Поэтому полученный план поставок не является оптимальным. Рисуем к ребру (1,6) стрелку от вершины с меньшим потенциалом (1) к вершине с большим потенциалом (6) (см. рисунок 2.14.).
| −70 |
| −120 |
| −130 |
| −150 |
| -1 |
Рисунок 2.14 – План поставок, вариант 7
Образуется замкнутый контур из стрелок 1 – 6 – 7 – 5 – 1 (при этом неважно, двигаемся мы по стрелкам или против них). В этом контуре направление стрелок 7→6 и 1→5 противоположно направлению новой стрелки 1→6.
Определим минимум среди поставок для стрелок 7→6 и 1→5:
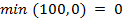. Поэтому все поставки остаются без изменений. Стрелку 1→5 ликвидируем.
Число стрелок = 6 = число вершин – 1. Получаем следующий план поставок (см. рисунок 2.15). Проверим его на оптимальность.
| −70 |
| −120 |
| −130 |
| −150 |
| -3 |
Рисунок 2.15 – План поставок, вариант 8
Убеждаемся, что нет ребер с отрицательными характеристиками, то есть это оптимальный план поставок. Затраты на перевозку равны: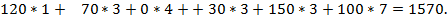 
Открытая модель
Открытая модель сводится к закрытой модели с использованием фиктивного потребителя или фиктивного поставщика.
Фиктивный потребитель
Если суммарная мощность поставщиков больше суммарного спроса потребителей, то вводится фиктивный потребитель (фиктивная вершина), которому приписывается спрос, равный разнице между суммарной мощностью поставщиков и суммарным спросом потребителей. Фиктивная вершина соединяется непосредственно со всеми поставщиками.
Стоимость перевозки единицы груза от поставщиков до фиктивного потребителя следует брать одинаковой и сравнительно большой, чтобы исключить возможности использования фиктивной вершины в качестве промежуточного пункта. Груз, предназначенный фиктивному потребителю, остается у поставщика.
Пример 10. Задана следующая транспортная сеть (см. рисунок 2.16).
| −10 |
| −40 |
| −50 |
Рисунок 2.16 – Транспортная сеть
Суммарная мощность поставщиков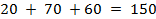 
, суммарный спрос потребителей 
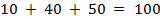. Это открытая модель.
Вводим фиктивного потребителя, которому припишем спрос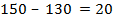 
. Это будет вершина 7. Соединим ее с вершинами 1, 3, 6 (поставщики).
Стоимость перевозки единицы груза от поставщиков до фиктивного потребителя возьмем одинаковой и сравнительно большой, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта. Например, 20. Получим следующую закрытую модель (см. рисунок 2.17.).
| −10 |
| −40 |
| −50 |
| −20 |
Рисунок 2.17 – Закрытая модель
Фиктивный поставщик
Если суммарная мощность поставщиков меньше суммарного спроса потребителей, то вводится фиктивный поставщик (фиктивная вершина), которому приписывается мощность, равная разнице между суммарным спросом потребителей и суммарной мощностью поставщиков. Фиктивная вершина соединяется непосредственно со всеми потребителями.
Стоимость перевозки единицы груза от фиктивного поставщика до потребителей следует брать одинаковой и сравнительно большой, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта. Потребитель, приписанный к фиктивному поставщику просто не получает соответствующего груза.
Пример 11. Задана следующая транспортная сеть (см. рисунок 2.18).
Суммарная мощность поставщиков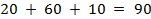 
. Суммарный спрос потребителей равен 
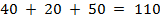. Это открытая модель.
Вводим фиктивного поставщика, которому припишем мощность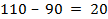 
. Это будет вершина 7. Соединим ее с вершинами 1, 3, 6 (потребители).
| −20 |
| −40 |
| −50 |
Рисунок 2.18 – Транспортная сеть
Стоимость перевозки единицы груза от фиктивного поставщика до потребителей возьмем одинаковой и сравнительно большой, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта. Например, 20. Получим следующую закрытую модель (см. рисунок 2.19).
| −20 |
| −40 |
| −50 |
Рисунок 2.19 – Закрытая модель
Задача о назначениях
Задача о назначениях является частным случаем транспортной задачи. В этом случае число поставщиков равно числу потребителей, мощность каждого поставщика и спрос каждого потребителя равны единице. Решается задача о назначениях венгерским методом. Сначала рассмотрим задачу минимизации целевой функции (экономический смысл величин исходной матрицы может быть любым).