Ковариация, корреляция случайной величины. Свойства коэффициента корреляции

Взаимосвязь переменных х и у может быть выражена одним числом. Показателями взаимосвязи переменных являются их ковариация и корреляция. Ковариация определяется по одной из следующих формул

1) Cov (x,y)=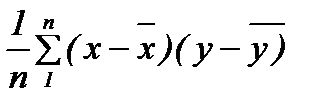

2) Cov (x, y) =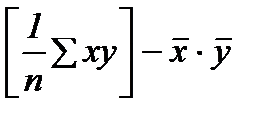

Величина показателя ковариации зависит от масштаба переменных, поэтому не является устойчивой характеристикой взаимосвязи и не подлежит смысловой интерпретации. Знак показателя ковариации указывает на направление связи: положительная величина показателя говорит о том, что связь прямая, а отрицательная – об обратной связи.

Устойчивой характеристикой взаимосвязи, то есть не зависящей от масштаба переменных, является коэффициент корреляции. В случае парной линейной зависимости переменных он определяется по формуле

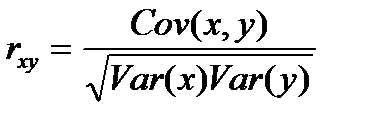
где Var 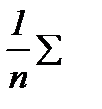(х) = (х - 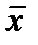)² и Var 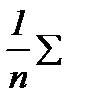(y) = (y -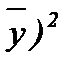

Коэффициент парной корреляции r имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у. Аналогичным образом r принимает минимальное значение -1, когда существует линейная отрицательная зависимость. Величина r =0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Промежуточные значения коэффициента корреляции интерпретируются следующим образом:

0 – 0,3 - слабая связь;

0,3 – 0,5 - умеренная связь;

0,5 – 0,7 - средняя сила связи;

0,7 – 1,0 - сильная или тесная зависимость.

Если на зависимую переменную у параллельно с фактором х оказывает влияние еще и фактор z, то коэффициент парной корреляции между у и х (r_xy) может преувеличивать или преуменьшать действительную силу связи между ними. В таких случаях частный коэффициент корреляции является более точной мерой зависимости. Его величина определяется по формуле:

,

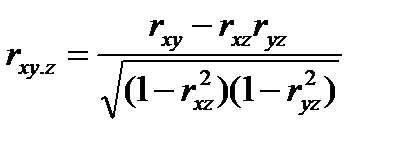где r_ху.z - коэффициент частной корреляции между х и у в случае постоянства воздействия величины z, а r_ху, r_xz и r_yz - обычные коэффициенты корреляции между х и у, между х и z, между у и z соответственно.

Квадрат коэффициента корреляции r² называется коэффициентом детерминации, он показывает долю общей вариации зависимой переменной, объясненной влиянием независимой переменой.

Свойства коэффициента корреляции r

· r изменяется в интервале от —1 до +1.

· Знак r означает, увеличивается ли одна переменная по мере того, как увеличивается другая (положительный r), или уменьшается ли одна переменная по мере того, как увеличивается другая (отрицательный r).

· Величина r величина указывает, как близко расположены точки к прямой линии. В частности, если r = +1 или r= —1, то имеется абсолютная (функциональная) корреляция по всем точкам, лежащим на линии (практически это маловероятно); если 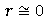, то линейной корреляции нет (хотя может быть нелинейное соотношение). Чем ближе r к крайним точкам (±1), тем больше степень линейной связи.

· Коэффициент корреляции r безразмерен, т. е. не имеет единиц измерения.

· Величина r обоснованна только в диапазоне значений x и y в выборке. Нельзя заключить, что он будет иметь ту же величину при рассмотрении значений x или y, которые значительно больше, чем их значения в выборке.

· x и y могут взаимозаменяться, не влияя на величину r ().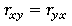

· Корреляция между x и у не обязательно означает соотношение причины и следствия.

· представляет собой долю вариабельности у, которая обусловлена линейным соотношением с x.