Проверить достоверность уравнения регрессии – значит, установить: соответствует ли математическая модель, выражающая зависимость между переменными связям в генеральной совокупности и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
Проверка достоверности уравнения в целом проводится на основе дисперсионного анализа по критерию F-Фишера.
Схема дисперсионного анализа:
1. Выдвигается рабочая гипотеза о равенстве генеральных дисперсий: дисперсии, воспроизведенной (σ2регр.) уравнением регрессии, и остаточной дисперсии (σ 2ост.), а также альтернативная ей:
Н0: σ 2регр. = σ 2ост.
Нa: σ 2регр. ¹ σ 2ост
2. Выбирается уровень значимости критерия 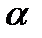 .
.
3. Производится разложение общего объема вариации:
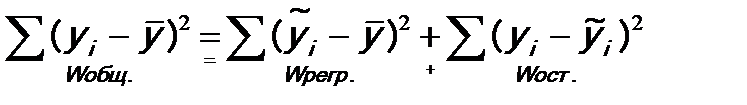
Поскольку остатки определяются как:
 ,
,
т.е. отклонения от линии регрессии по каждому наблюдению, будем обозначать остаточный объем вариации как 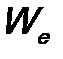 .
.
3. Определяется число степеней свободы, которое обозначается d.f. или v:
vобщ.=n-1, где n – численность выборки;
vрегр.=m (m – число параметров без условного начала). Для парной линейной регрессии vрегр.=1
vост..=n-m-1
Для парной линейной регрессии vост .= n-2.
4. Рассчитываются выборочные несмещенные оценки дисперсий:
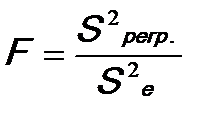
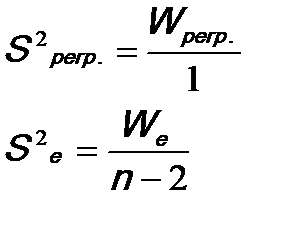
5. Определяется фактическое значение F-критерия Фишера:
6. Определяется критическое (табличное) значение критерия:
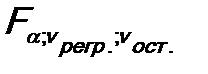
6. Делается статистический вывод:
а) Fфакт.≤ Fтабл.ÞН0 (σ2факт.= σ 2ост.)
б) Fфакт.> Fтабл.ÞНa (σ 2факт. ¹ σ 2ост)
7. Делается заключение о значимости уравнения в целом, в случае принятия альтернативной гипотезы при выбранном уровне вероятности суждения 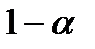 , либо – о его недостоверности, если была принята нулевая гипотеза.
, либо – о его недостоверности, если была принята нулевая гипотеза.
Если уравнение регрессии в целом значимо, то имеет смысл оценить значимость его параметров по t-критерию Стьюдента. Этот критерий применяется также для оценки значимости коэффициента парной корреляции, поскольку r – это лишь выборочная оценка генерального коэффициента корреляции 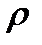 .
.
Схема t-теста:
1. Формулируются рабочая и альтернативная гипотезы:
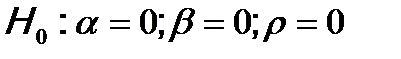
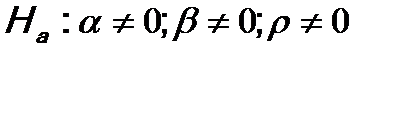
2. Выбирается уровень значимости критерия 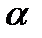 .
.
3. Рассчитываются средние ошибки выборочных характеристик:
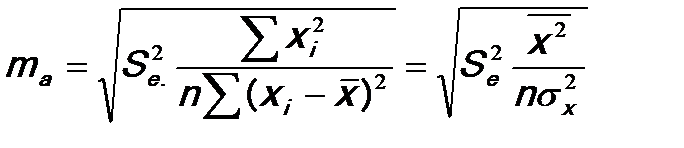 ,
,
где 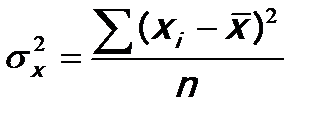 – выборочная дисперсия независимой переменной х.
– выборочная дисперсия независимой переменной х.
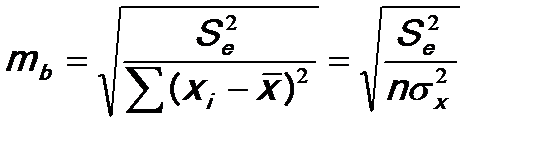
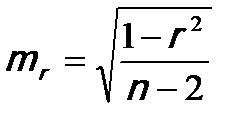
4. Определяются фактические значения t-критерия:
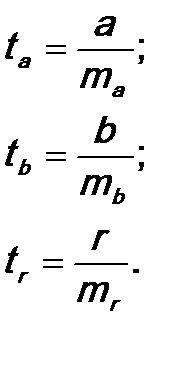
5. Определяется критическое значение:
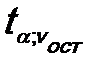 .
.
6. Фактические значения сравниваются с критическими. Тестируемые параметры будут значимыми, если:
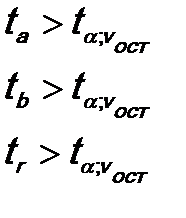
Отметим, что в парной линейной модели, поскольку в модели всего один регрессор:
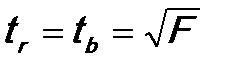 .
.
Если параметры уравнения оказались значимыми, то возможна их интерпретация и распространение выводов на генеральную совокупность.
В этом случае возможна их интервальная оценка:
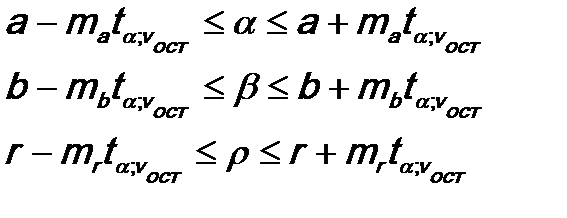
Нужно иметь ввиду, что существенные параметры регрессии не могут менять знаки на противоположные. Если нижняя граница у Вас получается отрицательной, а выборочный параметр при этом – положительный, то в качестве нижней границы следует взять ноль. Аналогично для коэффициента корреляции, к тому же нужно помнить, что он изменяется в пределах от -1 до 1, соответственно предельные границы в генеральной совокупности не могут превышать по модулю единицу.