Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах. При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица X`X особенная, так как содержит линейно зависимые векторы-столбцы, и её определитель равен нулю, т.е. нарушается предпосылка регрессионного анализа, это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели. Однако в экономических исследованиях мультиколлинеарность чаще проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица X`X в этом случае является неособенной, но её определитель очень мал. В то же время вектор оценок b и его ковариционная матрица ∑b пропорциональны обратной матрице (X`X)-1, а значит, их элементы обратно пропорциональны величине определителя |X`X|. В результате получаются значительные средние квадратические отклонения (стандартные ошибки) коэффициентов регрессии b0, b1,…,bp и оценка их значимости по t-критерию не имеет смысла, хотя в целом регрессионная модель может оказаться значимой по F-критерию. Оценки становятся очень чувствительными к незначительному изменению результатов наблюдений и объёма выборки. Уравнения регрессии в этом случае, как правило, не имеют реального смысла, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения. Существует два основных метода устранения мультиколлинарности факторов: 1.Метод дополнительных регрессий: -Строятся уравнения регрессии, которые связывают каждый из регрессоров со всеми остальными; - Вычисляются коэффициенты детерминации 
для каждого уравнения регрессии; - Проверяется статистическая гипотеза 
с помощью F-теста. Вывод: если гипотеза 
не отвергается, то данный регрессор не приводит к мультиколлинеарности. 2. Метод последовательного присоединения: - Строится регрессионная модель с учетом всех предполагаемых регрессоров. По признакам делается вывод о возможном присутствии мультиколлинеарности; - Рассчитывается матрица корреляций и выбирается регрессор, имеющий наибольшую корреляцию с выходной переменной; - К выбранному регрессору последовательно добавляются каждый из оставшихся регрессоров и вычисляются скорректированные коэффициенты детерминации для каждой из моделей. К модели присоединяется тот регрессор, который обеспечивает наибольшее значение скорректированного . Процесс присоединения регрессоров прекращается, когда значение скорректированного становится меньше достигнутого на предыдущем шаге. Каким бы образом не осуществлялся отбор факторов, уменьшение их числа приводит к улучшению обусловленности матрицы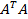 
, а, следовательно, и к повышению качества оценок параметров модели. Помимо перечисленных методов существует ещё один, более простой, дающий достаточно хорошие результаты — это метод предварительного центрирования. Суть метода сводится к тому, что перед нахождением параметров математической модели проводится центрирование исходных данных: из каждого значения в ряде данных вычитается среднее по ряду: 
. Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми