Основные предпосылки регрессионного анализа

Корреляционно-регрессионным анализом называется многообразие методов исследования параметров генеральной совокупности, распределенной по нормальному закону.

Предпосылки корреляционно-регрессионного анализа:

1) Наличие данных по достаточно большой совокупности явлений. Обычно считается, что число наблюдений должно быть в 5-6 раз, случи в 10 р., чем число факторов.

2) Качественная однородность изучаемых единиц.

3) Проверка на однородность и нормальность распределения. На однородность по коэффициенту корреляционности на нормальность по правилу трех сигм.

4) Включаемые в исследование факторы должны быть независимы друг от друга, т.к. наличие тесной связи между ними свидетельствует о том, что они характеризуют одни и те же стороны изучаемого явления и дублируют друг друга.

Корреляционный анализ позволяет с помощью выборки делать выводы о степени статистической связи между признаками.

В качестве мер связи между признаками чаще всего используется принцип ковариации и принцип сопряженности.

Принцип ковариации: наличие связи между переменными утверждается, если увеличение значения одной переменной сопровождается устойчивым увеличением или уменьшением другой переменной.

Принцип сопряженности: эта группа мер связи направлена на выяснение следующего факта – появляются ли некоторые значения одного признака одновременно с определенными значениями другого чаще, чем это можно объяснить случайным стечением обстоятельств.

Задачи корреляционно-регрессионного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценки факторов, оказывающих наибольшее влияние на результативный признак.

Изучение корреляционной связи имеет 2 цели:

1) Измерение параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной;

2) Измерение тесноты связи двух или большего числа признаков между собой.

Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К.Ф.Гауссом (1777-1855), а был предложен Лежандром. В простейшем случае он формулируется так: Результат yi повторяющихся измерений можно рассматривать как сумму неизвестной величины x и ошибки измерения ej:

3) Прочие задачи корреляционно-регрессионного анализа (КРА):

3.1 Выделение важнейших факторов, влияющих на результативный признак. Эта задача решается на базе мер тесноты связи факторов с результативным признаком.

3.2 Оценка эффективности использования факторов производства.

3.3 Прогнозирование возможных значений результативного признака при задаваемых значениях факторных признаков.

3.4 Подготовка исходных данных для решения оптимизационных задач. Например, для нахождения оптимальной структуры производства на основании корреляционно-регрессионной модели, Определяются показатели производительности труда, интенсивности расхода сырьевых, финансовых ресурсов и т.п.

К основным задачам корреляционно–регрессионного анализа в области моделирования экономики можно отнести следующие.

• Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа. Данную проблему принято называть проблемой спецификации.

• Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным. Это так называемый этап параметризации.

• Проверка качества найденных параметров модели и самой модели в целом. Иногда этот этап анализа называют этапом верификации.

• Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.

Как видно, из вышесказанного, корреляционно–регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Особую ценность этот метод приобрел после появления ЭВМ, тат как математические процедуры такого анализа довольно легко стало реализовывать в виде алгоритмов и программ статистической обработки данных.

10. Регрессионный анализ устанавливает форму зависимости между случайной величиной и значения переменной величины, причем, значения считаются точно заданными.

Уравнение регрессии – это формула статистической связи между переменными.

Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией (нескольких переменных – множественной).

Выбор формулы зависимости называется спецификацией уравнения регрессии. Оценка значений параметров выбранной формулы называется параметризацией.

В основе оценки параметров линейной регрессии лежит Метод Наименьших Квадратов (МНК) – это метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

Функция Q является квадратичной функцией двух параметров a и b. Т.к. она непрерывна, выпукла и ограничена снизу (), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b:

.

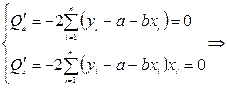
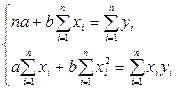Разделив оба уравнения системы на n, получим:

или

Иначе можно записать:

и - средние квадратические отклонения значений тех же признаков.

Т.о. линия регрессии проходит через точку со средними значениями х и у , а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции.

Если кроме регрессии Y на X для тех же эмпирических значений найдено уравнение регрессии X на Y (, где ), то произведение коэффициентов:

.

квадратические отклонения значений тех же признаков.
Коэффициент регрессии - это величина, показывающая, на сколько единиц размерности изменится величина при изменении величины на одну единицу ее размерности. Аналогично определяется коэффициент .

Как и коэффициент корреляции, коэффициент регрессии может принимать и положительные и отрицательные значения. Например, если коэффициент имеет знак "-", то это означает, что при увеличении значения признака на единицу его размерности значение признака уменьшается на величину, равную .

Уравнения линейной регрессии являются уравнениями прямых линий в плоскости, проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.

Для того, чтобы полученные МНК оценки обладали желательными свойствами, сделаем следующие предпосылки об отклонениях:

1) величина является случайной переменной;

2) математическое ожидание равно нулю: ;

3) значения независимы между собой. Откуда вытекает, в частности, что

4) дисперсия постоянна:;

5) ошибки подчиняются нормальному распределению ~ (это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов).

Если условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:

1. Оценки являются несмещёнными (т.е. математическое ожидание каждого параметра равно его истинному значению ).

2. Оценки состоятельны (дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: ). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к , а b близко к .

3. Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин .

11. Оценка значимости уравнения регрессии в целом и его параметров

После того как найдено уравнение регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

. (2.12)

где - индивидуальная ошибка аппроксимации.

Если - модель отличного качества; если - модель хорошего качества; если - удовлетворительная модель; если - необходимо строить другую модель.

Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной от среднего значения раскладывается на две части – «объясненную» и «необъясненную»:

,

где – общая сумма квадратов отклонений;

– факторная сумма квадратов отклонений (сумма квадратов отклонений, объясненная регрессией);

– остаточная сумма квадратов отклонений