II.3. Задачи к теоретической карте №2

№ 1.

1. Дано: а || в. Найти: х.	3. В Дано: КР || DE. Найти: х. К Р
4.

Рис. 41

 

№2. В параллелограмме ABCD точки К и F – середины сторон ВС и АD соответственно. Доказать, что отрезки АК и СF делят диагональ параллелограмма BD на три равные части.

 

План доказательства.

1. ВМ=МN.

2. MN=ND.

3. BM=MN=ND.

Используемые факты из теоретической

карты: 1.

 

№3. Высота CDтреугольника АВС делит медиану BM в отношении 3:1, считая от вершины В. В каком отношении CD делит сторону АВ, считая от вершиныА?

 

План решения.

Проведем MK || DC.

1. .

2. DK=AK.

3.

Ответ: 2:3.

Используемые факты из теоретической карты: 1.

№4. Длина основания АС треугольника АВС равна 3, а медиана AD равна 4. Высота BE делит медиану AD пополам. Найти площадь треугольника АВС.

План решения.

1. Дополнительное построение: DК || ВE.

2. AК. 3. DK. 4. ВЕ. 5. S_∆ABC.

Ответ: .

 

Используемые факты из теоретической карты: 1.

№5. На сторонах AD и CD параллелограмма ABCD взяты точки M и N так, что MN||AC. Доказать, что площади треугольников ABM и CBN равны.

План доказательства.

1. .

2. .

3.

4. AD·NC=AM·DC

5. ВС∙NC= AM∙АВ

6. S_∆ABM = S_∆CBN.

Используемые факты из теоретической карты: 1.

№6. Точки M и P – середины смежных сторон AD и DC параллелограмма ABCD. MC и PB пересекаются в точке K. Найти BK: KP.

План решения.

1. Дополнительные построения:

BS||CM, PS||BC.

2. NP=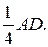

3. SN=BC=AD.

Рис. 46 4. SN: NP.

5. BK: KP= SN: NP.

Ответ: 4:1.

Используемые факты из теоретической карты: 1.

№7. В треугольнике АВСстороны АВи ВС равны и 6 соответственно. Точка D лежит на стороне АС, угол DBC равен 45⁰, угол ABD равен 60⁰.
CM – медиана, пересекающая BD в точке O. В каком отношении точка O делит BD?

План решения.

1. Дополнительное построение: DP||СM.

2. (используя теорему синусов для

треугольников BDC и ABD).

3. 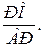4.

Ответ: 1:3.

Используемые факты из теоретической карты: 1.

№ 8. В треугольнике АВС АВ = АС = 75. ВС = 90. Вершины В и С соединены с серединой О высоты, проведённой из вершины А. ВО и СО пересекают стороны АС и АВ соответственно в точках В₁ и С₁. Найти площадь четырёхугольника ОС₁АВ₁.

 

План решения.

1. АК. 2. АО. 3. Провести КК₁ || ВВ₁.

4. АВ₁= 5. С₁В₁ || ВС.

6. DС₁АВ₁~ D ВАС,

7. С₁В₁. 8.

Ответ: 450.

Используемые факты из теоретической карты: 1.

№9. В первой печатной книге по геометрии на русском языке «Приемы циркуля и линейки (1708 и 1709 гг.)» дано следующее построение: «Для разделения отрезка АВ на пять равных частей строим на нем равносторонний треугольник ASB, от вершины S откладываем на стороне AS, пять равных отрезков произвольной длины: 5· n = SC.

Через точку С проводим прямую, параллельную АВ и пересекающую SB в точке D. Затем на CD откладываем пять отрезков, равных n. Через полученные точки проводим лучи с началом в точке S. Доказать, что отрезок АВ разделится лучами на 5 равных частей.

Указание: равенство следует из утверждения 2 теоретической карты.

№ 10. Доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения боковых сторон, делит основания трапеции пополам.

 

План доказательства.

1.

2.

3. BM=MC, AN=ND.

 

Используемые факты из теоретической

карты: 1, 2.

№11. Один из катетов прямоугольного треугольника равен 15, а проекция
другого катета на гипотенузу равна 16. Найти площадь треугольника.

 

План решения.

1. AD.

2. CD.

3. S_∆АВС.

Ответ: 150.

Рис. 51

Используемые факты из теоретической карты: 3.2; 3.1.

№12. Окружность, построенная на катете прямоугольного треугольника как на диаметре, делит гипотенузу в отношении 1:3. Найти углы треугольника.

План решения.

1. ÐСDВ = 90⁰.

2. СD (в частях).

3. ,

4. В.

Ответ: 60⁰, 30⁰, 90⁰.

Используемые факты из теоретической карты: 3.1.

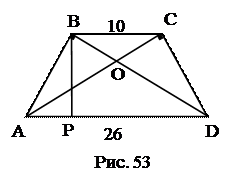
№ 13. Определить площадь равнобедренной трапеции, у которой основания 10 и 26, а диагонали перпендикулярны боковым сторонам.

План решения.

1. АР.

2. PD.

3. ВР.

4. S_ABCD.

Ответ: 216.

Используемые факты из теоретической карты: 3.1.

14. Перпендикуляр, опущенный из вершины тупого угла ромба на его сторону, делит большую диагональ на отрезки, равные 3,5 и 12,5. Определить сторону и меньшую диагональ ромба.

План решения.

1. АС, АО, КО.

2. FP=PD.

3. AF: FP: PD.

4.Выразить АР через АD.

5. АD.

6.DО, ВD.

Используемые факты из теоретической карты: 1; 3.3.

№ 15. В прямоугольном треугольнике АВС (ÐС=90°) проведена медиана АА₁, пересекающая высоту треугольника CD в точке М. Найти отношение

СМ: MD, если ÐА=a.

Дополнительное построение:

DD₁|| AA₁.

План решения.

1.

2.

3.

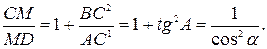
Ответ:

Используемые факты из теоретической карты: 1; 3.4.

III. ОКРУЖНОСТЬ